Andrei Markov matematikariak liburu bateko bokalak eta kontsonanteak zenbatu zituen. Lortutako emaitzak erabiliz, Markov Kateak existitzen direla frogatu zuen. Modu errazean azal daiteke bere arrazonamendua eta hori da hain zuzen artikulu honetan ikusiko duguna.
Markov Kateak gertakizun estatistikoak aztertzeko erabiltzen dira. Oso tresna boteretsuak dira eta, hori dela kausa, gaur egun hainbat arlotan erabiltzen dira: adimen artifizialeko sistemetan, supermerkatuko ilaretan, ospitaletako larrialdietako zerbitzuetan, etab. Markov Kateak orain dela ehun urte baino gehiago aztertu ziren lehen aldiz.
Badakigu estatistikan badaudela gertakizun batzuk elkarrekin independenteak direnak. Hau da, une honetan gertatzen denak ez du harremanik lehenago gertatutakoarekin. Independentzia hau gertatzen da, esate baterako, txanpon bat airera botatzen dugunean eta aurpegia edo gurutzea ateratzen den ikustean. Alegia, aurpegia ateratzeko probabilitatea 1/2 da (trukatu gabeko txanpona bada, noski), hots, aurreko jaurtiketen emaitzekiko independentea da. Dadoetan ere hala gertatzen da, eta dadoen jaurtiketak independenteak direla esaten dugu.
Gaur egun badakigu ordea gertakizun guztiak ez direla elkarrekin independenteak, hots, orain gertatzen dena lehenago gertatutakoaren araberakoa izan daitekeela. Adibidez, gaur dudan lan atzeratuaren tamaina atzo egindako lanaren araberakoa da ; atzo lan asko egin banuen gaur lan atzeratu gutxiago dut baina Markoven garaian, berriz, estatistikan aztertzen ziren gertakizun guztiak independenteak zirela uste zuten.
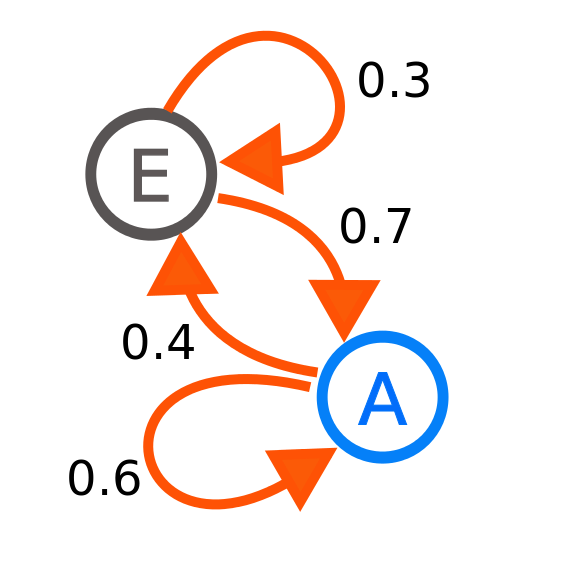
Uste hori okerrekoa zela frogatzeko, Andrei Markov matematikariak Alexander S. Pushkin idazlearen Eugene Onegin olerki-liburua erabili zuen. Olerki horretako 200 zati aukeratu zituen eta zati bakoitzak 100 letra zituen. Lehenik, bokal eta kontsonante kopurua zenbatu zuen eta, horrela, 7.788 bokal eta 12.212 kontsonante zeudela ikusi zuen. Beraz, probabilitate-teoria erabiliz, ondoriozta daiteke olerki horretako letra bat bokala dela 0.3894 probabilitatearekin eta kontsonantea 0.6206 probabilitatearekin.

Ikerketa honen bigarren pausoan, Markovek olerki horretako hurrengo gertakizunak zenbatu zituen: (i) bi bokal jarraian, (ii) bi kontsonante jarraian, (iii) kontsonante bat bokal baten ondoren eta (iv) bokal bat kontsonante baten ondoren. Haren emaitzen arabera, bi bokal jarraian 1.365 aldiz agertu ziren, kontsonante bat bokal baten ondoren eta bokal bat kontsonante baten ondoren 6.423 aldiz, eta bi kontsonante jarraian 5.788 aldiz.
Aurreko paragrafoan esandakoan aurrera eginez, olerki horretan bi bokal jarraian agertzeko probabilitatea 0.06825 da. Alabaina, garai hartako matematikariek uste zuten gertakizun guztiak independenteak direla eta, hori horrela balitz, bi bokal jarraian agertzeko probabilitatea 0.3894*0.3894 izan beharko litzateke. Kalkulagailua erabiliz, argi ikus daiteke bi zenbakiak ezberdinak direla, eta horregatik, garai hartako matematikak oker zeudela. Ikerketa honi esker, beraz, probabilitate teoriaren adar berri bat sortu zen, Makov Kateen teoria alegia.
Literatura eta matematika harreman estuko zientziak dira. Artikulu honetan Markov Kateen aurkikuntza azaldu dugu. Hala ere, beste harreman mota asko dauzkate matematikak eta literaturak elkarrekin, baino hurrengo batean emango dizuet horren berri.
Egileaz: Josu Doncel Matematikan doktorea da eta egun, INRIA Institutuan dihardu ikertzen.