Hegazkin supersonikoek eragindako soinu-eztanda sortzen den unetik lurrerainoko hedapena zehatz-mehatz simulatzea ez da gai erraza. Ereduaren denbora-tarte handietarako propietateak babesten dituzten zenbakizko metodoak behar dira, soluzioaren hurbilketen eraginkortasuna manten dadin. Zenbakizko biskositateak zeresan handia du horretan.

2003. urtean, Concorde hegazkin supersonikoak azken aldiz egin zuen New York eta Londres arteko bidaia. Istripuak eta arazo ekonomikoak zirela medio, bere erabilera eten egin zen. Baina beste kausa batek ere influentzia handia izan zuen erabaki hartan. Izan ere, ontzi horiek, soinuaren abiadura gainditzean, atmosferan presio-perturbazio itzela sortarazten dute, airearen lekualdatzeak eta euste aerodinamikoak eraginda. Fenomeno hori bi danbada jarrai balira bezala antzematen dugu eta, bai gizakiontzat, bai eraikinentzat, oso kaltegarria izan daiteke.
Hortaz, azken hamarkadetan aeronautika-ikerketan izandako ardurarik handienetariko bat zarata hori kontrolatzea eta murriztea izan da, hori baita garraio zibil supersonikoak berriz garatu ahal izateko giltzetako bat. SSBD proiektuak hegazkinen forma eraldatuz helburu hori lortzea posible dela ziurtatu zuen. Hala eta guztiz ere, gainontzeko frogek neurrigabeko kostua izan ez dezaten, beste erremintak behar dira, zenbakizko analisian oinarritutako simulazio konputazionala nagusia izanik.
Soinu-eztandaren hedapenaren ereduen artean, Burgersen ekuazio handitua hartu ohi da. Horrek atmosferaren presio-banaketaren perturbazioa, hedapenaren distantzia eta perturbazioaren iraupena erlazionatzen ditu. Izpi-hodiaren azalera eta atmosferako beste zenbait baldintza (hain zuzen ere, dentsitatea, soinuaren abiadura, termo-biskositatea eta lasaikuntza molekularrak) ere kontuan hartzen dira.
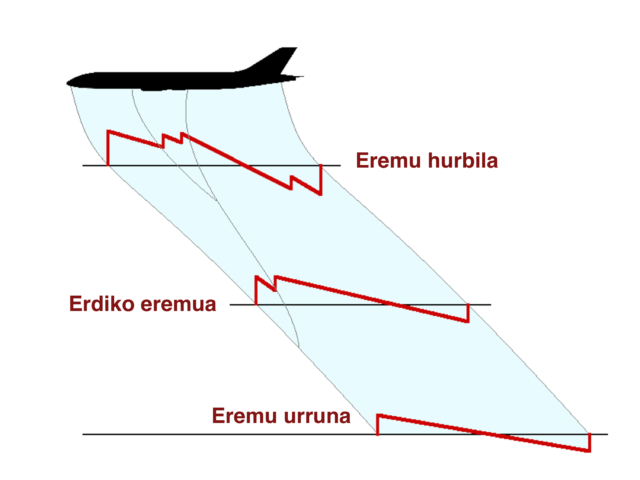
Esparru horretan, beraz, badakigu hegazkinak sortzen duen (eta neur daitekeen) soinu-sinadura teorikoki nola hedatzen den atmosferatik. Ezaguna da ere hain kaltegarriak ez diren uhinen itxura.
Beraz, honetan datza soinu-eztandaren minimizazioaren problema: hegaldiaren altitudea eta lurzoruan lortu nahi den soinu-sinadura emanik, hobeto erreproduzitzen duen hegazkinaren eremu hurbileko soinu-sinadura berreskuratu.
Kontuan izan behar da denbora-eskalak oso ezberdinak direla: presioaren perturbazioa segundoerdi baino gutxiago batean gertatzen den bitartean, uhinaren hedapenak ia minutu oso bat iraun
dezake. Horregatik, tratamendu konputazionalerako zenbakizko eskemak denbora-tarte luzeetan ondo portatzea ezinbestekoa da.
Problema mota horietan agertzen diren arazoen errudun nagusia biskositatea da. Burgersen ekuazio handituaren ez-linealtasunak, presioaren gorabeherak pilatuz, jauzi handiak sortzen ditu soluzioan. Hauek ondo kudeatu ahal izateko, zenbakizko biskositatea erabiltzea ezinbestekoa da. Baina, gehiegi erabiliz gero, soluzioaren denbora-tarte luzeko portaera guztiz aldatzen da. Horretan datza, beraz, biskositatearen madarikazioa: beharrezkoa da soluzioaren jauziak ondo hurbiltzeko baina, aldi berean, soluzioaren propietate garrantzitsu bat aldatzen du.
Arazo hori ez da ahuntzaren gauerdiko eztula. Izan ere, optimizazio arazoetan eragin handia izan dezake. Batzuetan begi-bistakoak izango dira ondorioak (oszilazioak soluzioan, adibidez), baina beste askotan (konbergentzia abiaduran, esate baterako) normala dirudien portaera baten atzean ezkutaturik egongo dira. Artikuluan zehar, egoera horiek ekiditzeko gakoak ematen ditugu.
Artikuluaren fitxa
- Aldizkaria: Ekaia
- Zenbakia: Ale berezia. 2018
- Artikuluaren izena: Hegazkin supersonikoak eta biskositatearen madarikazioa.
- Laburpena: Hegazkin supersonikoek eragindako soinu-eztandaren hedapena eremu hurbiletik lurreraino zehatz-mehatz simulatzea ez da erraza. Ereduaren denbora-tarte handietarako propietateak babesten dituzten zenbakizko metodoak behar dira. Artikulu honetan, soinu-eztandaren minimizazioarekin erlazionaturik dagoen optimizazio eta alderantzizko diseinu-problema ikertu dugu. Bereziki, bere soluzioaren hurbilketen eraginkortasuna mantentzeko gakoak ematen ditugu.
- Egilea: Alejandro Pozo Pazos
- Argitaletxea: UPV/EHUko argitalpen zerbitzua
- ISSN: 0214-9001
- Orrialdeak: 21-36
- DOI: 10.1387/ekaia.17898
Egileaz
BCAM-Basque Center for Applied Mathematics zentroan landu de tesia Alejandro Pozo Pazosek.
Ekaia aldizkariarekin lankidetzan egindako atala.
