Landu dugun problemaren motibazioa bizitza errealeko egoera batzuekin erlazionatuta dago. Azal dezagun gaur egungo horietakoren bat. Txartelen erabilera gero eta hedatuago dago, hoteleko logelen ateak irekitzeko, autobideen bidesarietan, garraiobide batzuetan edo parkimetroetan ordaintzeko, besteak beste.

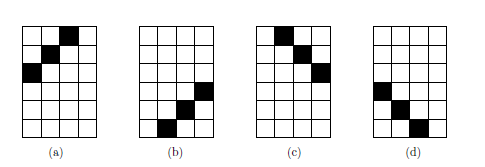
Imajina dezagun autoa aparkaleku batera sartzeko lauki sareko txartela diseinatu nahi dugula. Txartela, parkimetroan sartzea errazteko asmoz, edozein posiziotan sartzeko aukera posible izango da, parkimetroaren zirrikituaren neurria (r laukietako luzerakoa) kontuan izanik. Hau da, txartela laukizuzena bada lau aukera dugu era arrakastatsuan sartzeko, 2. irudiaren adibidean ikusten den bezala. Bi txartel berdinak dira, batetik (a) bestera pasatu ahal bada 180 gradu biratuz (b), aurrealdetik atzealdera itzulia emanez (c) edo bien konbinaketa eginez (d). Erantzun nahi ditugun galderak mota honetakoak dira: zenbat txartel desberdin egin liteke bi kolore erabiliz? Eta zehatz-mehatz hiru lauki beltzez eta gainontzeko laukiak zuriz margozten badira? Eta kolore gehiago erabiliz? Eta txartela karratuak kontsideratzekotan?
Problema modelizatzeko nahian, txartelak matrize moduan ikusiko ditugu. Izan bitez r, s eta t zenbaki arruntak. Orduan, gure lanaren interesa t kolore erabiliz r x s tamainako matrize ez-baliokideak zenbatzean datza. Kopuru horiek matrize orokorren kasuan a(r; s; t) notazioarekin adieraziko ditugu. Bi matrize baliokide direla esango dugu baldin eta berdinak badira islapenak (horizontalak zein bertikalak) edo biraketak (180 gradukoen multiploak laukizuzenen kasuan) egin ondoren. Emaitzak r eta s neurrien bikoitasunaren menpekoak izango dira.
Lan honen jatorria EKAIA 26 eta 27 aldizkarietan agertutako [1, 2] artikuluak dira. Lehenengoan, Konputazioa erabiliz formula batzuk induzitzen dira; bigarrenean, oinarrizko Konbinatoria erabiliz aieru batzuen froga matematikoa erakusten da. Hirugarren honetan Pólyaren zenbatzeko teoria aplikatuko da formulak lortzeko eta orokorpenak egiteko.
Aipatutako lanetan, patroi bitarrak landu dira, hots, bi koloredun matrizeen kalkulua. Matrize orokorren kasuan, (1) adierazpenean formulen laburpena dugu.
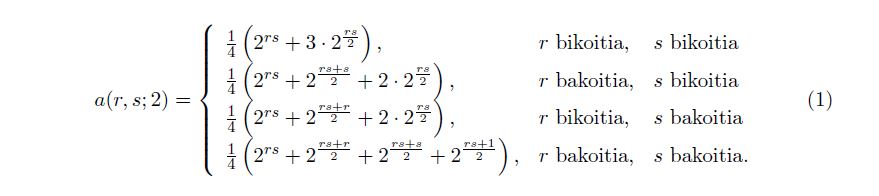
Aurreko emaitzak behin berriro frogatzeaz gain, teoriari esker formula horiek orokortuko ditugu bi norabidetan: (i) patroi bitarrak erabiltzetik t koloredun patroi ez baliokide kopurua kalkulatzera; eta (ii) kolore bakoitzaren maiztasuna jakinik, patroi ez-baliokide kopurua lortzeko bidea emanez. [3] lanean azalduko diren emaitzetan oinarrituta, hogeita hamar segida onartuak izan dira The On-Line Encyclopedia of Integer Sequences (OEIS) webgunean. OEIS zenbaki arrunten, zatikien, zenbaki transzendenteen digituak eta zenbaki konplexuen segidak dituen entziklopedia on-line da, [4] estekan kontsulta daitekeena. Neil James Alexander Sloane matematikaria 1960 urteetan biltzen hasi zen eta 2018an 300,000 segida inguru ditu, mota honetako datu-base handiena izanik.
Erreferentziak
[1] YURRAMENDI Y. 2013. \Matematika esperimentalaren adibide bat: Lauki sareko patroi bitarren kopuruaren kalkulua,” EKAIA, 26, 325{348.
[2] MERINO M. eta YURRAMENDI Y. 2014. \Lauki sareko patroi bitarren kalkulua, oinarrizko konbinatoriaren eskutik,” EKAIA, 27, 237{262.2
[3] MERINO M. eta UNANUE I. 2018. \Lauki sareko patroien kalkulua, P_olyaren teoriaren eskutik,” EKAIA, 34, onartua.
[4] SLOANE N.J.A. (ed.), \The On-Line Encyclopedia of Integer Sequences.” Website, eguneratze-data: 2017-05-12. http://oeis.org
Artikuluaren fitxa
- Aldizkaria: Ekaia
- Zenbakia: Ekaia 34
- Artikuluaren izena: Lauki sareko patroien kalkulua, Pólyaren teoriaren eskutik.
- Laburpena: Lan hau Yurramendiren (2013) eta Merino eta Yurramendiren (2014) artikuluen jarraipena da. Horietan, formula matematiko batzuk eman ziren kalkulatzeko zenbat patroi bitar ez-baliokide diren lauki-sarean. Lan honen helburua formula matematiko horiek eta haien orokorpenak Burnside eta Pólyaren zenbatzeko teoriaren bidez azaltzea da. Izan ere, bi kolore baino gehiago duten patroiak zenbatuko ditugu eta, gainera, kolore guztien maiztasuna jakinda, patroi ez-baliokideen kopurua lortzeko bidea emango dugu. Artikulu hau UPV/EHUko Imanol Unanue Gualen Matematikako Gradu Amaierako Lanean oinarrituta dago.
- Egileak: María Merino Maestre, Imanol Unanue Gual.
- Argitaletxea: UPV/EHUko argitalpen zerbitzua.
- ISSN: 0214-9001
- Orrialdeak: 289-316
- DOI: 10.1387/ekaia.17851
Egileez
María Merino Maestre, Imanol Unanue Gual UPV/EHUko Zientzia eta Teknologia Fakultateko Matematika Aplikatua eta Estatistika eta Ikerkuntza Operatiboa sailean dabiltza.
Ekaia aldizkariarekin lankidetzan egindako atala.