Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta aurten ere, hamar urte betetzen dituen ohiturarekin jarraituz, udako oporretan egiteko ostiralero matematika-ariketa bat izango duzue. Javier Duoandikoetxea matematikariak guztira sei ariketa aukeratu ditu Zientzia Kaieran argitaratzeko.
Hona hemen gure bigarren ariketa:
Irudiko laukizuzenaren alde luzeak 25 cm du eta karratuaren aldeak, 20 cm. Zein da laukizuzenaren alde txikiaren luzera?
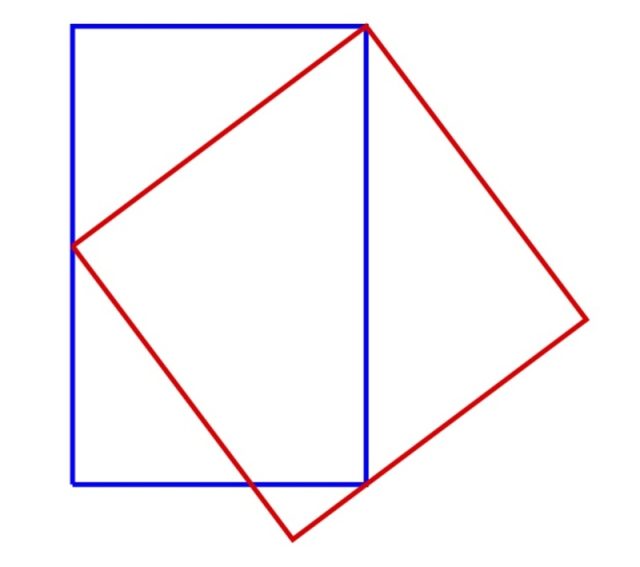
Zein da erantzuna? Idatzi emaitza iruzkinen atalean (artikuluaren behealdean daukazu) eta, nahi izanez gero, zehaztu jarraitu duzun ebazpidea ere. Irailean emaitza zuzenaren berri emango dizugu.
Ariketak “Calendrier Mathématique 2025” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.
3 iruzkinak
Oraingoan ere, emaitza emanez hasiko naiz: laukizuzenaren alde txikia 16 cm da.
Ebazpenean Pitagoras eta Tales handien teoremak erabiliko ditut, bata edo bestea aplikatuz 4 triangelu angeluzuzenetan. Triangeluetan batetik bestera jauzi egingo dut erlojuaren orratzen norantzari jarraituz betiere.
Lehen triangelua irudiari begiratuta laukizuzenaren kanpoan ageri da, eskuman, eta triangelu angeluzuzena da.
Bertan hipotenusa (25 cm) eta kateto handia (20 cm) ezagunak dira; beraz, Pitagorasen laguntzarekin erraz kalkulatuko dugu beste katetoaren neurria.
400+kat^2 = 625 → Lehen triangeluan 15 cm da kateto txikia.
Egin dezagun jauzi bigarren triangelura; laukizuzenaren kanpoan dago, beheko aldean, txikia eta angeluzuena da.
Bertan, kateto handia 20-15 = 5 cm da.
Lehen bi triangeluak antzekoak direnez, Talesek lagunduko digu.
5/20 = hip/25 → Bigarren triangeluan 6,25 cm da hipotenusa.
Berriro proportzionaltasuna erabiliz, 5/20 = kat/15 → Bigarren triangeluan kateto txikia 3,75 cm luze da.
Triangelu txikitik ezkerrera jo eta laukizuzenaren barruan topatuko dugu hirugarren triangelua, angeluzuzena.
Horretan 20-3,75 = 16,25 cm da hipotenusa.
Bigarren eta hirugarren triangeleuak ere antzekoak dira; beraz Talesen teorema aplikatuko dugu.
16,25/6,25 = kat/5 → Hirugarren triangeluan 13 cm da kateto handia (bertikala).
Azkenik, gora joko dugu laugarren triangelura jauzi eginez. Horretan 25-13 = 12 cm da kateto bertikala.
Gainera, ezaguna da laugarren triangeluko hipotenusa, hots, karratuaren aldea: 20 cm.
Bukatzeko, beraz, PItagorasen teorema aplikatuko dugu:
144+kat^2 = 400 → Laugarren triangeluaren kateto handia 16 cm da; laukizuzenaren aldea txikia, alegia.
Buelta batzu eman diot, galdu egin naiz eta triangelu ekibalente asko zeudela ikusi, ez diot ebazpena ikusi eta utzi egin dut. Gerora ikusi dut ba zegoela triangelu bat non hiru datu ezagutzen nintuen, laukiaren alde luzea (25) kateto bat (20) eta ángelu bat. Honela honako hiruko erregla ebatzi dut (20/25=20/x) non x=16. Hau da nire ebazpena.
Laukizuzenaren eta karratuaren erpinak izendatuko dtut:
laukizuzenaren erpinak ABCD, (goiko ezkerrekoa A eta erlojuaren orratzen alde biratuz B, C eta D).
Karratuaren erpinak A’, B’, C’ eta D’ (A’ erpina AD aldean eta B’=B).
Paralelotasuna // eran izendatuko da.
Zera ikusten da:
1) BC’C triangelua zuzenean BC’ katetoa 20 cm eta BC hipotenusa 25 cm. Pitagorasen teoremaz, CC’ katetoa 15 cm
2) AD // BC eta A’D’ // B’C’ direnez, Â’ angelua=C angelua; beraz, A’AB eta CC`B triangelu zuzen antzekoak dira, eta, ondorioz, aldeak proportzionalak:
AB/A’B’ = C’B’/CB —> AB/20 = 20/25 = 4/5 = 16/20 —> AB = 16 cm laukizuzenaren alde txikia.
Hurrengora arte!!