Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta aurten ere, udako oporretan egiteko asteazkenero ariketa matematiko bat izango duzue, Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.
Hona hemen gure bigarren ariketa:
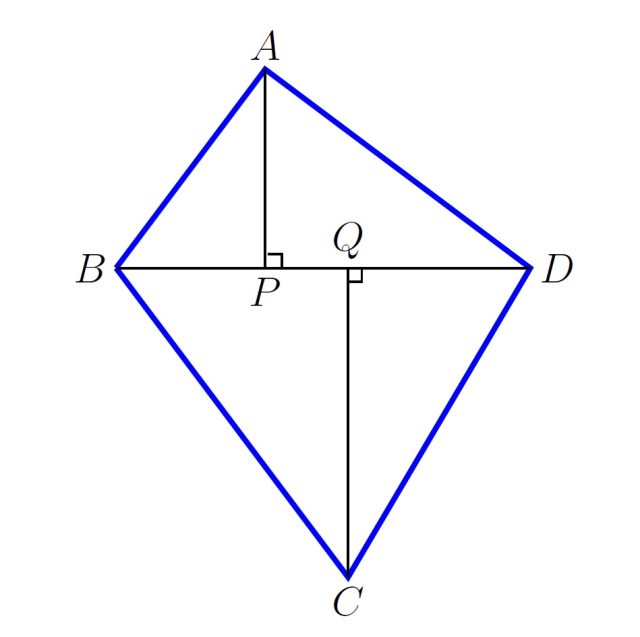
Irudiko zuzenki batzuen neurriak hauek dira: AB = 9 cm, BC = 14 cm, CD = 13 cm, DA = 12 cm eta BD = 15 cm. Zein da PQ zuzenkiaren neurria?
Zein da erantzuna? Idatzi emaitza iruzkinen atalean (artikuluaren behealdean daukazu) eta, nahi izanez gero, zehaztu jarraitu duzun ebazpidea ere. Irailean emaitza zuzenaren berri emango dizugu.
Ariketak “Calendrier Mathématique 2024. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.
4 iruzkinak
Arratxalde on;
Eman dezagun BQ=a, QD=b, eta BP=c, eta PD=d
Orduan plantea dezakegu, alde batetik;
a+b=15—>a=15-b
a^2+h^2=14^2 (non h BCD hirukiaren altura den)
b^2+h^2=13^2
Despejatuz ateratzen zait; a=8.4 eta b=6.6
Beste aldetik, BAD hirukia kontuan hartuz;
c+d=15—>c=15-d
c^2+h_2^2=9^2 —>(non h_2 BAD hirukiaren altura den)
d^2+h_2^2=12^2
Despejatuz ateratzen zaidana; d=9.6 eta c=5.4
Eskatzen zaigun balorea R=a-c da, berez, R=8.4-5,4=3 metro.
Behintzat horrela ebatzi dut nik.
Besteen erantzunen zai geratzen naiz.
Mila esker ariketarengatik.
Kaixo!
Problema hau ebazteko nire arrozamendua honakoa izan da: PQ kalkulatzeko, beharrezkoa da BD eta BP kalkulatzea. Horiek Pitagorasen teoremarekin kalkula daitezke PA eta QC kalkulatuta, ABD eta BCD hirukien altuerak direnak, hurrenez hurren. Altuerak kalkulatzeko azalera erabili dut, zeina perimetroarekin kalkulatu dut.
Hortaz,
ABD
2p=9+15+12
p=18
A= √(18*(18-9)*(18-15)*(18-12))=54
h=54*2/15=7,2=PA
BCD
2p=14+13+15
p=21
A= √(21*(21-14)*(21-13)*(21-15))=84
h=84*2/15=11,2=QC
AB^2=BP^2+PA^2
81=BP^2+51,84
BP=5,4
CD^2=QC^2+QD^2
169=125,44+ QD^2
QD=6,6
BD=BP+PQ+QD
PQ=BD-BP-QD=15-5,4-6,6=3
3 da PQ zuzenkiaren neurria.
Ondo segi!
Problema geometriko hau ebazteko, BD zuzenkiaren gainean dauden triangelu zuzenak erabili ditut, altuera komuna dutenak, hain zuzen ere.
Bietan Pitagorasen teorema erabiliz:
BP^2+PA^2=81
(15-BP)^2+PA^2=144
Bigaren ekuazioa garatuz eta lehenengoa bertan ordezkatuz, honako berdintza hau lortuko dugu:
162=30•BP → BP=5,4cm
Prozedura bera erabiliz, BD zuzenkiaren azpiko triangelu zuzenetan ere Pitagoras aplikatuz:
QD^2+QC^2=169
(15-QD)^2+QC^2=196
Eta sistema ebazteko lehen ekuazioaren balioa bigarren ekuazioan ordezkatuz, modu errazean lortuko dugu berdintza hau:
198=30•QD → QD=6,6cm
Azkenik, PQ=15-BP-QD
Beraz, PQ=3cm
Kaixo!
Triangeluen antzekotasuna eta Pitagorasen teorema erabilita, hona hemen nire proposamena:
BAD triangelua zuzena da, (9,12,15) terna pitagorikoa baita (81 + 144 = 225); zati hiru eginez, (3,4,5), angelu zuzenak eraikitzeko egiptoarrek erabilitako triangelua dugu: 9 + 16 = 25 (honi esker, konturatu naiz BAD triangelua zuzena dela).
Angelu zuzena A erpinean dago, bertatik BD aldeari dagokion altuera marrazten bada, antzekoak diren hiru triangelu zuzen izango ditugu: BAD, BPA’ eta A”PD, non A = A’+ A”, B = A”, D = A’ eta P = A = 90 diren.
Hiru triangelu hauen barneko angeluak berdinak dira, ondorioz, antzekoak; hau da, alde homologoak proportzonalak.
Antzekotasuna BAD eta A”PD triangeluetan aplikatuta, aldeak proportzionalak direnez, zera dugu:
PD/AD = A”D/BD –> PD/12 = 12/15 –> PD = 9,6 cm
Jarraian, BQC eta CQD triangelu zuzenetan Pitagorasen teorema erabiliz, QD kalkulatuko da. QC katetoa partekatzen dutenez:
14^2 -BQ^2 = 13^2 – QD^2
196 -(15 – QD)^2 = 169 – QD^2
196 -225 + 30QD -QD^2 = 169 -QD^2
QD =(169 + 225 -196) / 30 = 66 / 10 =33 / 5 = 6,6 cm
Ondorioz, PQ = PD – QD = 9,6 – 6,6 = 3 cm
Beti bezala, problema interesgarriak jartzen dizkigu Javierrek. Eskerrik asko!
Ondo izan!