Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta aurten ere, udako oporretan egiteko asteazkenero ariketa matematiko bat izango duzue, Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.
Hona hemen gure bigarren ariketa: Pizza jaten.
Zenbat modutan har daitezke pizzaren zortzi zatietatik hiru, elkarren alboko bi hartu barik? Utzi zuen erantzuna iruzkinetan!
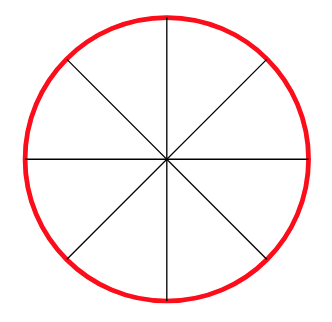
Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain, tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.
Ariketak “Calendrier Mathématique 2022. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.
2 iruzkinak
Problema polita, neuronak dantzan jartzera gonbidatzen duen horietakoa.
Ziur aski, zenbaketa egiteko modu desberdinak daude. Nik honako hau erabili dut:
Pizzaren zatiak zenbakitu (1-2-3-4-5-6-7-8) eta zati bakoitza oktogono baten erpinekin identifikatzen badira, jatorrizko problema hurrengo problema baliokidean bihurtzen da: ondoz ondokoak ez diren oktogono baten hiru erpin elkartuz, zenbat triangelu desberdin eraiki daitezke?
Hasteko, 1. erpina aukeratu eta finkatu egingo dugu. Erpin honekin 6 triangelu desberdin marraz ditzakegu: 135, 136, 137, 146, 147 eta 157. Era berean, 2.a finkatuta, beste 6 triangelu: 246, 247, 248, 257, 258 eta 268. 3.arekin sei ere: 357, 358, 351 (hau errepikatuta, 135 triangelua da), 368, 361 (136 triangeluaren berdina) eta 371 (=137)… Horrela jarraituta, erpin bakoitza finkatuz, 6 triangelu eratu ditzakegu. Denera: 8 erpin bider 6 triangelu = 48 triangelu. Baina, ikusten denez, batzuk errepikatuta daude, adibidez: 135 (1 finkatzean), 351 (3 finkatuta) eta 513 (5 finkatzean). Hau da, triangelu bakoitza hiru aldiz kontatu dugu.
Beraz, denera 48/3 = 16 triangelu desberdin; ondorioz, 16 modu daude pizzaren zatiak aukeratzeko elkarren ondoko bi hartu gabe.
Problema hau orokortu daiteke n zati edo erpinetarako (n = 6 edo handiagoa izanik). Oker ez banabil, zati kopurua honakoa da n-ren menpe: Z = 1/6·(n-5)·(n-4)·n
Azken adierazpenaren azalpen bat:
n erpin; Z= n·(triangelu kopurua)·(herena)
n=6; Z=6·(1)·1/3=6·(1·2·1/2)·1/3=6·(6-5)(6-4)·1/6
n=7; Z=7·(3)·1/3=7·(2·3·1/2)·1/3=7·(7-5)(7-4)·1/6
n=8; Z=8·(6)·1/3=8·(3·4·1/2)·1/3=8·(8-5)(8-4)·1/6
n=9; Z=9·(10)·1/3=8·(4·5·1/2)·1/3=9·(9-5)(9-4)·1/6
……….
n=k; Z = k·(k-5)(k-4)·1/6
[…] 2. Zenbat modutan har daitezke pizzaren zortzi zatietatik hiru, elkarren alboko bi hartu barik? […]