Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta aurten ere, udako oporretan egiteko astelehenero ariketa matematiko bat izango duzu, Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.
Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain, tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.
Hona hemen gure azken ariketa: Luzeren bila.
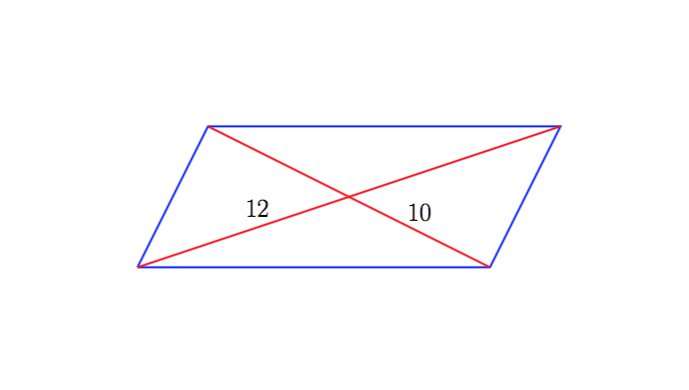
6) Paralelogramo baten azalera 36 cm2 da eta diagonalen neurriak 12 cm eta 10 cm dira. Aurkitu aldeen luzerak.
Ariketak “Calendrier Mathématique 2019. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.
3 iruzkinak
Beno, Interneten kuxkuxeatu dut paralelogramoen formulak aurkitzeko, zeren ez nuen honetaz ezer oroitzen. Ulertzen dudanagatik diagonalak edukita, hauen mozketa angelua beharrezkoa da aldeen luzera lortzeko, triangelu bat baita. Eta, dirudienez, mozketa angelu hori azalera eta diagonalak erabilita kalkula daitezke.
Azalera = (e diagonala • f diagonala • sin mozketa)/2
36 = (10 • 12 • sin mozketa) / 2
arcsin ((2 • 36) / (10 • 12)) = mozketa
mozketa angelua = 36,8699º
Mozketa angulo hori erabilita
2a^2 = e diagonala^2 + f diagonala^2 – 2 e f cos mozketa angelua
2b^2 = e diagonala^2 + f diagonala^2 + 2 e f cos mozketa angelua
2a^2 = 10^2 + 12^2 – 2•10•12 cos 36,8699º
2b^2 = 10^2 + 12^2 + 2•10•12 cos 36,8699º
a aldea = 6,0827
b aldea = 9,2195
eta beste bi aldeak hauen berdinak direnez, ba horiek dira aldeen luzeerak
Ez dakit azken ariketa hau ez ote zaidan espero baino korapilatsuago suertatu. Niri azkenean bigarren graduko ekuazio bat atera zait, non bere bi soluzioak posible izan diren. Haeku dira nire emaitzak;
a=4.8132 b=8.7654
a=8.7654 b=4.8132
Pixka bat laburbilduz nire arrazonamentua honako hau izan da; diagonalak eta Pitagoras kontuan hartuz;
a) 12^2=144=[a+dcos(B)]^2+[dsen(B)]^2
b) 10^2=100=[a-dcos(B)]^2+[dsen(B)]^2
1) Berez 144-100=44={[a+dcos(B)]^2+[dsen(B)]^2}-{[a-dcos(B)]^2+[dsen(B)]^2}
bestalde area jakiña da a x h=36 non h=dsen(B)
Honekin atera dezakegu 1) simplifikatuz ateratzen zaigu a=42,19004/d
Eta beste alde batetik B=arctg(1.6363)=58.5704
Nondik atera dezakegu dcos(B) eta dsen(B) baloreak.
a) ekuazioan balore ezagunak ordezkatuz aipatutako bigarren graduko ekuazioa ateratzen zait emandako bi emaitzekin.
Bihurri xamarra, seguru hanka sartu dudala nonbait. Hala bada hanka sartzeak ere ikasteko aukera bikaina.
Buelta batzuk eman dizkiot problemari eta ebazteko hiru forma planteatu ditut: triangulu baten azalera aldeen menpe ematen digun Heron Alexandriakoaren formula bikainaren bidez, triangelu zuzenak erabiliz (aukera desberdinak daude aukeratutako triangeluen arabera) eta kosinuaren teorema erabiliz. Ondorengo loturan hiru ebazpenen zirriborroa ikusgai:
https://drive.google.com/file/d/1BbqYT7b0Yw0XN4f_8drx2v-beB70n9q_/view?usp=sharing
Ea zuzen bideratuta dauden ebazpenak. Gustura aritu naiz, eta, duda barik, problemak ebaztea osasungarria da.