Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta aurten ere, udako oporretan egiteko astelehenero ariketa matematiko bat izango duzu, Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.
Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain, tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.
Hona hemen gure hirugarren ariketa: Triangeluaren azalera.
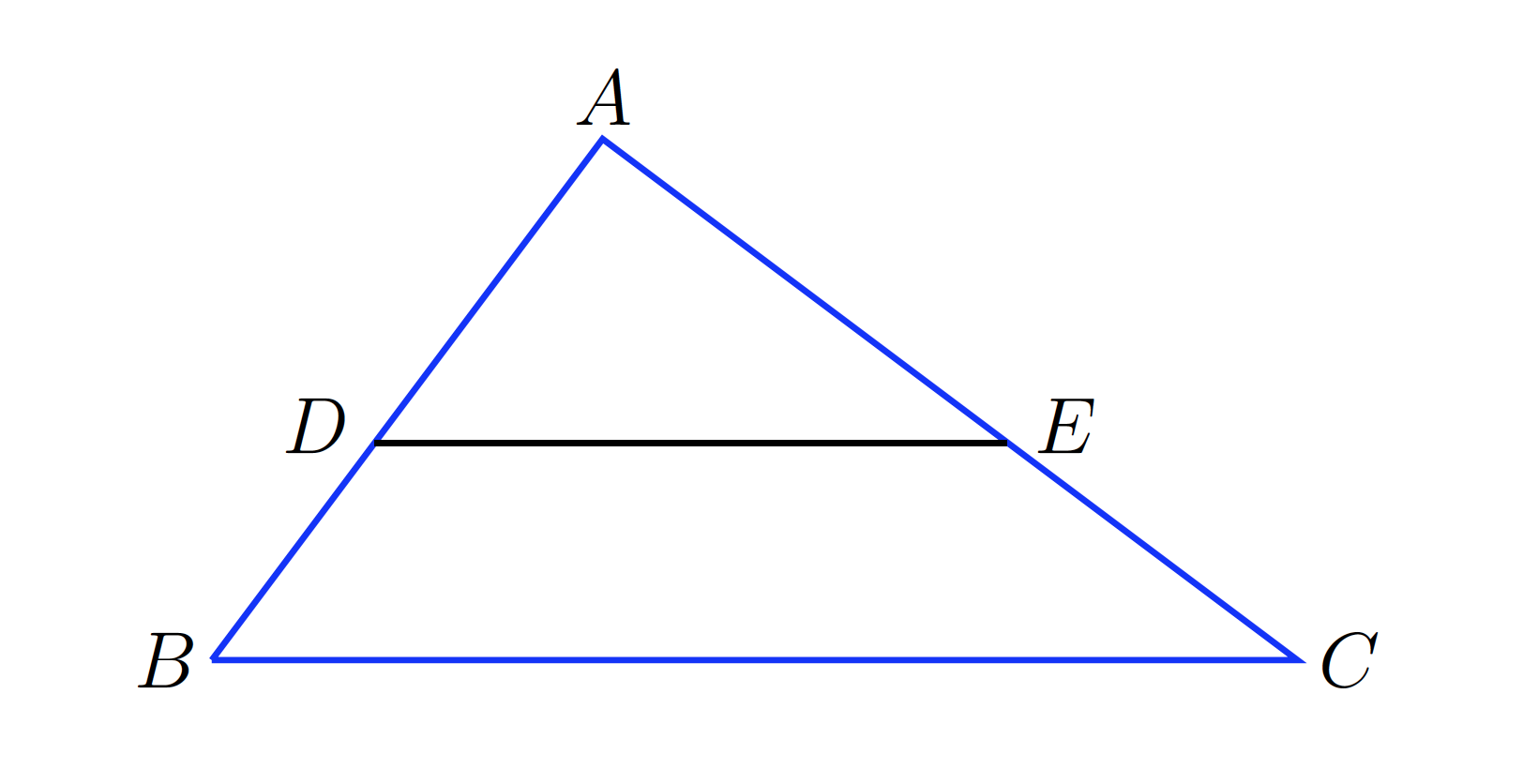
3) ABC triangelua zuzena da (A-n du angelu zuzena). AB= 3 m eta AC = 4 m dira. DE eta BC paraleloak dira eta 1 m da bien arteko distantzia. Zein da ADE triangeluaren azalera?
Ariketak “Calendrier Mathématique 2020. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.
3 iruzkinak
Niri 2.041666 ateratzen zait.
Zaila zait azalpenak emantera argazkirik ipini gabe, saiatuko naiz.
Dakiguna zerako hau da, hirukia zuzena dela (aterako ditugun hiruki guztiak zuzenak eta baliokideak izango dira, hauxe da, neurri ezberdinak izan arren angelu berdiñak izango dituzte).
B erpinean ikuska dezakegu hiruki hoietako bat non kateto bat 1 balio du (datu hau emana dator), beste katetoa b izenda dezakegu eta hipotenusa a. Hirukiak baterakide direnez gero;
4/3=1//b, b=3/4, Pitagoras aplikatuz atera dezakegu a=5/4=1.25. ADE hirukiaren AD katetoa 3-1.25=1.75.
Hirukiak bateragarriak direnez gero;
C/A=4/3=c/1.75, c=2.3333, non c den hirukiaren altura edo garaira. Area kalkulatzeko;
A(t)=bc/2=1.75*2.3333/2=2.041666m^2. Niri horrela atera zait.
Kaixo!
Ba bide ezberdinak erabiltzen saiatu naiz, baina beti kale itsu batera heltzen naiz, asike Irailean ezagutuko dut bide zuzena 😂😂😂
Asko eta ondo zaindu,
K
[…] ABC triangelua zuzena da (A-n du angelu zuzena). AB = 3 m eta AC = 4 m dira. DE eta BC paraleloak dira […]