Tentsoreak matematiketan eta zientzian erabiltzen dira ezkutuko egi geometrikoak ezagutzera emateko. Baina, zer dira?
Albert Einsteinek bere erlatibitatearen teoria berezia 1905ean argitaratu ondoren, hurrengo hamarkada osoa eman zuen grabitatearen teoria garatzen. Hala ere, urteak eman zituen etengabeko arazo bati aurka egiten.
Erakutsi nahi zuen grabitatea espazio-denboraren geometriaren deformazioa dela, materiaren presentziaren ondoriozkoa. Hala ere, intuizioak kontrakoa esaten badigu ere, bazekien denbora eta distantzia erlatiboak direla: erreferentzia-esparruaren arabera aldatu egiten dira. Azkar mugitzeak distantzia murriztu eta denbora geldotzen du. Hortaz, nola deskribatu daiteke grabitatea objektiboki, geldirik gauden edo mugitzen ari garen alde batera utzita?

Einsteinek galdera horren erantzuna teoria geometriko berri batean aurkitu zuen; Gregorio Ricci-Curbastro eta Tullio Levi-Civita matematikari italiarrek argitaratu zuten urte batzuk lehenago. Teoria horretan, geroago “tentsore” izenez ezagutuko zen terminoaren oinarri matematikoak ezarri zituzten.
Geroztik, tentsoreen zeregina oinarrizkoa izan da Einsteinen erlatibitatearen teorian ez ezik, ikaskuntza automatikoan, mekanika kuantikoan zein biologian. «Gure ekuazioak antolatzeko paketatze-mekanismo efizienteena dira tentsoreak», azaldu du Dionysios Anninos-ek, Londresko King’s College-eko fisikari teorikoak. «Objektu geometrikoen lengoaia naturala dira».
Halaber, definitzen zailak dira. Informatikari bati galdetuz gero, tentsore bat datu garrantzitsuak biltzen dituen zenbakien matrize bat izan daiteke. Zenbaki bakar bat “0 mailako” tentsore bat da. Zenbakien zerrenda bat, bektore deritzona, 1. mailako tentsorea da. Zenbakien sareta bat, matrize deritzona, 2. mailako tentsorea da; eta horrela hurrenez hurren.
Baina fisikari edo matematikari bati galdetzekotan, definizio hori ez dute nahikotzat joko. Tentsoreak zenbakien antolamendu horren bidez irudikatu daitezkeen arren, esanahi geometriko sakonagoa dute.
Tentsoreen zentzu geometrikoa ulertzeko, bektoreetara jo behar dugu. Imajina ezazu bektorea espazioan flotatzen duen gezi bat dela: luzera eta norabidea dauzka. (Gezi horrek ez du puntu espezifiko batean ainguratuta egon behar: espazioan mugituz gero, bektore bera izaten jarraituko du). Bektore batek, adibidez, partikula baten abiadura irudika dezake: luzerak azkartasuna adierazten du, eta norabideak, berriz, ibilbidea.
Informazio hori zenbakien zerrenda batean paketatzen da. Bi dimentsioko espazio batean dagoen bektore bat, adibidez, bi zenbakiren bitartez definitzen da. Lehenengoak gezia eskuinerantz edo ezkerrerantz zenbat unitate hedatzen den adierazten du, eta bigarrenak, berriz, gora edo behera zenbat hedatzen den.
Hala ere, zenbaki horiek koordenatuen sistemaren definizioaren araberakoak dira. Demagun zure koordenatuen sistema aldatzen duzula:
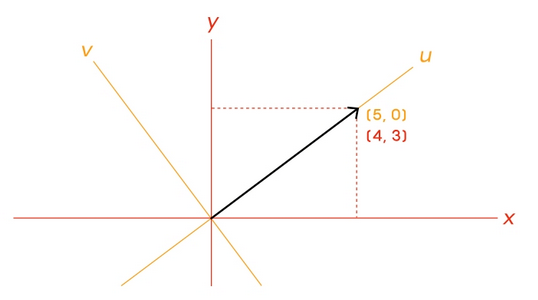
Orain bektorea koordenatuen sistema berriaren norabide bakoitzean duen hedaduraren arabera adierazten duzu, eta, horren ondorioz, emaitza bestelakoa da. Hala ere, bektorea ez da aldatu: luzerak eta norabideak berdin jarraitzen dute, zure koordenatuen sistema edozein dela ere. Gainera, koordenatuen sistema batetik bestera nola aldatu baldin badakizu, automatikoki jakingo duzu nola aldatu beharko litzatekeen zure zenbakien zerrenda.
Tentsoreek ideia horiek orokortzen dituzte. Bektore bat 1. mailako tentsorea da; goragoko maila duen tentsoreek informazio geometriko konplexuagoa dute.
Demagun, adibidez, altzairuzko bloke bat duzula, eta haren gainean egin daitezkeen indar guztiak deskribatu nahi dituzula. 2. mailako tentsore baten bidez lor dezakezu, matrize gisa idatzita. Blokearen alde bakoitzak hiru norabide desberdinetatik jasotzen ditu indarrak. (Adibidez, blokearen eskuineko aldeak behetik gorako, ezkerretik eskuinerako eta atzetik aurrerako indarrak jasan ditzake).
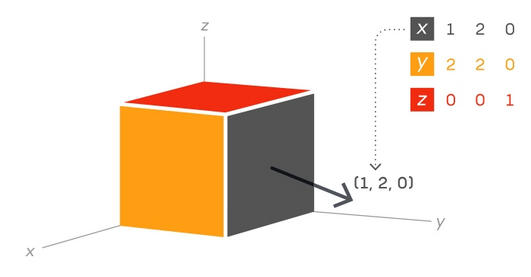
Hortaz, indar horiek guztiak barne hartzen dituen tentsorea irudikatzeko 9 zenbakiko matrize bat erabil daiteke; hau da, zenbaki bana alde bakoitzean jasotzen duen indar bakoitzeko. (Kasu honetan kontrako aldeak erredundanteak dira).
Matematikariek tentsoreak bektore bat edo gehiago hartu eta beste bektore bat edo zenbaki bat sortzen duten funtzio gisa ulertzen dituzte. Hala ere, sortzen duten zenbaki hori ez da hautatutako koordenatuen sistemaren araberakoa. (Murrizketa horrek bereizten ditu tentsoreak funtzio orokorretatik). Tentsore batek, adibidez, laukizuzen baten ertzak osatzen dituzten bi bektore hartuko balitu, laukizuzenaren azalera sor lezake. Laukizuzena biratuko bagenu, x ardatzarekiko luzera eta y ardatzarekiko altuera aldatuko lirateke, azalera aldatu gabe.
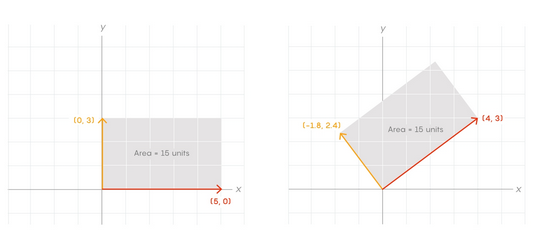
Einsteinen erlatibitatearen teorian, distantzia eta denbora aldakorrak dira behatzaile desberdinentzat, aurretik absolututzat jotzen baziren ere. Hala ere, luzera eta altuera azalera kalkulatzeko konbinatu daitezkeen bezala, distantzia eta denbora ere konbinatu daitezke, bestelako propietate finkoak edo inbarianteak definitzeko. Tentsoreei esker, Einsteinek eraginkortasunez manipulatu zituen inbariante horiek, masa eta espazio-denboraren arteko erlazioa deskribatzeko. Ekuazio bakar baten bidez deskribatu zuen espazio-denboran materia kurboa nolakoa zen; hau da, kondentsatu zuen 16 ekuazio independente eta interkonektatuen bidez kalkulatu beharreko prozesua.
Ekuazio hori 1915ean argitaratu zenetik, tentsoreak nonahiko bihurtu dira. Fisikariek elektroiek nukleo atomikoen inguruan egindako mugimendua karakterizatzeko edo lotutako sistema kuantiko baten egoera deskribatzeko erabiltzen dituzte; informatikariek ikaskuntza automatikoko ereduen parametroak biltegiratzeko erabiltzen dituzte; biologoek leinuan zehar bereizgarriak arakatzeko erabiltzen dituzte; eta matematikariek, berriz, tentsore konplexuagoak lortzeko biderkatu eta horien espazio berriak aztertzen dituzte. Tentsoreei esker, matematikariek besteak beste simetria konplexuak miatu, forma berezien ezaugarriak (aldagai izenez ezagunak) aztertu eta funtzio desberdinen arteko harremanak iker ditzakete.
Einsteinek behin lagun bati eskatu zion tentsoreak ulertzen lagun zezala, erotuko zelakoan. Alabaina, ulertu egin zituen, eta geroztik ezinbestekoak izan dira zientzialariek gure mundua deskribatu ahal izateko.
Jatorrizko artikulua:
Joseph Howlett. (2025). The Geometric Tool That Solved Einstein’s Relativity Problem, Quanta Magazine, 2024ko abuztuaren 12a. Quanta Magazine aldizkariaren baimenarekin berrinprimatua.