Alan Turing eta pentsamendu negatiboaren boterea
Diagonalizazioa izeneko teknika batean oinarritutako proba matematikoak erabat aurkakoak izan daitezke, baina algoritmoen mugen berri ematen laguntzen dute.
Algoritmoak toki guztietan daude. Gure bidaiak optimizatzen dituzte, ordainketak prozesatzen dituzte eta trafikoaren fluxua koordinatzen dute Interneten. Termino matematiko zehatzetan artikulatu daitekeen arazo bakoitzarentzat hori ebatz dezakeen algoritmo bat dagoela dirudi, gutxienez printzipioz.

Baina ez da hala: itxuraz arruntak diren zenbait problema inoiz ere ezin dira algoritmoen bidez ebatzi. Alan Turing zientzialari informatiko aitzindariak duela ia mende bat erakutsi zuen arazo “konputaezin” horiek bazirela, informatika modernoaren abiapuntu izan zen konputazioaren modelo matematikoa formulatu zuen artikulu berdinean.
Turingek emaitza berritzaile hori erakusteko intuizioaren aurkako estrategia bat erabili zuen: ebazteko saio oro arbuiatzen duen problema bat definitu zuen.
«Zer egiten ari zaren galdetzen dizut eta gero esaten dut: ‘Ez, beste zerbait egitera noa’», azaldu du Rahul Ilangok, Massachusettseko Teknologia Institutuko graduondoko ikasle batek, informatika teorikoa ikasten ari dena.
Turingen estrategia diagonalizazioa izeneko teknika matematiko batean oinarritzen da eta historia entzutetsua du. Hona hemen proba horren logikaren azalpen sinplifikatua.
Kateen teoria
Diagonalizazioa bit katea baten problema arrunt bat ebazteko trikimailu argi baten ondorioz sortu zen. Bit bakoitza 0 edo 1 izan daiteke, eta kate horien zerrenda bat emanda, denak luzera berekoak, sortu daiteke zerrendan ez dagoen kate berri bat?
Estrategiarik errazena da balizko kate bakoitza txandaka hartzea kontuan. Demagun bost kate dituzula, bakoitza bost biteko luzerakoa. Hasi zerrenda errepasatzen 00000 aurkitzeko. Ez badago, geratu; baldin badago, pasa 00001era eta errepikatu prozesua. Nahiko sinplea da, baina mantsoa, kate luzeen zerrenda luzeetarako.
Diagonalizazioa ikuspegi alternatiboa da eta pixkanaka eraikitzen du kate berri bat. Hasi zerrendako lehenengo kateko lehenengo bitarekin eta inbertitu; hori izango da zure kate berriko lehenengo bita. Gero inbertitu bigarren kateko bigarren bita eta kate berriko bigarren bita izateko erabili eta errepikatu zerrendaren amaierara iritsi arte. Inbertitzen dituzun bitek bermatu egiten dute kate berria eta jatorrizko zerrendako kate bakoitza desberdinak izango direla gutxienez toki batean. (Kate zerrendaren bidez lerro diagonal bat ere eratzen da eta horrek ematen dio izena teknikari).
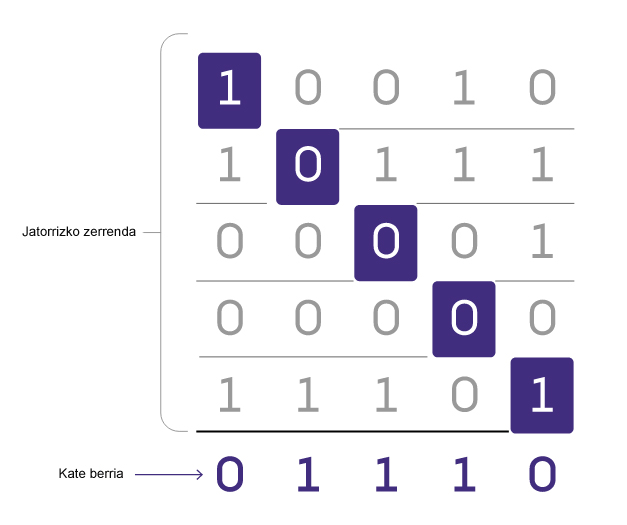
Diagonalizazioak zerrendako kate bakoitzeko bit bakarra aztertu behar du, beraz, beste metodoak baino askoz azkarragoa izaten da. Baina infinituarekin duen jokabide ona da diagonalizazioaren egiazko boterea.
“Orain kateak infinituak izan daitezke; zerrenda infinitua izan daiteke; eta hala ere funtzionatu egiten du”, dio Ryan Williams MITeko zientzialari informatiko teorikoak.
Ahal hori aprobetxatu zuen lehenengo pertsona Georg Cantor izan zen, multzoen teoriaren azpiatal matematikoaren sortzailea. 1873an Cantorrek diagonalizazioa erabili zuen infinitu batzuk besteak baino handiagoak zirela erakusteko. Handik sei hamarkadara, Cantorren diagonalizazioaren bertsioa konputazioaren teoriara egokitu zuen Turingek, kontrakorrentean zen tonu argia emanaz.
Mugapenaren jolasa [*]
Turingek erakutsi nahi zuen bazirela inongo algoritmok ebatzi ezin zituen problema matematikoak, hau da, sarrerak eta irteerak ongi definitutako problemak baina sarreratik irteerara joateko prozedura hutsezinik gabeak. Egiteko lauso hori erabilerrazago bihurtu zuen erabakitzeko problemak soilik hartu zituenean, non sarrera zeroen eta batekoen edozein kate izan daitekeen eta irteera 0 edo 1 den.
Zenbaki bat zenbaki lehena (1ekin eta bere buruarekin bakarrik zatitu daitekeena) den zehaztea da erabakitzeko problema baten adibidea: zenbaki bat ordezkatzen duen sarrerako kate bat emanda, irteera zuzena 1 da zenbaki lehena bada eta ez bada, 0 da irteera zuzena. Beste adibide bat da programa informatikoak egiaztatzea, sintaxiko akatsen bila (akats gramatikalen parekidea). Hemen sarrerako kateek kode bat irudikatzen dute programa desberdinetarako (programa guztiak horrela irudikatu daitezke, horrela biltegiratzen eta exekutatzen baitira ordenagailuetan) eta xedea da 1 sortzea kodeak sintaxiko akatsen bat badu eta 0 sortzea, akatsik ez badu.
Algoritmoak problema ebatziko du, soilik irteera zuzena sortzen badu balizko sarrera bakoitzerako; huts egiten badu, behin bakarrik egin arren, ez da algoritmo generalista izango problema horrentzat. Eskuarki, lehenengo ebatzi nahi dizun problema zehaztuko zenuke eta gero hori ebazteko algoritmo bat aurkitzen saiatuko zinateke. Turing ebatzi ezin ziren problemen bila zebilen eta logika horri bira eman zion: algoritmo posible guztien zerrenda infinitua irudikatu zuen eta diagonalizazioa erabili zuen, zerrendako algoritmo guztiek porrot egiteko moduko problema etengabe bat eraikitzeko.
Demagun ’20 galderako’ [**] prestatutako joko bat, non buruan objektu jakin bat dugula hasi ordez, erantzuten duenak (‘erantzuleak’) aitzakia bat asmatzen duen galdera bakoitzari ez esateko. Jokoaren amaieran, falta zaizkion kualitateen bidez erabat definitutako objektu bat deskribatu da.
Turingen diagonalizazioaren proba, joko horren bertsio bat da non galderek algoritmo posibleen zerrenda infinitua igarotzen duten, behin eta berriro galdetuz: «Algoritmo horrek ebatzi al dezake inkonputagarria dela erakutsi nahiko genukeen problema?»
«’Galdera infinituak’ moduko bat da», esan du Williamsek.
Jokoa irabazteko, Turingek problema bat landu behar zuen algoritmo bakoitzaren erantzuna ez izango zena. Horrek esan nahi du sarrera partikular bat identifikatzea lehenengo algoritmoak erantzun okerra sortzeko, beste sarrera batek bigarrenaren okerra sortzea eta horrela, denekin. Sarrera berezi horiek aurkitu zituen Kurt Gödel-ek duela gutxi erabili zuen antzeko trikimailu bat erabilita; Gödelek horrelakoak erabili zituen erakusteko “baieztapen hau ezin da demostratu” bezalako baieztapen autoerreferentzialak problemak direla matematikaren funtsentzat.
Ideia giltzarria izan zen algoritmo (edo programa) bakoitza zero eta bat zifren katea bezala irudikatu daitekeela. Horrek esan nahi du, akatsak egiaztatzeko programaren adibidean bezala, algoritmo batek beste algoritmo baten kodea har dezakeela sarrera gisa. Printzipioz, algoritmo batek bere kodea ere har dezake sarrera gisa.
Ideia horrekin, Turingen probakoa bezalako problema ez konputagarri bat defini dezakegu: “Algoritmo baten kodea irudikatzen duen sarrerako kate bat emanda, 1 sortzen du algoritmo horrek 0 sortzen badu bere kodea sarrera denean; aitzitik, irteera 0 da”. Problema hau ebazten saiatzen den algoritmo bakoitzak irteera okerra emango luke gutxienez sarrera batean, hau da, bere kodeari dagokion sarreran. Horrek esan nahi du problema zital hori ezin dela ebatzi inongo algoritmoren bidez.
Negazioak egin ezin duena
Informatikariek oraindik ez dute diagonalizazioarekin amaitu. 1965ean Juris Hartmanis eta Richard Stearns-ek Turingen argumentua egokitu zuten erakusteko problema konputagarri guztiak ez direla berdinak: batzuk berez besteak baino zailagoak dira. Emaitza horrek hasi zuen konplexutasun konputazionalaren teoriaren alorra, problema konputazionalen zailtasuna aztertzen duena.
Baina konplexutasunaren teoriak Turingen aurkako metodoaren mugak ere erakutsi zituen. 1975ean, Theodore Baker, John Gill eta Robert Solovay-k erakutsi zuten konplexutasunaren teorian irekitako gai asko inoiz ezin direla ebatzi soilik diagonalizazioa erabilita. Horietan nagusia P eta NP konplexutasun moten problema ospetsua da, non galdetzen den erraz egiazta daitezkeen irtenbideak dituzten problema guztiak algoritmo egokiarekin ebazteko ere errazak al diren.
Diagonalizazioaren puntu itsuak abstrakzio maila altuaren zuzeneko ondorioak dira eta abstrakzio maila horrek egiten du diagnolazizaioa hain ahaltsu. Turingen demostrazioak ez zuen praktikan sor zitekeen problema konputaezinek aipatzen; aldiz, mota horretako problema bat asmatu zuen sortu ahala. Diagonalizazioaren beste proba batzuk ere oso aldenduta daude mundu errealetik, beraz, ezin dituzten ebatzi mundu errealeko xehetasunek garrantzia duten gaiak.
«Urruneko konputazioa darabilte» dio Williamsek. «Tipo bat irudikatzen dut birus baten aurrean eta birus horrengana eskularru-kaxa baten bidez heltzen».
Diagonalizazioaren porrota adierazle goiztiarra izan zen, P eta NP kategoriako problemak ebaztea bide luzea izango zela argi uzten zuena. Mugak izan arren, diagonalizazioa tresna giltzarria da konplexutasunaren teorikoen pilan. 2011n Williamsek beste teknika batzuekin batera erabili zuen konputazio eredu murriztu jakin batek ezin zituela ebatzi problema bereziki zail batzuk, ikertzaileek 25 urtez emaitza horri heldu ez zioten arren. P eta NP kategorien problema ebaztetik oso urrun zegoen, baina aurrerapen handia izan zen.
Zerbait ez dela posible erakutsi nahi baduzu, ez gutxietsi ez esate soilaren boterea.
Itzultzailearen oharrak:
[*] Ingeleseko jatorrizkoa, “The limitation game”, hitz-joko bat da “The Imitation Game” filmaren izenburuan oinarritua; film hori Alan Turingen bizitza eta obrako alderdi batzuei buruzkoa da.
[**] ‘20 galdera’ izeneko jokoan erantzuten duenak (‘erantzuleak’) gainerako jokalariek (interrogatuek) igarri beharreko zerbait aukeratzen du. Galderak egiten dituzte txandaka eta erantzuleak «bai» edo «ez» erantzun behar du. Hona hemen galderen adibide batzuk: «Mugikor bat baino handiagoa da?», «Bizirik dago?» eta, amaitzeko, «Boligrafo hau da?». Ezin da gezurrik esan. Interrogatzaile batek erantzun zuzena asmatzen badu, irabazi egiten du eta hurrengo txandako erantzulea izango da. 20 galdera egin eta erantzun zuzenik ez bada, erantzuleak irabazten du eta hurrengo txandan ere bera izango da erantzulea.
Jatorrizko artikulua:
Ben Brubaker (2023). Alan Turing and the Power of Negative Thinking, Quanta Magazine, 2023ko irailaren 5a. Quanta Magazine aldizkariaren baimenarekin berrinprimatua.