Alan Turing, morfogenesiaren oinarriak matematikarekin azaltzen

Jone Apraiz Iza, Idoia Marauri Bernedo

1952 urtean, The Chemical Basis of Morphogenesis artikuluaren argitalpenarekin, Alan Mathison Turing matematikariak biologia matematikoaren arloa aztoratu egin zuen ideia iraultzaileak berera ekarriz. Ordutik, ideia horiek zientziako arlo ezberdinak elikatu izan dituzte, adibidez, matematika, fisika eta adimen artifiziala.

Morfogenesia enbriologiaren arlo bat da. Morfogenesi hitzaren itzulpen literala “formaren jatorria” da. Berez, morfogenesia organismo batek etorkizunean izango duen eta enbrioian ematen den formaren sorrera- eta garapen-prozesuari deritzo.

The Chemical Basis of Morphogenesis artikuluan morfogenesiaren inguruko edukiak ulertzeak Turingen ikerketek bere garaian eta aurrerantzean izan duten garrantziaz jabetzera lagun diezaguke. Bestetik, biologia matematikoaren ondorengo ikerketa-bideak nondik jarraitu izan duten hobeto ezagutzeko aukera ematen digu. Horregatik, laburpen honekin eta ikerlanarekin, irakurlea Turingen artikuluan agertzen diren matematikako tresnak eta ideiak zehaztasun eta sakontasun gehiagorekin ulertzera gonbidatzen dugu.

Matematika morfogenesia azaltzeko

Turingek, bere artikuluan, biologiarekin zein kimikarekin erlazionatuta dagoen morfogenesiaren mekanismoa ikertu zuen, landareetan zein animalien ilajeetan agertzen diren patroiak aztertu nahian. Horretarako, matematikako kontzeptu eta baliabide ezberdinak erabili zituen: ekuazio diferentzialak, deribatu partzialetako ekuazioak, erreakzio-difusio ekuazioak, Fourierren serieak eta funtzioen linealizazioa, besteak beste.

Artikuluan, ehunez osatutako masetan dauden morfogeneen (aztertu zituen substantzia kimiko arbitrarioei eman zien izena) jarrera ezagutzeko, egoera eta eremu sinpleenak aztertzen hasi zen Turing. Bi eredu matematiko hauek aurkeztu zituen: eraztun diskretuko eta eraztun jarraituko eremuak, artikuluko Reactions and Diusion in a Ring of Cells eta Continuous Ring of Tissue ataletan, hurrenez hurren.

Eraztun diskretuko eremuan, erreakzio-difusio ekuazioen ondorengo sistema planteatu zuen Xr = X(r, t) eta Yr = Y (r, t) morfogeneen kontzentrazioen aldaketa azaltzen saiatzeko:

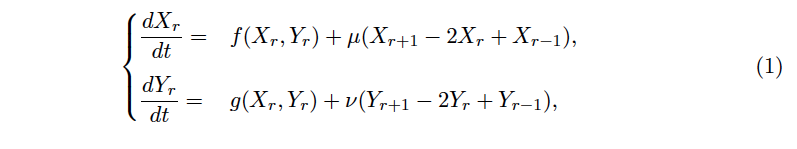
∀ r ∈ (1,…, N), izan ere, eraztun diskretuan N zelula daudela suposatu zuen. Hau da, eraztuneko zelula bakoitzarentzako horrelako sistema bat betetzea eskatu zuen.

Deskribatzen ari garen (1) sisteman, ekuazio bakoitzeko eskuinaldeko bigarren batugaiek morfogeneek jarraitzen duten difusio-prozesua adierazten dute, μ eta ν parametroak zelularteko difusio-koezienteak izanik. Bestalde, f eta g funtzioek (erreakzio-zinetiko gisa ezagutzen direnak) Xr eta Yr morfogeneen substantzien kontzentrazio-aldakuntzak definitzen dituzte, erreakzio-prozesuaren adierazpide dira.

(1) sistemaren soluzioa bilatzeko, lehenik eta behin, Turingek sistema linealizatu zuen Taylorren garapenak erabiliz. Hau da, f eta g funtzio linealen bidez hurbildu zituen oreka-puntu baten inguruan. Ondoren, jatorrizko kontzentrazioen gorabeherak adierazten dituzten xr zein yr funtzioen Fourierren seriezko garapenak lortuta eta sisteman ordezkatuta, Kalkuluko deribatuen eta serieen emaitza teorikoetan oinarrituta, (1) sistema ebazteko gai izan zen.

Eraztun jarraituko eremurako, deribatu partzialetako ekuazioez baliatuta, erreakzio-difusio ekuazioetako sistema hau planteatu zuen Turingek:

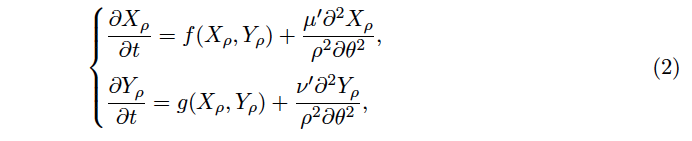
non Xρ = X (ρ, θ , t) eta Yρ = Y (ρ, θ , t) funtzioek t uneko, θ ∈ [0, 2π] angeluko (OX ardatzarekiko neurtuta) eta ρ erradio finkoko eraztuneko puntuko substantzia kimikoen kontzentrazioak adierazten dituzten. Bestalde, ρ ∈ (ρ1, ρ2) dago (ρ1 eta ρ2 aztertzen ari garen eraztunaren bi erradioak dira) eta f(Xρ, Yρ) zein g(Xρ, Yρ) morfogeneen arteko erreakzioaren adierazpide dira. Bigarren ordenako terminoak difusioaren adierazle dira, µ’ eta ν’ zelulen arteko difusio-koezienteak izanik. (2) sistemaren soluzioa bilatzeko, eraztun diskreturako erabilitako baliabide matematikoen antzekoak aplikatu zituen Turingek.

Aurretik txertatu ditugun eredu matematikoak planteatuta, Turingek forma biologikoak substantzia kimikoen kontzentrazioetako aurrereduei jarraiki sortzen zirela iradoki zuen. Hau izan zen bere proposamena: morfogeneak era “egokian” erreakzionatuz eta hedatuz gero, morfogeneen kontzentrazioetan espazio-patroiak era zitezkeela baldin eta hasierako zelulen bilduraren banaketa uniformea bazen. Hau da, hasierako substantzia kimikoen sistema “nahiko” homogeneoa izango balitz, denbora pasa ahala, ausazko desorekek oreka-puntu homogeneoetan eragiten zituzten ezegonkortasunengatik, patroi bat baino gehiago garatuko liratekeela, Turingen patroi deritzenak.

Artikuluaren fitxa:

• Aldizkaria: Ekaia
• Zenbakia: Ekaia 41
• Artikuluaren izena: Alan Turing-ek morfogenesiaren inguruan
  egindako ikerketaren analisi matematikoa.
• Laburpena: Artikulu honetan, Alan Turing matematikariak 1952an morfogenesiaren inguruan aurkeztu zuen The Chemical Basis of Morphogenesis lanaren zati bat aurkeztu eta matematikoki garatu da. Horretarako, beharrezkoak diren matematikako kontzeptuak eta baliabideak azalduko dira. Konkretuki, Alan Turingek artikuluko «Reactions and Diffusion in a Ring of Cells» (eraztun diskretuko eremua) eta «Continuous Ring of Tissue» (eraztun jarraituko eremua) ataletan gehiegi sakondu edo zehaztu gabe erabili zituen ekuazio diferentzialak, erreakzio-difusio ekuazioak, Fourierren serieak eta funtzioen linealizazioa azaltzen dira, eta bi eremu horietan planteatutako ekuazio-sistemen soluzioak bilatzeko erabili dituzte egileek. Artikulua UPV/EHUko Idoia Marauri ikasle ohiaren Gradu Amaierako Lanean oinarrituta dago.
• Egileak: Jone Apraiz Iza, Idoia Marauri Bernedo
• Argitaletxea: UPV/EHUko argitalpen zerbitzua
• ISSN: 0214-9001
• eISSN: 2444-3255
• Orrialdeak: 275-310
• DOI: doi.org/10.1387/ekaia.22214

Egileez:

Jone Apraiz Iza eta Idoia Marauri Bernedo UPV/EHUko Zientzia eta Teknologia Fakultateko Matematika Saileko ikertzaileak dira.

Ekaia aldizkariarekin lankidetzan egindako atala.