Hatz-markak, FBI eta Fourier modernizatua

Javier Duoandikoetxea

Hatz-markek identifikatu egiten gaituzte. Horregatik, hatz-marken bila ibiltzen dira detektibeak delitu bat gertatu den lekuan. Ez da inor harrituko, bada, esaten badugu hatz-marken bilduma erraldoiak daudela polizien artxiboetan.

FBI 1924an hasi zen hatz-markak hartzen. Tintan bustita uzten zuten atzamarrek marka kartoizko fitxetan. FBIk 25 milioi fitxatik gora zituen gordeta 1993an. Ordurako, ordenagailuen erabilera hedatzen hasia zen eta argi zegoen artxibo digitalak izatea onura handikoa izango zela, bai hatz-markak gordetzeko, bai bilaketak egiteko. Hortaz, digitalizazioari ekin zioten.

Garrantzitsua da ahalik eta zehaztasun handienaz ziurtatzea norena den hatz-marka bat. Horregatik, digitalizazioa egiteko hazbete bakoitzeko 500 puntuko irudia aukeratu zuten, 8 byteko kolore grisen eskalan. Horrek hatz-marken fitxa bakoitzetik 10MBko fitxategi bat sortzen zuen. Artxibo osoaren digitalizazioak izugarrizko tamaina hartu behar zuen! Gainera, duela 25 urteko tresnen biltegiratze-gaitasuna gaurkoena baino askoz txikiagoa zen. Zer egin? Aurreko artikulu batean argazkietarako esan genuen moduan, hemen ere konpresioan zegoen gakoa. Gogoan izan konprimatzea fitxategiaren tamaina txikitzea dela eta hori, baliagarria izateko, informazio esanguratsua galdu barik egin behar dela.

Argazkietarako azaldu genuen JPEG konpresio-sistema 1992an kaleratu zen eta horixe erabiltzeko hautua egin zuten FBIko adituek. Hala ere, ez ziren gustura gelditu, konprimatu ondoko irudia ez baitzitzaien egokia iruditu.

Gehienetan, pixel batetik albokora igarotzean kolore-aldaketa txikia egoten da eta hori baliatzen du JPEG sistemak. Horregatik, ertzak dauden tokietan emaitza ez da hain ona, inguruko pixeletan kolore-aldaketa handiak gerta daitezkeelako. Esan daiteke, neurri batean, hatz-marken irudietan ertzak (marrak) direla garrantzia duten bakarrak.

Arazoa gainditzeko, Estatu Batuetako zenbait unibertsitate eta gobernu-agentziatako ikertzaile elkarlanean aritu ziren hatz-marken irudien konpresiora egokitutako algoritmo on baten bila.

Bitarte matematikoa

1984an Yves Meyer matematikari frantsesa Paris-Orsay unibertsitateko irakaslea zen. Lankide fisikari batek artikulu bat erakutsi zion, interesgarria izango zitzaiolakoan. Egileak Jean Morlet eta Alex Grossmann ziren, Elf Aquitaine enpresako ingeniari geofisikaria lehena eta Marseillako unibertsitateko fisikaria bigarrena.

Artikuluak gasa eta petrolioa bilatzeko bide berri bat proposatzen zuen. Lur azpiko gas-poltsak eta petrolioa detektatzeko, uhin bat igortzen da eta zenbait geruza zeharkatu ondoren itzultzen den seinalea aztertuz, barneko konposizioari buruzko informazioa lortzen da. Morletek hori egiteko teknika berri bat aurkeztu zuen eta Grossmannekin landu zuen arlo matematikoa. Ez zuen arrakasta handirik izan enpresan eta, diotenez, Morletek jubilazio aurreratua baino ez zuen lortu. Aitzitik, zientziaren mundutik iritsi zitzaion ospea.

Yves Meyer harrituta gelditu zen artikuluan ikusi zuenarekin: formula ezagunak aurkitu zituen, ederto ezagutzen zuen alor batekoak, eta bide emankorra izan zitekeela iritzi zion. Berak dioenez, Marseillarako trena hartu zuen Grossmannen bila. Urte gutxiren buruan, Meyer eta haren lankide eta ikasleek hasierako urrats baldar haiek teoria matematiko bihurtu zuten.

Fourieren teoria klasikoan funtzio bat garatzeko oinarrizko osagaiak funtzio trigonometrikoak dira. Teoria berrian, oinarrizko osagai horiek aldatu egiten dira eta funtzio ama baten dilatazioak eta translazioak erabiltzen dira. Hori bai, ama horrek propietate egokiak behar ditu erabilgarria izateko. Dena dela, aukera asko daude eta erabileraren arabera zein hartu erabaki daiteke. Horixe bera abantaila bihurtzen da aplikazioetan.

Objektu berriari frantsesez jarri zion izena Morletek: ondelette. Gero, ingelesera heldu zenean, wavelet bihurtu zen eta gehienbat horrela egin du bidea mundu zientifikoan. Erabiltzaile askok mailegua bere horretan (wavelet) hartu badute ere, badira hizkuntza bakoitzari egokitutako terminoak: ondícula (esp.), ondeta (cat.), onduleta (port.), adibidez. Euskaraz, horien antzeko izan daitekeen uhinxka hautatu nuen nik [1].

Fourieren analisi tradizionalak ez ditu ondo antzematen tarte txiki batean gertatzen diren funtzio baten aldaketa handiak, osagai modura erabiltzen dituen funtzio trigonometrikoak ez daudelako lokalizatuta. Uhinxkak, aldiz, lokalizatu egiten dira eta hobeto moldatzen dira funtzioen aldaketa zorrotzak aztertzeko. Gainera, zertan erabili nahi dugun, uhinxka ama egokia hartzea komeni da. Horrek kostu matematiko handiagoa izan dezake eta, aplikatzeko bada, agian kostu ekonomikoa ere, baina nahi edo behar dugun lana hobeto egingo du.

WSQ eta JPEG2000 konpresio-sistemak

Uhinxken teoriak, aurrekari zuen Fourieren serieen teoriak ez bezala, aldi berean jorratu ditu arlo matematiko hutsa eta aplikazioak. Berehala hasi ziren seinaleen prozesamendurako erabiltzen eta ohiko teknikak arlo berrira egokitu ziren. Lehen urrats haietatik mundu errealerako jauziak ez zuen itxaron behar izan. Are gehiago, teoria matematikoa bera elikatu dute aplikazioek, problema berriak plazaratuz.

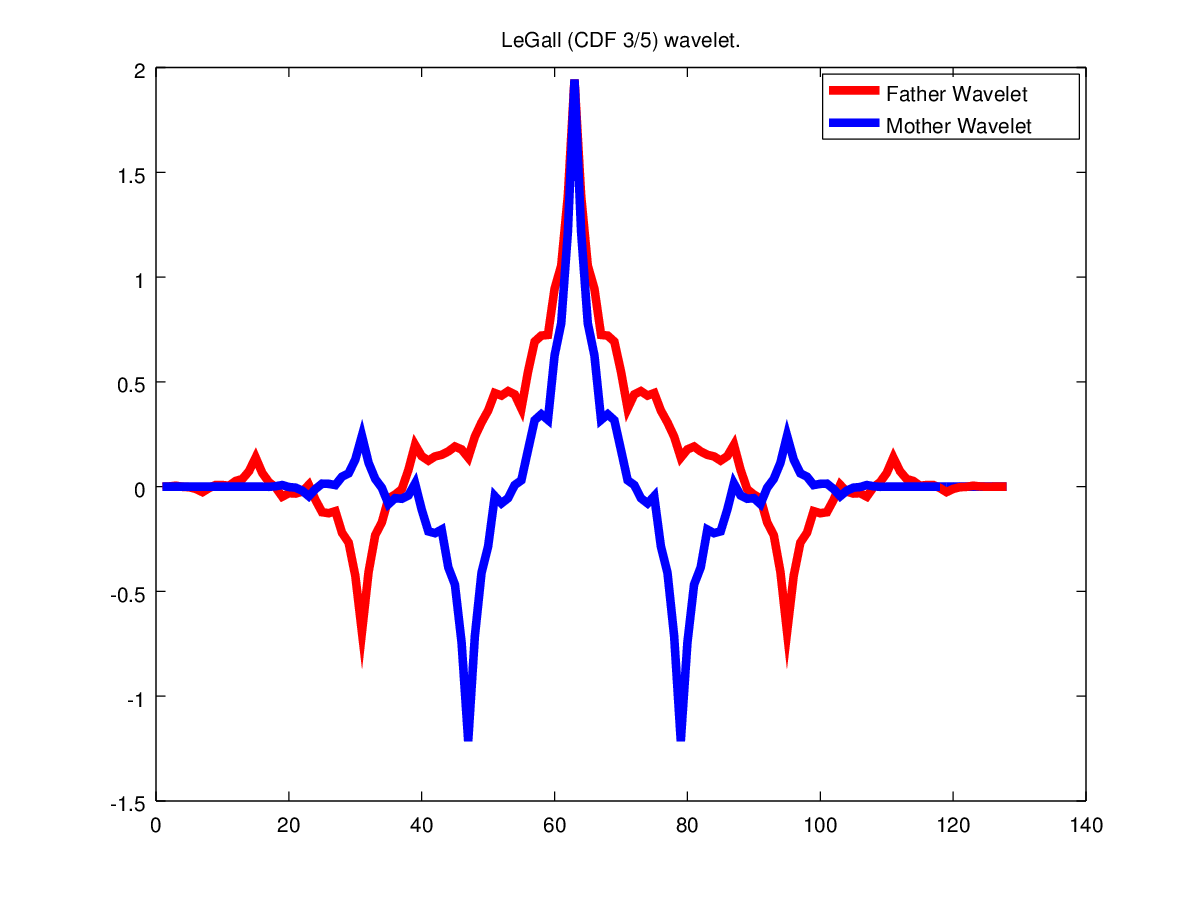
Uhinxkak erabilita asmatu zuten FBIren beharretarako WSQ (Wavelet Scalar Quantization) konpresio-sistema. Libre jarri zuten, gainera, edozeinek erabiltzeko moduan. Matematikoki uhinxka amen bikote bat erabiltzen du, bata deskonposizioa egiteko, eta bigarrena irudia berreraikitzeko. Funtsean, konpresiorako gauza bera egiten da beti: gorde nahi dugun informazioa oinarrizko osagaien (kasu honetan, uhinxken) errezeta baten bidez eman eta garrantzi gutxiko osagaien koefizienteak 0 egin. Horrela, gorde beharreko informazioan 0 asko lortzen dira, eta zeroen zerrenda horiek modu laburrean gordetzeko bideak asmatu dira.

Ez zen horretan geratu uhinxken konpresiorako erabilera. Argazkietarako JPEG asmatu zuen talde berak beste estandar bat sortu zuen uhinxken bidez: JPEG2000. Hau ere erabiltzen da hatz-marken konpresiorako, hazbeteko 1000 puntuko irudiak hartzen direnean. Eta ez horretarako bakarrik: JPEG2000 erabiltzen da zinema digitalean, sateliteek hartzen dituzten irudietan eta irudi medikoen DICOM protokoloan, esaterako.

Fourier modernoa vs. Fourier klasikoa

Fourieren analisia matematika teorikoaren esparruan bizi zen XIX. mendean eta XX. mendearen hasieran. Gero, ordea, mundu errealean erabiltzeko arlo ugari aurkitu zizkioten eta ordenagailuen kalkulu-ahalmena handitzearekin batera are gehiago zabaldu ziren aukerak: seinaleak, soinuak, irudi medikoak, espektrometria, kristalografia, telekomunikazioa, astronomia, ikusmen artifiziala, ahots-ezagutzea…

Uhinxken teoriak, geuk sortzen eta garatzen ikusi dugun arlo berriak, beste bultzada bat eman die aplikazioei. Aipatu dugun hatz-marken kasuan, bide klasikoak baino emaitza hobeak ematen ditu. Beti mereziko du uhinxkak erabiltzea funtzio trigonometrikoen ordez? Ez, egin nahi dugunaren arabera erabakiko dugu. Esaterako, gure argazki-kameretan JPEG erabiltzen dugu, ez du merezi argazki arruntetarako beste konpresio-sistema batera jotzea. Teoria berriak aurrekoa osatu egiten du, ez ordezkatu.

Matematikan gaur egun dagoen saririk handiena Abel saria da. 2017ko saritua Yves Meyer izan zen, “haren funtsezko lanagatik, uhinxken teoria matematikoaren garapenean”.

Oharrak

[1] Norbaitek mailegua erabili nahiko balu, jatorrizko frantses izenetik hartutako ondeleta hobetsiko nuke, zaila egiten baitzait wavelet euskaraz modu egokian ematea.

Gehiago jakiteko

• Hatz-markak eta FBI: C. M. Brislawn, Fingerprints go digital, Notices of the American Matematical Society 42, 1995.
• Uhinxkak Mathouriste webgunean: Après Fourier, c’est encore du Fourier! Fourieren analisiari buruzko informazio ugari dago, historikoa besteak beste, web guneko hainbat orrialdetan.
• Abel saria 2017: uhinxkak eta Yves Meyer, zer irakurri eta zer ikusi asko dago web gune horretan.
• Hatz-markei buruzko artikulu bat Zientzia Kaieran (2015): Hatz-markak aldatzen dira denborarekin, baina ez hainbeste.

---

Egileaz: Javier Duoandikoetxea Analisi Matematikoko Katedraduna da UPV/EHUn.

---