Moritz Abraham Stern (1807-1894) lehenengo lerroko matematikari alemaniar bat izan zen ([1]),eta bere doktorego tesiaren zuzendaria Carl Friedrich Gauss (1777-1855) matematikari aski ezaguna izan zen. Stern-en lan ezagunen artean Stern-en segida izena duena dago ([2], ikus 1 Taula).
Modu bakun errekurtsibo honen bitartez defini daiteke:
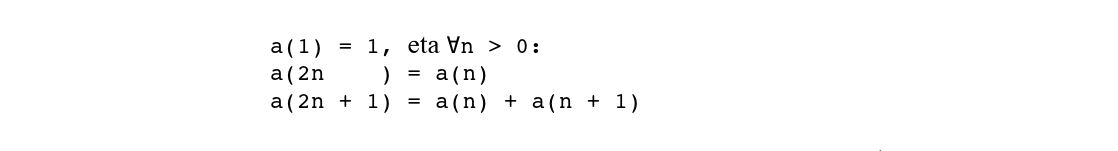
Segida honek garrantzia du, besteak beste, zenbaki arrazional positiboen (ℚ+) hainbat zenbakitze sistemaren oinarrian dagoelako. Esate baterako, Calkin-Wilf-en zenbakitze sistemaren oinarrian [3]: a(n) bada Stern-en segidaren n. gaia, a(n)/a(n+1) (n > 0) zatiki-segidak zenbaki arrazional positibo guztien segida osatzen du, bat ere errepikatu gabe.
Stern-en segida The On-Line Encyclopedia of Integer Sequences (OEIS)-en A002487 etiketaduna da [4]. Bertan ikus daitezke hainbat ikerlarik aurkitu dizkioten hainbat propietate, formula, konputazio-programa, eta beste zenbait segidarekin dituen loturak eta erreferentziak, bai eta beste zenbait problema matematikoei buruzko iruzkinak ere. Webgunea etengabe ari da berritzen eta
hazten.
Problema matematiko bat da segidaren n. gaiaren balioa (a(n), n > 0) ahalik eta azkarren kalkulatzea; hau da, definizio-formularen errekurtsibitatea arintzea. Propietate berri bat burutu da, bai eta horretan oinarrituta problemari soluzio bat ematen dion algoritmo bat ere. Propietate berria enuntziatu aurretik n zenbaki arruntaren adierazpide mota bat aurkeztu behar da:
∀n > 0, ∃1m ≥ 0, eta ∃1k 0 ≤ k < 2m, n = 2m + k delarik.
Horrela, segidaren a(n) balioak a(2m+k)-ren bitartez azalduko dira. Adierazpide honen arabera definizio-formula hauxe da:
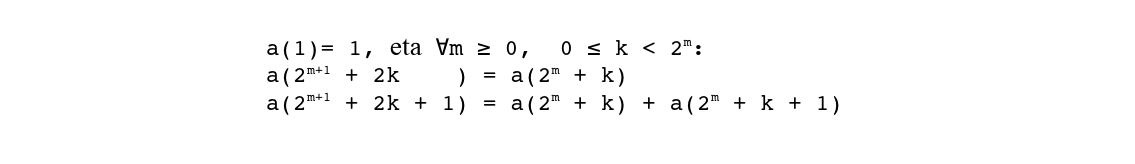
1 Taulako segidan a(n) balioak 2m gaika (m ≥ 0) pilatzen badira ezkerraldean, egitura triangeluar bat osatzen da (ikus 2 Taula).
Modu honetan azalduta, segidaren propietate batzuk nabarmenak dira. Lerroka begiratuta:
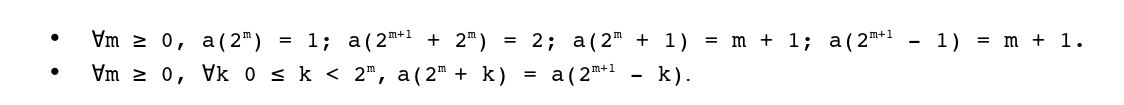
Zutabeka begiratuta, zutabe bakoitzean segida aritmetiko bat ikusten da, eta diferentzien segida Stern-en segida bera da (ikus 3 Taula).
Aurkitutako erlazio hau honela zehaztu daiteke:
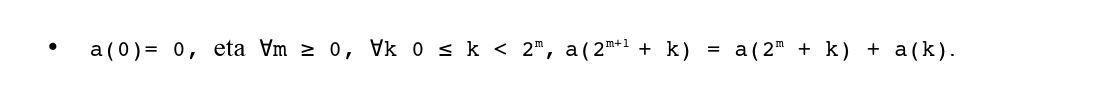
Ohar daitekeenez, segidari beste gai bat gehitu behar izan zaio: a(0)= 0, 2 Taulan agertzen ez dena.
Propietate berria ez da hain nabarmena, baina 3 Taularen zutabekako segida aritmetikoetan oinarritzen da ere.
Adibidez, k = 27:
Orokorrean honela enuntzia daiteke:
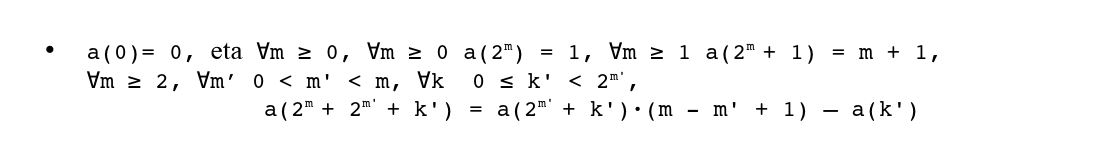
Stern-en segidaren propietate errekurtsibo berria esperimentalki induzitu egin da, bai eta matematikoki bere egiazkotasuna frogatu ere.
Bi formula errekurtsiboak alderatzean ikusten da definizio-formularen errekurtsibitatea datzala 2 Taularen maila batetik ondoz ondoko mailara igarotzean ((m+1)-tik m-ra), eta propietate berriarenean, aldiz, maila batetik aurreko beste maila batetara igarotzean (m-tik m’-ra, m’ < m); hau da, propietate berriaren errekurtsibitatean jauzi handiagoak gerta daitezke, eta ondorioz azkarrago izango da, orokorrean, a(n)-ren balioa kalkulatzea.
Formula edo propietate berri hori garatuz gero, errekurtsiboki (goitik behera, top-down, m handitik txikira), n-ren adierazpide bitarrean oinarritzen den algoritmo bat lortzen da, eta segidaren
hasierako a(0) = 0 eta a(1) = 1 balioak nahikoak dira algoritmoa abiatzeko.
Adibidez:
Beraz, 91-ren adierazpide bitarrean oinarritzen diren cj (1 ≤ j < 5) biderkagaiak kalkulatuz (‘1’ekoen arteko jauziak hartzen dira kontuan), eta egokiro konbinatuz gero (behetik gora, bottom-up), nahikoa da a(91)-ren balioa emateko.
Orokorrean:
Ondorengo biderkagaiek n-ren adierazpide bitarra jartzen dute jokoan. b = 1 baldin bada (‘1’-eko bakarra), orduan bedi c1 = 1 (∀m ≥ 0, a(2m) = 1 delako), eta bestela:
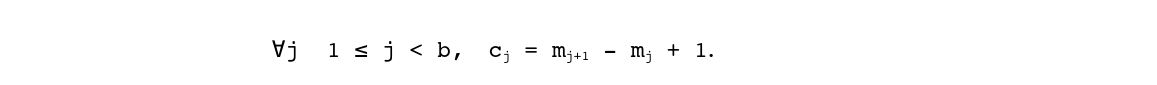
Biderkagai hauek ‘1’-ekoen artean dauden jauziak adierazten dituzte.
Bedi f burututako formula errekurtsibo berria islatzen duen funtzio errekurtsiboa:
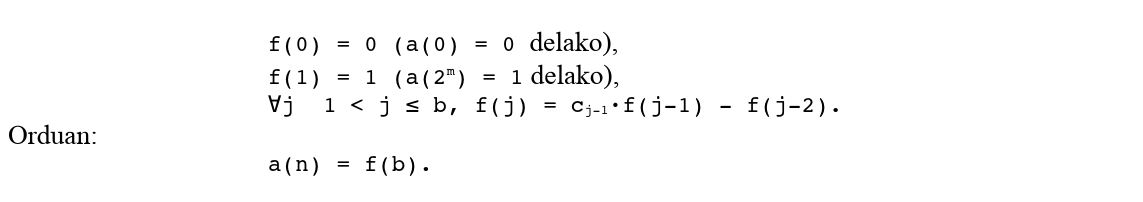
Adibidean:
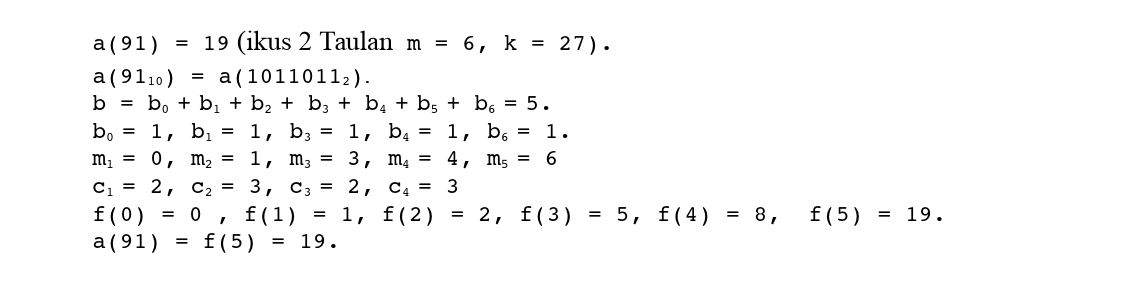
Ondorioz, eraikitako algoritmoa konputazionalki askoz ere azkarragoa da definizio-formulan oinarritutakoa baino.
Stern-en segidaren propietate berri bat esperimentalki induzitu da, eta matematikoki haren egiazkotasuna frogatu. Formula horretan oinarrituz segidaren edozein tokitako balioa kalkulatu daiteke eta eraikitako algoritmoa konputazionalki azkarragoa da definizio-formulan oinarritutakoa baino. Algoritmo hori n-ren adierazpide bitarrean oinarritzen da.
Erreferentzia bibliografikoak:
[1] O’Connor, J. J., Robertson, E. F., (2018). MacTutor History of Mathematics archive, School of Mathematics and Statistics. University of St Andrews, Scotland.
[2] Stern M. A., (1858). Über eine zahlentheoretische Funktion. Journal fur die reine und angewandte Mathematik, 55, 193-220.
[3] Calkin, N., Wilf, H., (2000). Recounting the Rationals. American Mathematical Monthly, 107 (4), 360-363. DOI: https://www.math.upenn.edu/~wilf/website/recounting.pdf.
[4] SLOANE N. J. A. 2018. The On-Line Encyclopedia of Integer Sequences (OEIS) (founded in 1964). https://oeis.org/A002487.
Iturria:
Artikuluaren fitxa
- Aldizkaria: Ekaia
- Zenbakia: Ekaia 35
- Artikuluaren izena: Stern-en segidaren propietate berri bat eta segidaren n. gaia azkar kalkulatzeko algoritmo bat
- Laburpena: Stern-en segida zenbaki arruntez osatuta dago, eta propietate asko ditu. Segidaren propietate berri bat azaltzen da lan honetan, hain zuzen segidaren n. gaia zein den azkar kalkulatzeko balio duena. Azkartasun hori n-k sistema bitarrean duen adierazpidean oinarritzen da. Propietatea nondik nora sortu den azaltzen da, baita haren egiazkotasunaren froga matematikoa ere.
- Egileak: Yosu Yurramendi Mendizabal
- Argitaletxea: UPV/EHUko argitalpen zerbitzua.
- ISSN: 0214-9001
- eISSN: 2444-3255
- Orrialdeak: 325-339
- DOI: 10.1387/ekaia.19513
Egileez
Yosu Yurramendi Mendizabal UPV/EHUko Informatika fakultateko Konputazio Zientziak eta Adimen Artifiziala sailean dabil.
Ekaia aldizkariarekin lankidetzan egindako atala.
