- Anartzek: “bikoitia da eta 3ren multiploa”.
- Garik: “3ren multiploa da eta azken zifra 5 da”.
- Mikelek: “5en multiploa da eta zifren batura 12 da”.
Zenbat balio desberdin har ditzake zenbakiak?
Zenbakia 3ren multiploa ez bada, Anartzen eta Gariren egiak “bikoitia da” eta “azken zifra 5 da” izango lirateke. Baina horiek ez dira bateragarriak eta, ondorioz, zenbakia 3ren multiploa da. Gainera, zenbakia ez da bikoitia eta azken zifra ez da 5, beraz ezin daiteke 5en mutiplo izan. Orduan, Mikelen egia zifren batura 12 dela da. Hortaz, zifrak 3 eta 9 edo 5 eta 7 dira, eta zenbaki posibleak 39, 93 eta 57. Hiru balio desberdin, beraz.
Koldotxuren erantzuna zuzena da eta argi arrazoituta.
2. Zenbat modutan har daitezke pizzaren zortzi zatietatik hiru, elkarren alboko bi hartu barik?
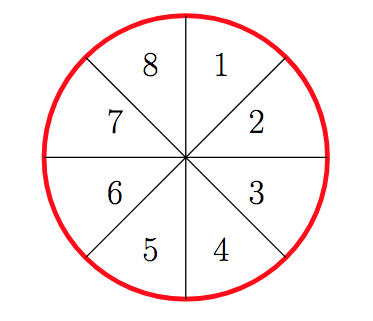
Pizza zati bakoitza 6 modutan aukera daiteke. Esate baterako, 1 zatia hartuz gero, hauek dira aukerak: 1-3-5, 1-3-6, 1-3-7, 1-4-6, 1-4-7 eta 1-5-7.
Zati bakoitza 6 modutan aukeratuta, zortzi zati direnez, 48 aukera dira denetara. Aukera bakoitza hiru bider hartzen ari garenez, 48 : 3 = 16 dira benetan modu desberdinak.
Nahi izanez gero, aukera guztien zerrenda eman daiteke eta horrek beste ebazpide bat ematen du. Goian daude 1 zatia hartuta agertzen diren 6 aukerak. 2 zatia sartzen badugu, beste sei: 2-4-6, 2-4-7, 2-4-8, 2-5-7, 2-5-8 eta 2-6-8. 3 sartuta eta ez 1, beste hiru daude: 3-5-7, 3-5-8 eta 3-6-8. Azkenik, 4 sartuta eta ez 1 ez 2, beste aukera bat: 4-6-8. Eta ez dago gehiago, ez badugu 1, 2, 3 edo 4 hartzen, ez dago baldintza betetzeko modurik.
Joseluk ariketaren erantzun zuzena utzi digu eta, gainera, kasu orokorrerako formula ere eman digu, hau da, pizzaren zatiak 8 izan beharrean, n direnerako.
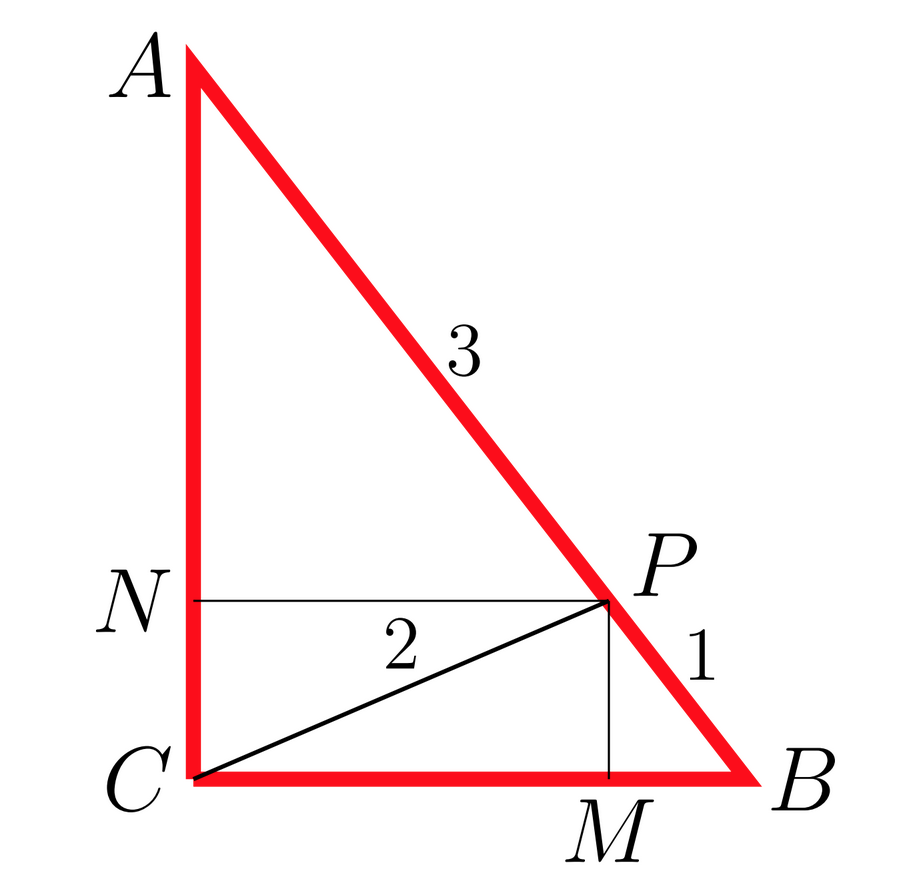
Egin ditzagun katetoen paraleloak P puntutik. Horrela, irudiko M eta N puntuak lortuko ditugu. PMB, ANP eta ACB triangeluak antzekoak dira, hau da, angelu berdinak eta alde proportzionalak dituzte. Orduan,
PM = AN/3 = AC/4 eta MB = NP/3 = CB/4.
Idatz dezagun MB = x eta PM = y. Pitagorasen teorema erabiliz PMB eta PMC triangelu zuzenetan,
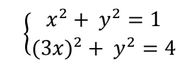
Hortik, 8x2 = 3, hots, x2 = 3/8, eta y2 = 5/8 lortzen dira. Katetoen luzerak, beraz, hauek dira:
![]()
Joseluk utzi digu erantzun zuzena.
Izan bedi x kakao kutxa baten eroste-prezioa. Irabazia 0.2 x izango da.
Demagun N kakao kutxa eta 2N kafe kutxa saldu direla. (Berez, N zein den berdin da, baina jarrai dezagun horrela.) Erostean, 200 N + N x ordaindu dugu. Irabaziak 80 N + 0.2 N x dira. Denetara % 36 irabazi dugunez,
80 N + 0.2 N x = 0.36 (200 N + N x).
Bistan da N sinplifika daitekeela eta ekuazio hau gelditzen dela: 8 = 0.16 x. Hemendik, x = 50 aterako dugu. Hori da, beraz, kakao kutxaren prezioa erosten dugunean. % 20ko irabazia gehituta, 60 euroan saldu da.
Berriro ere, Joseluk eman digu erantzun zuzena. Ez hori bakarrik, hiru bide utzi dizkigu erantzuna lortzeko.
Izan bitez N lagun denetara, Markel barne. Bakoitzak 756/N gerezi hartu ditu. Hiru lagunek gereziak eman dizkiote Markeli, bakoitzak 756/4N, hau da, 189/N = 3 x 3 x 3 x 7/N. Zenbaki horrek osoa eman behar du eta N gutxienez 4 da (Markel eta hiru lagun). N = 7 bada, Markelek 189 gerezi jan ditu (108 + 27 + 27 +27). N = 9 izanda, 147 jango lituzke (84 + 21 + 21 + 21) eta hori ez da onargarria. Are gutxiago jango lituzke, lagunak gehiago balira. Beraz, 7 lagun dira eta Markelek 189 gerezi jan ditu.
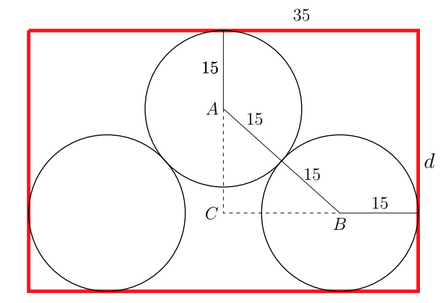
Zirkuluak irudiak erakusten duen moduan daude (alde bertikalak beherago etor daitezke, baina d-ren balio txikiena irudikoa da).
Alde batetik, CB + 15 = 35 daukagu. Hortik, CB = 20 aterako dugu. ABC triangeluan Pitagorasen teorema erabiliz, AC2 = 302 – 202= 500 lortuko dugu, hau da, ![]() . Orduan, d-ren balio txikiena AC + 30 denez,
. Orduan, d-ren balio txikiena AC + 30 denez, ![]() lortuko dugu.
lortuko dugu.
Azken ariketa bietarako ez dugu erantzunik jaso, idazten ari naizen egunera arte (irailaren 13a).
Egileaz:
Javier Duoandikoetxea Analisi Matematikoko Katedradun erretiratua da UPV/EHUn.