Algoritmo kriptografiko ezagun bat eguneratu dute

Bi ikertzailek sareten oinarriak laburtzeko oso ezaguna den teknika bat hobetu dute; eta, horren bidez, bide berriak ireki dituzte kriptografiaren eta matematikaren arloan esperimentu praktikoak egiteko.

Gure bizitzak gero eta digitalagoak dira, eta segurtasuna kriptografiaren menpe dago. Mezu pribatu bat bidaltzean edo faktura bat online ordaintzean, gure datuak sekretupean mantentzeko diseinatutako algoritmoen menpe gaude. Baina jakina, pertsona batzuek sekretu horiek deskubritu nahi dituzte. Hori dela, ikertzaileek sistema horien sendotasuna probatzeko lan egiten dute, erasotzaile adimentsu batek eskua sartzen duenean erori ez daitezen.

Lan horretarako ezinbesteko tresna da LLL algoritmoa (1982an argitaratu zuten ikertzaileen izena darama: Arjen Lenstra, Hendrik Lenstra Jr. eta László Lovász). LLL eta haren ondoko sistema guztiek trikimailu kriptografikoak desegin ditzakete zenbait kasutan. Hori dela eta, ikertzaileentzat oso lagungarria da sistema horien jokabidea aztertzea, erasoen aurrean hain ahulak ez diren sistemak diseinatu ahal izateko. Algoritmoaren talentuak kriptografiaz harago doaz, baina; izan ere, matematika eremu aurreratu batzuetan ere tresna erabilgarria da, hala nola zenbakien teoria konputazionalean.

Urteetan zehar, ikertzaileek LLLren barianteak hobetu dituzte, ikuspegi praktikoagoa izateko, baina soilik puntu batera arte. Oraingo honetan, berriz, bi kriptografok LLL estiloko algoritmo berri bat sortu dute, eta askoz ere efizienteagoa da. Teknika berri horrek artikulu onenaren saria irabazi zuen 2023ko Kriptologiako Nazioarteko Konferentzian; izan ere, nabarmen areagotu du informatikariek eta matematikariek LLLren antzeko ikuspegiak erabil ditzaketen agertokien zerrenda.

«Benetan hunkigarria izan zen», adierazi zuen Chris Peikertek, Michigango Unibertsitateko kriptografoak (hark ez zuen artikuluan parte hartu). «Tresna hori aztergai izan dugu hamarkadetan zehar», esan zuen. «Oso atsegina da hainbeste urtetan landutako helburua lortu izana… Horrek frogatzen du oraindik ere sorpresa asko daudela deskubritzeko».

LLL motako algoritmoak sareten esparruan erabiltzen dira: erregularki tartekatutako puntuen bilduma infinituak. Ondo irudikatzeko, pentsa dezagun zoruan baldosak jartzen ari garela. Baldosa karratuz estal genezakeen dena eta, orduan, baldosen izkinek sareta bat osatuko lukete. Txandaka, baldosa ezberdinak jar ditzakegu (adibidez, paralelogramo luzanga bat), beste mota bateko sareta bat sortzeko.

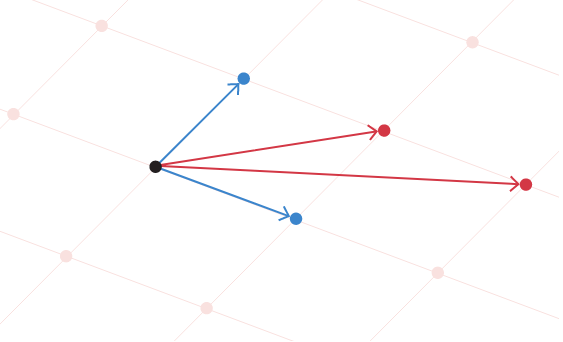
Sareta bere «oinarria» erabilita deskriba daiteke. Oinarri hori bektoreen multzo bat da (nagusiki, zenbaki zerrendak); eta horiek hainbat modutan konbina daitezke saretaren puntu bakoitza lortzeko. Imajinatu bi bektore hauek osatutako oinarria duen sareta bat: [3, 2] eta [1, 4]. Sareta bektore horien kopien batuketak eta kenketak eginez lor ditzakegun puntu guztiak dira.

Baina bektore bikote hori ez da saretaren oinarri bakarra. Gutxienez bi dimentsio dituen sareta orok oinarri posible infinituak ditu. Baina oinarri guztiak ez dira berdinak. Oinarriaren bektoreak laburragoak eta haien artean angelu zuzenengandik hurbilagoak direnean, errazagoa da lantzeko, baita erabilgarriagoa ere problema konputazional batzuk ebazteko ere. Hori dela eta, ikertzaileentzat oinarri «onak» dira horiek. Horren adibide da jarraian agertzen den figurako bektore bikote urdina. Aitzitik, bektore luzeagoak eta ez hain ortogonalak dituzten oinarriak (bektore gorriak, adibidez) «txarrak» izango liratekeen.

Azken hori LLL bidez lantzeko kontua da: emaiozu hari (edo haren antzeko sistemaren bati) sareta multidimentsional baten oinarria eta hobeago bat aurkituko du. Prozesu horri sareten oinarria laburtzea esaten zaio.

Eta, zer lotura du horrek guztiak kriptografiarekin? Bada, sistema kriptografiko bat hausteko lana, zenbait kasutan, beste problema baten gisan birformulatu daiteke: sareta batean erlatiboki laburra den bektore bat aurkitzea. Eta, batzuetan, bektore hori LLL estiloko algoritmo batek sortutako oinarri laburtutik atera daiteke. Estrategia horren bidez, ikertzaileek itxuraz saretekin lotura handia ez duten sistemak eraitsi ahal izan dituzte.

Zentzu teorikoan, jatorrizko LLL algoritmoa arin batean exekutatzen da: exekutatzeko behar den denborak ez du esponentzialki eskalatzen sarreraren tamainarekin; hau da, oinarriko bektoreen zenbakien tamaina (bits-etan) eta saretaren dimentsioa. Hala ere, funtzio polinomiko gisa areagotzen da, eta “benetan egin nahi baduzu, denbora polinomikoa ez da beti hain posiblea”, azaldu zuen Léo Ducasek, Herbeheretako CWI ikerketa institutu nazionaleko kriptografoak.

Praktikan, horrek esan nahi du jatorrizko LLL algoritmoak ezin dituela handiegiak diren sarrerak gobernatu. “Matematikari eta kriptografoek gehiago egiteko ahalmena izan nahi zuten”, esan zuen Keegan Ryanek, Kaliforniako Unibertsitateko (San Diego) doktoregoko ikasleak. Ikertzaileak lanean aritu dira LLL estiloko algoritmoak optimizatzeko, sarrera handiagoak erabili ahal izateko; eta, askotan, errendimendu ona lortu dute. Hala ere, eginkizun jakin batzuk lortzeko ezinezkoak ziruditen.

Artikulu berriak, Ryanek eta bere tesi zuzendari Nadia Heningerrek idatzitakoak, askotariko estrategiak konbinatzen ditu LLL estiloko beren algoritmoaren efizientzia hobetzeko. Alde batetik, teknikak egitura errekurtsibo bat erabiltzen du, eginkizuna zati txikiagotan banatzen duena. Bestetik, algoritmoak kontu handiz kudeatzen du tartean dauden zenbakien doitasuna, abiaduraren eta emaitza zuzenaren arteko oreka lortuta. Lan berriari esker, ikertzaileek milaka dimentsiotako sareten oinarriak laburtu ahal dituzte.

Aurreko lan batzuek ere ikuspegi bera izan zuten: 2021eko artikulu batek ere errekurtsibitatea eta doitasunaren kudeaketa konbinatu zituen sareta handiekiko lana arintzeko, baina soilik funtzionatzen du sareta mota zehatzetarako, eta ez kriptografian garrantzitsuak diren guztietarako. Algoritmo berriak ondo funtzionatzen du tarte askoz handiagoan. «Oso pozik nago norbaitek lortu duelako», esan du Thomas Espitauk, PQShield enpresako kriptografiako ikertzaile eta 2021eko bertsioaren egileetako batek. Bere taldeak “kontzeptu proba” bat eskaini zuen; eta emaitza berriak erakutsi du «sareta baten laburpena arin eta modu sendoan egin daitekeela».

Teknika berria erabilgarri suertatu da jada. Aurel Pagek, Frantziako INRIA ikerketa institutu nazionaleko matematikariak, esan du bere taldearekin batera algoritmoaren egokitzapen bat abiarazi duela zenbakien teoriako eginkizun konputazional batzuetan.

LLL estiloko algoritmoek, halaber, rol garrantzitsua bete dezakete seguru mantentzeko diseinatutako saretetan oinarrituta dauden kriptografia sistemekin lotutako ikerketan; baita, etorkizunean, ordenagailu kuantiko handiekin ere. Ez dira horrelako sistementzako mehatxua; izan ere, horiek eraisteko algoritmoek aurkitzen dituztenak baino bektore laburragoak aurkitu behar dira. Alabaina, ikertzaileentzat ezagun diren erasorik onenek LLL estiloko algoritmo bat erabiltzen dute “oinarrizko elementu” gisa. Halaxe azaldu zuen Wessel van Woerdenek, Bordeleko Unibertsitateko kriptografoak. Eraso horiek aztertzeko esperimentu praktikoetan, oinarrizko elementu horrek prozesu osoa motel dezake. Tresna berriarekin, aldiz, ikertzaileek eraso algoritmoekin exekutatu ahal diren esperimentuen sorta zabalduko da, errendimenduaren irudi argiagoa eskuratuta.

Jatorrizko artikulua:

Madison Goldberg (2023). Celebrated Cryptography Algorithm Gets an Upgrade, Quanta Magazine, 2023ko abenduaren 14a. Quanta Magazine aldizkariaren baimenarekin berrinprimatua.

Itzulpena:

UPV/EHUko Euskara Zerbitzua.