Aurten ere, hamar urteren ostean, erantzun asko izan ditugu eta gehienak zuzenak. Eskerrik asko parte hartu duzuen guztioi. Eta eskerrik asko ere zuen artean animatzen eta elkarri laguntzen ibili izanagatik.
Ane eta beste bederatzi lagun mahai baten bueltan jarrita daude. Bakoitzak zenbaki bat pentsatu du eta alboko lagun biei isilean esan die. Ondoren, bakoitzak boz goraz esan du bere alboko bien zenbakien batezbestekoa. Ane hasi da eta 10 esan du. Haren ezkerrekoak 9 esan du eta, ezkerrerantz jarraituz, hurrengoak 8, gero 7, eta horrela, beti bat gutxiago, Aneren eskuineko lagunak 1 esan duen arte. Zein da Anek pentsatu duen zenbakia?
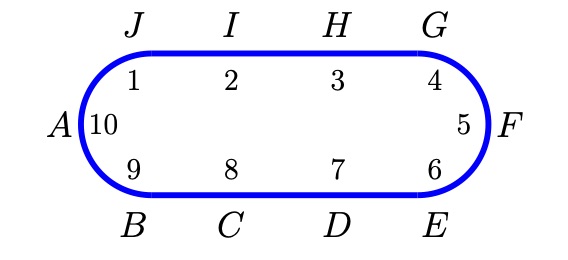
Irudian agertzen dira A(ne) eta haren lagunak, bakoitzak boz goraz esan duen zenbakiarekin. Zenbaki horren bikoitza da alboko biek pentsatu duten zenbakien batura. Horrela,
A + C = 18, E + G = 10 eta I + A = 2,
eta denak batuta, 2A + C + E + G + I = 30. Era berean,
C + E = 14 eta G + I = 6, hau da, C + E + G + I = 20.
Aurrekotik kenduta, 2A = 10, eta A = 5 lortzen da, Anek pentsatu duen zenbakia.
Nahi izanez gero, besteen zenbakiak ere eman daitezke. Goiko ekuazioetatik hauek ateratzen dira: C = 13, E = 1, G = 9 eta I = -3. Beste bostak lortzeko era berean joka dezakegu. Balio hauek ateratzen dira: B = 14, D = 2, F = 10, H = -2 eta J = 6.
Irudiko laukizuzenaren alde luzeak 25 cm du eta karratuaren aldeak, 20 cm. Zein da laukizuzenaren alde txikiaren luzera?
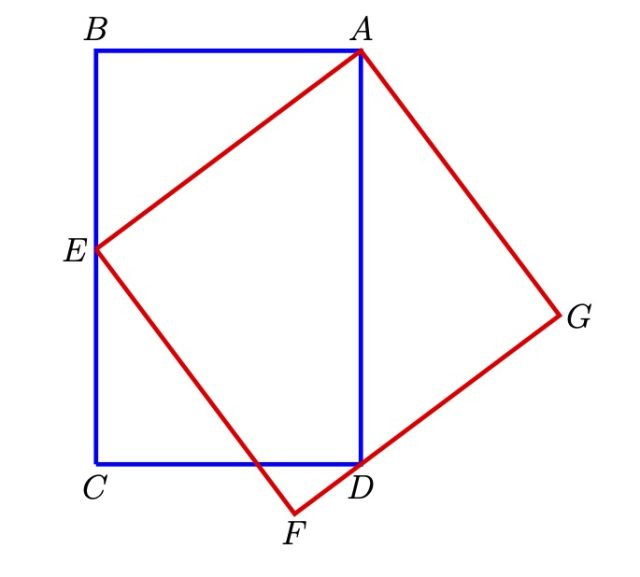
A erpineko hiru angeluri begiratuko diegu. Horietatik bi, ang(BAE) eta ang(DAG), berdinak dira, biei ang(EAD) gehituta angelu zuzena lortzen delako. Horren ondorioz, ABE eta ADG triangeluak antzekoak dira (angelu berdinak dituzte) eta aldeak proportzionalak izango dira:
AG/AD = AB/AE edo 20/25 = AB/20.
Hortik, AB = 16 cm lortzen dugu.
Segida baten lehen hiru gaiak 1, 2 eta 3 Hortik aurrera, gai bat lortzeko haren aurretik dauden hirurak hartzen dira kontuan, horietako lehen bien baturari hirugarrena kenduta. Adibidez, laugarrena 1 + 2 – 3 = 0 izango da; bosgarrena, 2 + 3 – 0 = 5, eta abar. Formalki n. lekuko gaia anbada, an = an-3 + an-2 – an-1 . Horrela, segidaren hasiera 1, 2, 3, 0, 5, -2, 7… da. Zein izango dira 2024. eta 2025. postuetan agertzen diren gaiak?
Har ditzagun segidan jarraian datozen lau gai, edozein tokitan kokatuta: A, B, C eta D izendatuko ditugu. Enuntziatuak dio D = A + B – C dela edo, bestela idatzita, C – A = B – D. Hau da, lehenengotik hirugarrenera pasatzeko eta bigarrenetik laugarrenera pasatzeko kopuru bera gehitzen da, baina zeinua aldatuta. Hori segidaren edozein tokitan. (Bide batez, esan dezagun segidaren gaiak binaka hartuta bien batura konstante mantentzen dela, A + B = C + D delako.)
Segidaren lehen gaitik (1) hirugarrenera (3) 2 gehitu dugunez, bigarrenetik laugarrenera -2 gehituko dugu, eta orduan, hirugarrenetik bosgarrenera ere 2 gehituko dugu, eta laugarrenetik seigarrenera -2, eta abar. Bestela esanda, posizio bakoiti batetik hurrengo bakoitira 2 gehituko dugu, eta posizio bikoiti batetik hurrengo bikoitira, -2. Hortaz, segidaren posizio bakoitietan dauden gaiak 1, 3, 5, 7, 9, 11… izango dira (posizioaren balio bera) eta posizio bikoitietan, 2, 0, -2, -4, -6, -8… (posizioaren balioari 4 kendu eta zeinua aldatu).
Ondorioz, 2025. gaia 2025 izango da eta 2024. gaia, -2020.
ABC triangeluan C erpinetik irteten den altueraren oina D da. Baldin AD = 2 cm, DB = 3 cm eta BC – CA = 0.5 cm badira, zenbat da triangeluaren perimetroa?
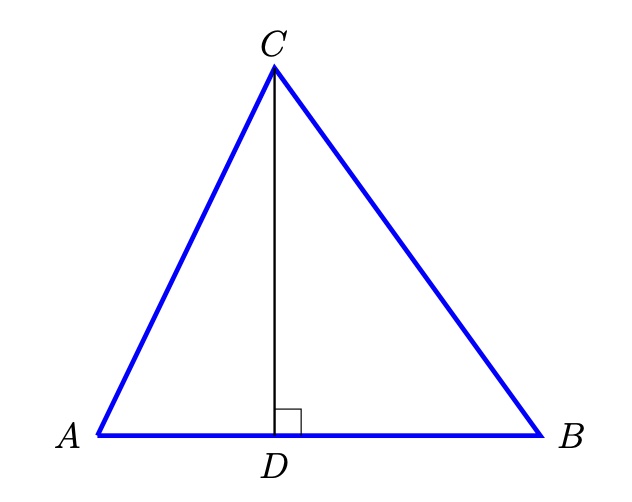
Ezkerreko eta eskuineko triangelu zuzenetan Pitagorasen teorema erabiliz,
AC2 = 22 + CD2 eta BC2 = 32 + CD2 .
Kendura eginez, BC2 – AC2 = 5. Hortik,
(BC + AC) (BC – AC) = 5,
eta BC – AC = 0.5 denez, BC + AC = 10 lortzen dugu. Perimetroa BC + AC + BA = 15 cm da.
Irudiko gelaxka zuriak pintatzeko hiru kolore ditugu: gorria, berdea eta urdina. Elkarren alboan dauden gelaxka bi, hau da, alde komun bat dutenak, kolore desberdinez pintatu behar dira. Zenbat modu ditugu lana egiteko?
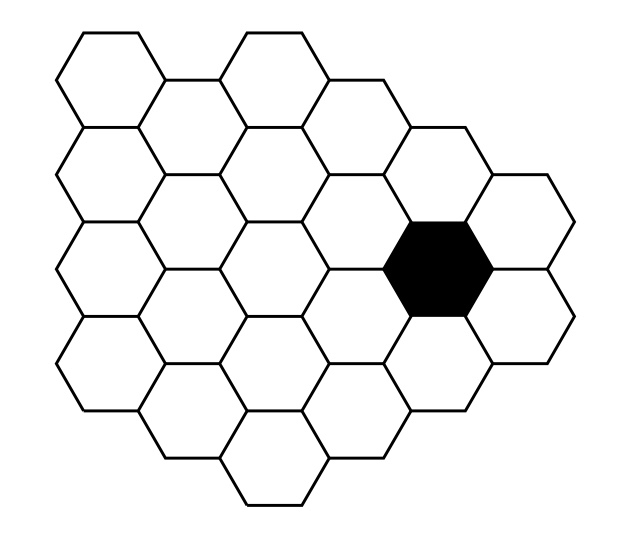
Goian ezkerrean dauden hiru gelaxkak kolore desberdinak dituzte, beheko irudian A, B eta C izendatu ditugunak. Behin hiru horiek finkatuta, beste guztiak derrigortuta daude, salbu eskuineko biak, D eta E izendatu ditugunak. Hor hiru aukera ditugu: D = A eta E = B; D = A eta E = C; D = C eta E = B.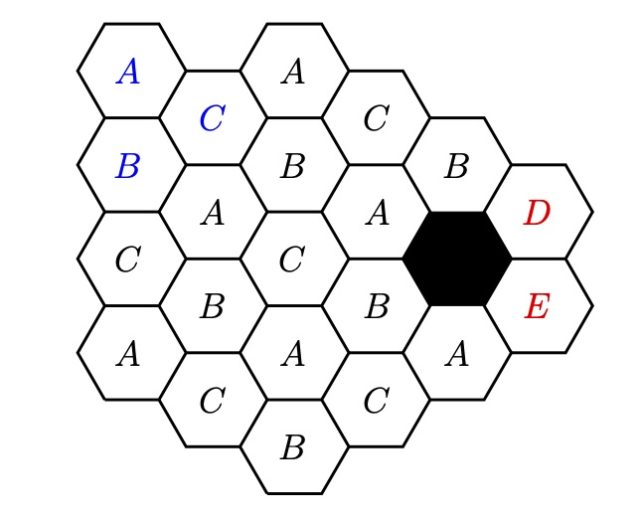
Hasierako hirurak pintatzeko sei modu daude, emandako koloreak permutatuz. Horietako bakoitzak hiru amaiera posible dituenez, 6 x 3 = 18 modu daude lana egiteko.
Urte arrunt batean, hau da, bisurtea ez den batean, bost igandeko bost hilabete egon dira. Asteko zer egun izan da Urteberri eguna? Gauza bera bisurte batean gertatu bada, zer egun izan da Urteberri eguna?
Urteberri eguna asteko egun bakoitzarekin probatuz, zenbat hilabetetan ageri diren bost igande ikustea izan daiteke ariketa egiteko modu bat. Ebazpide hori irakurleari utziko diogu eta hemen beste bat erakutsiko dugu.
Hilabete batek gutxienez lau igande eta gehienez bost ditu. Bost igandeko bost hilabete egon direnez, urte horrek 5 x 5 + 7 x 4 = 53 igande izan ditu. Urte arrunt batek 52 aste oso eta egun bat gehiago ditu (365 = 52 x 7 + 1), beraz, egun hori igandea izan da. Urteberri eguna kenduta 52 aste oso geratzen direnez, Urteberri eguna igandea izan da (baita Gabon zahar/Urtezahar eguna ere).
Bisurteak 52 aste oso eta egun bi dituenez, horietako bat igande izatea behar dugu, urtarrileko lehen bi egunetako bat, alegia. Orduan, Urteberri eguna larunbata edo igandea izan behar da.
Urtero daude bost igandeko lau hilabete gutxienez. Bosgarren bat egoteko, aipaturiko baldintza bete behar da.
Arrazoibideak asteko edozein egunetarako balio du, jakina. Aurten (2025) Urteberri eguna asteazkena izan denez, bost asteazkeneko bost hilabete ditugu. Bost igandeko bost hilabete izan zituen azken urtea 2023 izan zen eta hurrengoa 2028 izango da.
Egileaz:
Javier Duoandikoetxea Analisi Matematikoko Katedradun erretiratua da EHUn.