Kaosaz
Natura konplexua da. Natura ulertzen saiatzen diren zientzialariek, sarri asko, sinplifikatu eta biribildu egin behar izaten dute, fenomenoen arteko erregulartasunak aurkitu eta natura bera matematikoki deskribatu ahal izateko. XX. mendearen bukaeran, alor berri bat agertu zen fisikaren barruan, konplexutasun hori eta ekuazio ez-linealak aztertzeko xedearekin: kaosaren teoria.
Hainbat zientzialarik eta matematikarik ordurako heldu izan zieten bi gai horiei, batez ere Henri Poincaré frantziarrak. Hain zuzen, XIX. mende bukaeran ekuazio diferentzialen eta sistema dinamikoen teorian jardun zuen, eta 1908an hauxe adierazi zuen: sistema bateko hasierako baldintzen aldaera txikiek ezberdintasun handiak sor litzaketela sistema horren epe luzeko bilakaeran; adibide gisa eguraldia iragartzeko ezintasuna eman zuen. Alabaina, Poincaréren ideiek ez zuten berehalako arrakastarik izan, fisikari gehienak lanpetuta zebiltzalako ekuazio diferentzialak arrakastaz garatzen, teoria kuantiko eta erlatibista berriak ulertu nahian.
Kaosaren teoria ez zen benetan garatzen hasi meteorologian ordenagailuen erabilera ohiko bihurtu arte, II. Mundu Gerraren ostean. Izan ere, konputazioaren alorreko adituak orduantxe konturatu ziren meteorologiak planteatzen zituen arazoak (konplexuak eta ez-linealak, hain zuzen) proba-eremu bikaina izan zitezkeela, eta meteorologoek orduan ikusi baitzuten ordenagailuek izugarrizko aukera ematen zutela datu-kopuru oso handiak kudeatzeko eta eredu atmosferikoak eraikitzeko.
1961ean, Edward Lorenz eredu atmosferiko sinplifikatuen simulazioak egiten ari zen Massachusettseko Teknologia Institutuko ordenagailu batean. Une jakin batean, simulazioetako bat errepikatzea erabaki zuen, baina dena hasieratik egin ordez, erditik aurrera berrartzea erabaki zuen. Horretarako, ordenagailuak inprimatutako datuak erabili zituen. Gailuak kalkuluetarako sei dezimal hartzen zituen, baina hiru baino ez zituen inprimatzen; Lorenzek uste izan zuen milaren bakarreko desberdintasunak ez zuela ondoriorik izango emaitzan; bigarren simulazioan, ordea, guztiz bestelako emaitzak ikusi zituen. Hasieran, huts-hodiren batekin arazoren bat egongo zela pentsatu zuen, baina azkenean hasierako baldintzen aldaera txikien garrantzia onartu zuen.

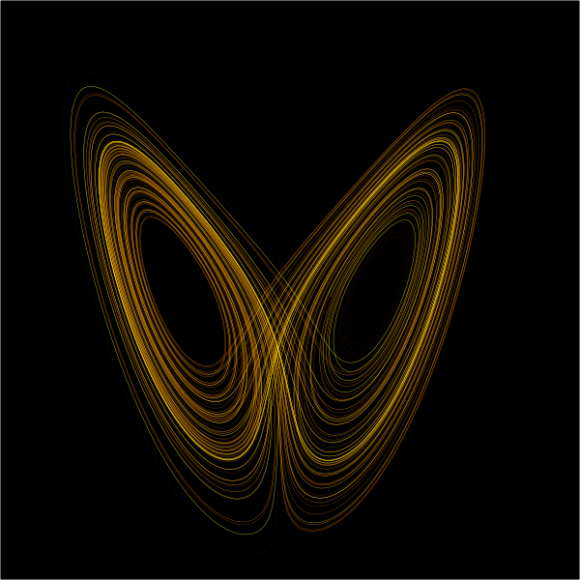
Lorenzek hasierako baldintzekiko sentikortasuna frogatu zuen (izen hori eman zitzaion fenomenoari), konbekzioaren eredua ezartzeko hiru ekuazio ez-linealeko sistema are sinpleago bat erabilita; eta, era berean, epe luzeko meteorologia-iragarpenak nahiko zentzugabeak liratekeela aurreratu zuen. Dena den, nolabaiteko ordena abstraktu bat ere erakutsi zuen emaitzetan agertzen zen jokaera nahaspilatu horren barruan: emaitzak hiru dimentsioko irudi grafiko bidez erakustean, kiribil bikoitz konplexu bat agertu zuen, zeina ez baitzen gurutzatzen edo errepikatzen, egitura eta muga zehatzak zituen arren. Irudia, ondoren «Lorenzen erakarlea» izena hartuko zuena, bere gainerako emaitzekin batera argitaratu zen 1963an, Deterministic nonperiodic flow izeneko artikulu batean. Izenburu hain deigarri hark determinismoak irauten zuela oihukatzen zuen, eta lana argitaratzeko aukeratu zuen aldizkariak, Journal of Atmospheric Sciences delakoak, bi datu adierazten ditu: batetik, Lorenzen arazoarekiko interesa nondik zetorren; bestetik, bere lana fisikari eta matematikarien sektore handi batentzat oharkabean igaroko zela.
Bien bitartean, Kaliforniako Unibertsitatean, Berkeleyn, Stephen Smale eta beste matematikari batzuk sistema dinamikoen ereduak egiteko moduak garatzen ari ziren, topologiaren bidez. Hau da: fase-diagrama batean puntu-multzoak tolestu edo luzatuz, sistema ez-linealetako joera iragarri ezinak erreproduzitzea. Hala, hasierako baldintzekiko sentikortasuna zehazten zuten; izan ere, tolestura-sekuentzia zein den kontuan hartuta, bi puntuk aukera dute edo elkarren oso urruti bukatzeko, edo elkarren oso hurbil.
70eko hamarkada hasieran, James Yorke matematikariak Lorenzen artikulua aurkitu zuen ustekabean eta horren berri laburra eskaini zuen matematika-aldizkari batean, Tien-Yien Li ikaslearekin batera, 1975ean: «kaos» terminoa erabili zuen tituluan (Period three implies chaos). Robert May izeneko fisikari-matematikariak, populazioen biologiako lanetan ziharduela, aurkitu zuen populazioetan aldaketa ziklikoak deskribatzen dituzten ekuazio ez-linealek, ausazkoak ziruditen fluktuazioak agertu baino lehen, periodoa bizkor bikoizten zutela; hala ere, itxurazko fluktuazio aleatorio horietan, ziklo egonkorrak agertzen ziren berriro, zeinak beste behin hasten ziren periodoak bikoizten, ausazkotasunerantz. Yorkek kaosaren teoria erabiliz azaldu zituen Mayren emaitzak. 1976an Mayk, Nature aldizkarian argitaratutako errebisio-artikulu baten bidez, kaosaren teoria hartzaile askoz gehiagorengana heltzeko aukera zabaldu zuen.
Sobietar matematikariak ere antzeko ikerketa-lerroak garatzen ibiliak ziren. Andrei Nikolaevitx Kolmogorov izan zen lehena 50eko hamarkadan, eta ondoren Oleksandr Mikolaiovitx Xarkovskii ukrainarrak jarraitu zion, zeinak Li eta Yorkeren ondorio berberak atera baitzituen; azkenik, Jakov Grigorievitx Sinai errusiarrak termodinamikaren arloan garatu zuen kaosaren teoria. Sobietar, mendebaldeko europar zein ipar amerikar, guztiak bat zetozen: kaosaren teoria modu egokia zen fluidoen mekanikan momentu hartara arte aurre egin ezin izan zitzaien arazoak lantzeko, batik bat turbulentziari eta faseen arteko trantsizioei zegozkienak.
Bestalde, Benoît Mandelbrot-ek eta beste matematikari batzuek, 70eko hamarkadan, adierazpide bisuala aurkitu zuten beren geometrian epe luzeko desordenaren barruko ordena periodikoarentzat. Mandelbrotek «fraktal» hitza sortu zuen forma irregularren mota berri bat deskribatzeko, zeinek, eskala eta dimentsio desberdinetatik behatuta, beren irregulartasuna bikoizten zutela baitzirudien.
Azkenik, 1976. urtean, Mitchell Feigenbaum matematikariak aurkikuntza garrantzitsua egin zuen, hain zuzen, konstante bakar batek deskribatzen zuela mailakatzea, hots, zikloak zein abiaduratan bikoizten ziren beren kaoserako bidean, edozein izanda ere sistema fisikoa edo funtzio matematikoa (koadratikoa nahiz trigonometrikoa).
Kaosaren teoria baliagarria izan zen oso: batetik, itxuraz konexiorik ez duten eta ustezko desordena jorratzen duten diziplinak batu zituen (besteak beste, biologia, ekologia, ekonomia, meteorologia edo fisika); eta, bestetik, konexio zuzena ezarri zuen matematika abstraktuen eta mundu errealeko arazoen artean.
Egileaz:
Cesár Tomé López (@EDocet) zientzia dibulgatzailea da eta Mapping Ignorance eta Cuaderno de Cultura Cientifica blogen editorea.
Itzulpena:
Lamia Filali-Mouncef Lazkano