Berriro gertatu zait. Telefono bat markatu dut eta beste aldeko ahotsak berehala salatu du zerbait oker egin dudala, ez zela hori markatu behar nuen zenbakia. Egiaztatzeko eskatu diot, ea zenbakia txarto hartuta ote nuen, baina ez, neurea izan da okerra: 5 sakatu behar nuen lekuan, 6 sakatu omen dut. Zergatik ez dute telefono-zenbakiek erroreak antzemateko koderik?

Aspalditik erabiltzen dira halako kodeak, ordenagailuaren ezinbesteko laguntzaz, zenbakien zuzentasuna ziurtatzeko. Bankuei ez zaie komeni bezeroen kontuen zenbakiak oker erabiltzea eta bati dagokiona beste bati ematea. Dendei ez zaie komeni salgai baten barra-kodearen zenbakia txarto tekleatu eta beste baten prezioa kobratzea. Ogasunari ez zaio komeni identifikazio-zenbaki okerra sartu eta zergak ordaindu behar dituenaren pista galtzea. Zenbakiak tekleatu behar ditugunean, noizean behin tekla okerra sakatzea hain arraroa ez denez, erroreak antzemateko bideak asmatu dira. Batzuk konplexu samarrak dira, beste batzuk sinpleak. Horren arabera, errore gehiago edo gutxiago antzemateko gauza dira.
Teknika sinple bat: hegazkin-txartelak
Hegazkin-txarteletan (eta zenbait bankutako txekeetan) oso metodo erraza erabiltzen zen: 4466820935 bazen txartelaren zenbakia, 4466820935-3 agertuko zen. Zergatik 3 hori? Zenbakiak 7rekin zatitzean uzten duen hondarra 3 delako (4466820935 = 638117276 x 7 + 3). Horrela, 6 tekleatu ordez 5 sakatuz gero, amaierako 3 horrek salatuko zuen zerbait txarto egin dugula. Era berean salatuko zuen 68 bikotearen ordez 86 emanez gero. Aldiz, ez zuen antzemango errorerik 0ren ordez 7 ipiniz gero, baina arraroa izango litzateke horrelako oker bat egitea, ezta?

Identifikazio fiskalaren letra
Duela 25 urte Espainiako Ogasunak erabaki zuen identifikazio agiriak zuen zenbakiari erroreak antzemateko kontrol bat jartzea. Aurrekoaren moduko oinarria duen metodoa da, baina aldatua: zenbakia 23rekin zatitzean lortzen den hondarra erabiltzen du. Orain 23 hondar posible ditugunez, 0tik 22ra, horietako bakoitzari letra bat esleitu zioten, taulak erakusten duen moduan.
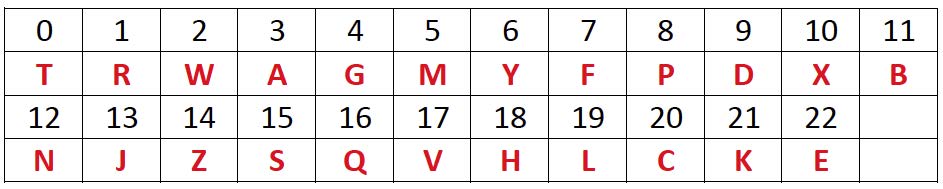
Esate baterako, 98765432 = 4294149 x 23 + 5 denez, eta taulan 5 hondarrari M letra dagokionez, 98765432M izango da identifikazio fiskaleko zenbakia. Hortaz, zenbakia tekleatu behar duen eskuak 98756432M idatziko balu, 5 eta 6 elkarrekin trukatuz, ordenagailuak ez lioke onartuko, 98756432 zenbakiak K letra eskatzen duelako, ez M.
Aurreko metodoaren ia antzekoa den arren, 23 aukeratzeak errore gehiago antzemateko balio du; esate baterako, digitu bat txarto badago edo ondoz ondoko digitu bi elkarren artean trukatu badira, metodoak beti adieraziko du errorea dagoela.
Salgaien barra-kodea
Erosten ditugun produktuek identifikazio-zenbaki bat dute. Irakurgailu automatikoen irakurketa errazteko barra-kode modura agertzen den arren, barra horiek zenbaki bat adierazten dute. Identifikazio horren bidez, berehala jakiten dugu produktua zein den. Irakurgailu automatikoaren ordez, zenbaki hori tekleatu ere egin daiteke eta, jakina, ez da errorerik egin behar erosi nahi dugun hori kobratu behar badigute eta ez beste zerbait. Horregatik, erroreak antzemateko kontrola du horrek ere.

Ohiko identifikazioa 13 digituko zenbaki batekin egiten da (EAN sistema, European Article Number). Lehen digitua aparte idazten da eta gero seiko multzo bi:
a0– a1 a2 a3 a4 a5 a6 – a7 a8 a9 a10 a11 a12.
Zerrendako azkena, a12, da kontrolerako erabiltzen den digitua. Honela kalkulatzen da: egin
S1 = a0 + a2 + a4 + a6 + a8 + a10 eta S2 = a1 + a3 + a5 + a7 + a9 + a11,
eta batu lehenengoa eta bigarrenaren hirukoitza, hau da, lortu S1 + 3 S2. Zenbaki horri gehitu behar zaiona 10en multiplo izateko, hots, azken zifra 0 izateko, hori da a12.
Liburuen ISBN (International Standard Book Number) identifikazio-zenbakiek ere EAN sistema erabiltzen dute [1]. Mahai gainean dudan liburu baten ISBN zenbakia 9788498608816 da. Egiazta dezagun ondo emanda dagoela:
(9+8+4+8+0+8) + 3 (7+8+9+6+8+1) = 154
denez, 6 batu behar diogu 160ra heltzeko. Hortaz, hamahirugarren digitua 6 izan behar da, hala denez.

Erroreak antzemateko, badaude horiek baino sofistikatuagoak diren bideak, hala nola bankuko kontuetarako edo kreditu-txarteletarako erabiltzen direnak. Baina telefono-konpainiek ez digute ezta kontrolik errazena eskaini oraindik eta dei okerrak egiten jarraituko dugu. Ondo pentsatuta, zertarako ekidin behar ditu konpainiak dei okerrak? Horiek ere fakturatzen dizkigu eta…
Oharra
[1] 2007an hasi ziren 13 zifrako EAN sistema erabiltzen liburuen ISBNrako. Horren aurretik 10 digituko ISBNak erabiltzen ziren eta kontroleko digitua, beste formula batek emanda, 0-tik 10eraino joan zitekeen. Baldin 10 egokitzen bazen, X idazten zen.
Egileaz: Javier Duoandikoetxea Analisi Matematikoko Katedraduna da UPV/EHUn.
1 iruzkina
[…] Y es que errar es de humanos. El matemático Javier Duoandikoetxea nos pone un ejemplo muy común: ¿quién no se ha equivocado al teclear un número de teléfono? Seguro que muchas y muchos de los aquí presentes. Pues aunque […]