Pitagorasen teorema kolokan? Bai zera!

Javier Duoandikoetxea

Pitagoras entzun eta teorema etorriko zaio akordura ia mundu guztiari. Hain ezaguna izan arren, Zientzia Kaiera honetan Pitagorasen teorema aipatu behar izan nuenez, Googlera jo nuen euskarazko esteka baten bila. Eman zidan lehen aukera egokia iruditu zitzaidan. Baina, begiak pantailan beherantza eramanda, deigarri egin zitzaidan zerbait ikusi nuen: Pitagorasen teorema gai modura zuen eta ETBk eman behar zuen dokumental baten berri. Bertan sakatu eta irudian ikus dezakezuen horrekin egin nuen topo. Harri eta zur geratu nintzen azpititulua irakurrita: Pitagorasen teorema kolokan!

Harritu eta larritu ninduena ez zen Pitagorasen teorema kolokan egotea, ondo baitakit hori ezinezkoa dela. Harrigarria da kolokan egon daitekeenik pentsatzen duenik egotea. Notizia zaharra zen eta ez dut dokumentala ikusteko aukerarik izan jakiteko zer den bertan gordetzen dena. Irakurtzen jarraitu eta hau ikusi nuen: “Izan ere, 2000 urtez Pitagorasen teorema zibilizazioarekin batera joan da aurrera eta gaur egun, Pitagorasek sortutako espazioa zalantzan jartzen hasi dira adituak. Dokumentalean lurra neurtzen jarriko dira, neurketa tresnarik aurreratuenak erabiliz, Pitagorasen teorema proban jartzeko, eta bere legea betetzen den ala ez egiaztatzeko”. Lehen esaldia agian hobeto ulertzen da gaztelaniazko bertsioan: “Dicho teorema ha ido evolucionando a lo largo de los últimos 2000 años”. Zer demontre da eboluzionatu duena?

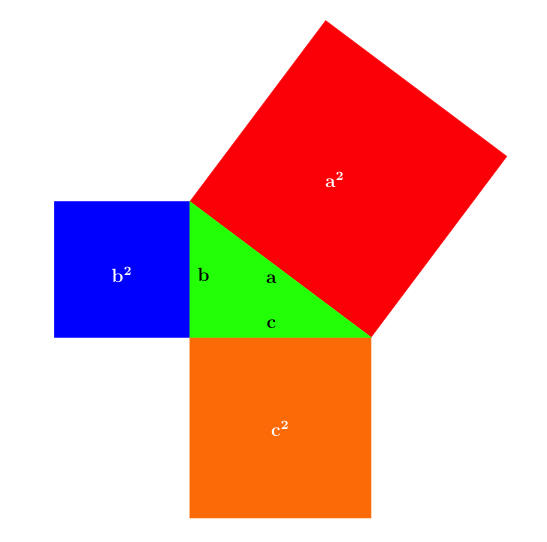
Hasteko Pitagorasen teoremak zer dioen aipatuko dugu. Triangelu batek angelu zuzen bat duenean, triangelu zuzena deritzogu. Horrelako triangelu batean alde luzeena hipotenusa da eta beste biak katetoak. Triangeluaren alde bakoitzarekin karratu bat eraikiz, hipotenusaren gaineko karratuaren azalera katetoen gaineko bien batura da. Ikurrak erabiliz eta a izanik hipotenusaren luzera eta b eta c katetoenak, hau betetzen da: a² = b² + c².

Pitagoras Egeoko Samos uhartean jaio zen K.a. VI. mendean eta Italiako Crotonan eskola filosofiko-erlijioso bat sortu zuen geroago. Haren jarraitzaileentzat ezaguna zen triangelu zuzenen propietate hori. Adituek diote lehenagotik ere ezaguna zela, babiloniarren artean esate baterako. Kontu zaharrak beraz…

Zergatik dakigu Pitagorasen teorema egiazkoa dela? Hurrengo irudiari begiratu eta berehala ikusten da. Eta beste modu asko daude frogatzeko.

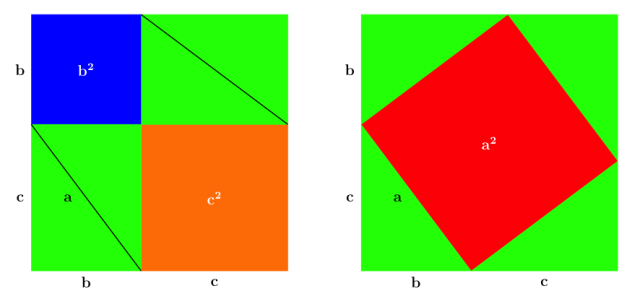
Hor triangelu baterako ikusi dugun frogak, ez digu beste baterako huts egingo? Matematikaren indarra da egia unibertsalak sortzeko gaitasuna. Berehala ulertzen da erabili dugun arrazoibideak beste edozein triangelu zuzenetarako ere balio duela. Ez dago bada hori kolokan jartzerik, ez orain ez gero.

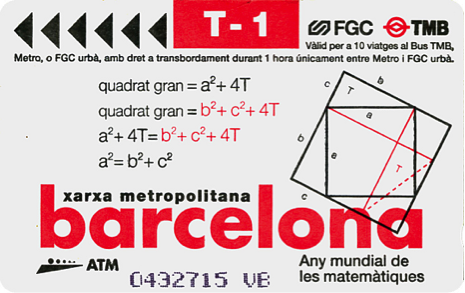
Hala ere, argi geratu behar da matematikaren objektuak abstraktuak direla. Matematikako “egiak” (teoremak) objektu ideal horiei buruzkoak dira beti. Teorema frogatuta dago arrazoibide logiko batek hipotesietatik ondorioetara eramaten bagaitu. Pitagorasen teorema planoko geometria euklidearreko hipotesietan kokatu behar da eta triangelu zuzenetarako balio du.

Eugene Wigner fisikariak artikulu ospetsu batean adierazten zuen moduan, harrigarria da abstrakzio hori zelan egokitzen den (dugun?) errealitatera eta zer-nolako ondorio praktikoak ateratzen ditugun hortik. Baina teorema matematikoen frogak ez daude mundu fisikoan. Itzul gaitezen bada Pitagorasen teoremara. Orduan, nik eraikitzen dudan triangelu batean ez bada Pitagorasen teoremak dioena gertatzen, zer? Bada, edo triangelua ez dago plano batean, edo ez du angelu zuzenik, edo neurriak txarto hartuta daude. Horiek jarri behar dira kolokan, eta ez teorema.

Planoko triangelu guztiek —eta ez zuzenek bakarrik—propietate hau dute: hiru angeluen batura 180^o da. Diotenez, Carl Friedrich Gauss matematikari bikainak propietate horretan oinarritutako esperimentu bat egin zuen: triangelu handi bat eraiki, angeluen batura egin eta ikusi ea emaitza 180^o zen. Triangelu handi hori egiteko hiru mendi tontor aukeratu zituen, bakoitzetik beste biak ikusteko moduko tontorrak, eta argi-izpiak bidalita osatu zuen triangelua. Erpin bakoitzean argi-izpien arteko angelua neurtu besterik ez zuen behar. Lortu zuen emaitza oso hurbil zegoen 180^o-tik, hain hurbil non aldea neurketaren errore posibleen azpitik baitzegoen. Hala ere, neurketaren erroreak kontuan hartuta, argi geratuko bazitzaion batura ez zela 180^o-koa, zer ondorio aterako zuen Gaussek? Triangelu baten angeluen batura 180^o dela dioen teoremaren faltsutasuna? Ez, noski, argi baitago teorema hori ondo frogatuta dagoela planoko geometria euklidearrean. Ondorioa izango zen triangelua ez zegoela plano batean, edo bestela esanda, munduko geometria ez zela euklidearra[1].

Aspalditik dakigu geometria euklidearra ez dela geometria bakarra. Aurten 100 urte betetzen dituen erlatibitatearen teoria orokorra formulatzeko, Einsteinek geometria riemanniarra erabili behar izan zuen. Hor ez dira betetzen geometria euklidearraren propietateak, baina abiapuntuko hipotesiak desberdinak izanik, ondorioak ere desberdinak izan daitezke. Ez dago kontraesanik horretan.

Bego argi bada, DBHko lehen mailako liburuetan gure gazteek aurkitzen duten Pitagorasen teorema hori ez dagoela kolokan jartzerik, zorionez.

Oharrak

[1] Batzuek zalantzan jartzen dute Gaussen esperimentuaren helburua eta uste dute haren asmoa ez zela geometria euklidearraren egokitasuna aztertzea.

Egileaz: Javier Duoandikoetxea Analisi Matematikoko Katedraduna da UPV/EHUn.