Udako ariketak amaitu ziren eta hemen datoz erantzunak. Soluzio bila aritu zaretenoi, buruari eragin diozuenoi, gure eskerrak ahaleginagatik. Emaitza zuzena lortu baduzue, zorionak! Eta, Zientzia Kaieran zuen ahaleginen ondorioa erakutsi diguzuenoi, erantzunak bidaliz, esker bereziak.
1) Zenbat gozoki ditu Anak?
Anak gozokiak ditu poltsa batean. Gozoki kopurua bi zifrako zenbaki bat da. Anak zifra horien batura egin eta horrenbeste gozoki ateratzen ditu poltsatik. Behin eta berriro egiten du gauza bera, poltsako gozoki kopurua zifra batekoa izan arte. Zenbat geratu zaizkio poltsan une horretan?
Azkenean 9 geratu zaizkio. Lehenengo urratsean 9ren multiploa geratuko zaio (Ramón San Juanek bidalitako erantzunean ikus dezakezue zergatik) eta hortik aurrera beti 9naka kenduko ditu.
Erraza iruditu bazaizue, segi pentsatzen: zein izango zen erantzuna 2015 gozokirekin hasita? Eta 16748rekin?
2) Zein da nire telefono zenbakia?
Nire telefono zenbakia ABCDEFGHIJ da. Letra bakoitza zifra desberdin bat da eta hau betetzen da: A>B>C, D>E>F et G>H>I>J. Gainera, D,E,F ondoz ondoko zenbaki bikoitiak dira, G,H,I,J ondoz ondoko zenbaki bakoitiak dira eta A+B+C=9. Zenbat da A?
A=8 da. A, B eta C-ren artean ezin da 9 egon, A+B+C=9 izan dadin. Hortaz, GHIJ=9753 da. Orduan, 1 izango da A, B edo C eta beste bien batura 8 izango da. Hori gertatzeko, DEF=642 da aukera bakarra. Telefono zenbakia 8106429753 da. Gure erabiltzaileek zuzen erantzun dute.
3) Zenbat da zenbaki guztien batura?
Bederatzi zenbaki txikitik handira daude idatzita. Erdikoa bederatzi zenbakien batezbestekoa da. Bost handienen batezbestekoa 80 da eta bost txikienena 50. Zenbat da zenbaki guztien batura?
Zenbakien batura 585 da. Idatz ditzagun ABCDEFGHI bederatzi zenbaki horiek. Hau esaten digute:
A+B+C+D+E+F+G+H+I=9E,
E+F+G+H+I=5 x 80=400,
A+B+C+D+E=5 x 50=250.
Azken biak batuta eta lehenengoa kontuan hartuta, E=65 da.
Joseluren erantzuna izan da zuzen heldu den bakarra eta berak oso modu dotorean lortu du E-ren balioa.
4) Zenbat langilek dakite euskara eta ingelesa?
Enpresa bateko 100 langileek euskara edo ingelesa hitz egiten dute. Ingelesa egiten dutenen artean, %37,5ek euskaraz ere badaki. Euskaraz egiten dutenen artean, %60a da ingelesez dakiena. Zenbat dira euskara eta ingelesa dakitenak?
Euskara eta ingelesa 30 langilek dakite. Joseluren erantzuna argi azalduta dago.
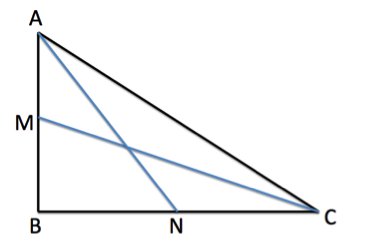
5) Zenbat da triangeluaren hipotenusa?
ABC triangelu zuzenak B erpinean du angelu zuzena. Izan bedi M AB aldearen erdiko puntua eta N BC aldearen erdiko puntua. Baldin AN=19 cm et MC=22 cm badira, zenbat neurtzen du triangeluaren hipotenusak?
Hipotesunaren luzera 26 da. Denbora luzez erantzun barik egon eta gero, azken orduan heldu zaigu ariketa honetarako erantzuna. Pitagorasen teoremak dio triangelu zuzen batean katetoen luzeren karratuen batura hipotenusaren luzeraren karratuaren berdina dela. ABC, ABN eta MBC triangelu zuzenak dira.
Idatz ditzagun AB=c, BC=a eta AC=b. Orduan, MB=c/2 eta BN=a/2. MBC eta ABN triangeluetan Pitagorasen teorema erabiliz,
a2+(c/2)2=222=484,
c2+(a/2)2=192=361.
Hortik, a2 eta c2 lor daitezke. Edo bestela, ekuazio biak batuta, 5(a2+c2)/4=361+484=845 da. Beraz, a2+c2=676. ABC triangeluan Pitagorasen teorema erabiliz, b2=676 eta b=26.
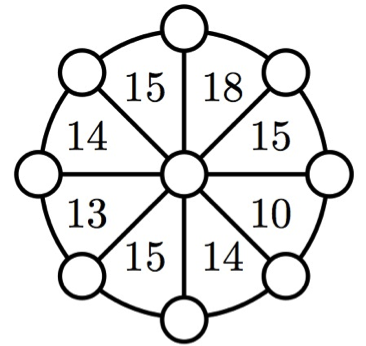
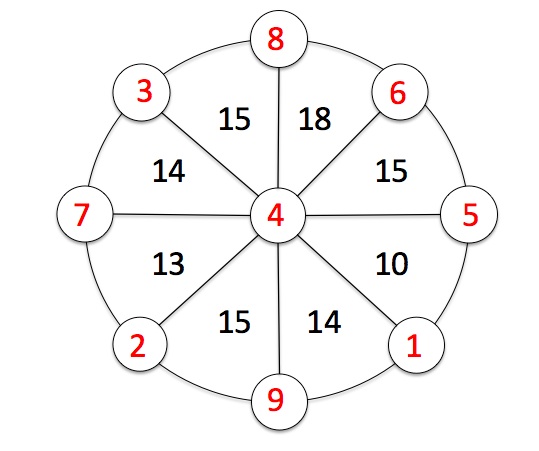
6) Hutsuneak bete
Kokatu 1etik 9rainoko zenbakiak irudiko zirkuluetan, triangelu bakoitzak dakarren zenbakia erpinetan dituen zirkuluetako zenbakien batura izan dadin.
Hau da erantzuna:
Zenbakiekin probatuz egin daiteke, lortu arte. Baina bide zuzen bat nahi izanez gero, hona hemen hau. Idatzita eman dizkiguten zenbaki guztien batura eginez, 114 lortuko dugu. Batura horretan erdiko zenbakia 8 bider kontatu dugu eta kanpoko bakoitza bi bider. Bestela esanda, 1etik 9rainoko zenbaki guztiak bi bider eta gainera erdikoa beste sei bider gehiago. Erdikoari E deituz,
114= 2(1+2+3+4+5+6+7+8+9)+6E.
Orduan, E=4 da. Hori jakinik ez da zaila besteak betetzea. Errazena 10 batura erakusten duen triangeluarekin hastea da.
Kasu honetan ere, izan ditugu erantzunak eta azkena izan da zuzena.
Eskerrik asko parte-hartzaile guztioi eta segi buruari eragiten, onuragarria baita!
Egileaz: Javier Duoandikoetxea Analisi Matematikoko Katedraduna da UPV/EHUn.