Hautatze-sistema ere hautatu behar da

Javier Duoandikoetxea

Hautagaiak, hautesleak, bozkak, emaitzak: ohituta gaude hauteskundeetara, izan politikoak edo bestelakoak. Gutxitan pentsatzen dugu, hala ere, hauteskunde prozesuaren aurretik hautu bat egin dela: zein izango den hautatze-sistema.

Hauteskunde batzuetan —esate baterako Espainiako hauteskunde politikoetan— zerrendei ematen zaie botoa eta, lortutako botoen arabera, zerrenda bakoitzari ordezkari kopuru bat esleitzen zaio. Beste batzuetan, botoa pertsonari ematen zaio eta bat bakarra da irabazlea. Herrialde batzuetan horrela aukeratzen dute estatuburua —adibidez Frantziako presidentea— eta ohikoa da hala egitea erakunde baten burua izendatzeko. Hauxe izango da hemen aipatuko dudan hauteskunde eredua. Hasteko, adibide batek erakutsiko digu hauteskunde-sistemaren garrantzia.

Adibide bat

Elkarte bateko presidente izateko bost hautagai aurkeztu dira: A, B, C, D eta E. Denetara 55 hautesle daude eta haien botoekin aukeratu behar da irabazlea. Hurrengo taulak biltzen ditu hautesleen lehentasunak [1]:

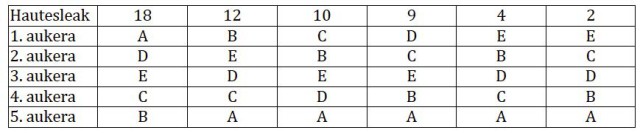Lehen zutabeak adierazten du 18 hauteslerentzat A dela aukerarik onena, A-ren ostean D dela gustukoena, E hurrengoa, C laugarrena eta B azkena. Horrela irakurri behar dira taularen zutabeak.

Ikus ditzagun zenbait hautatze-sistema eta kasu bakoitzeko irabazlea nor den

• Gehiengo erlatiboa. Botazio bakarra egiten da eta A hautagaiak beste edozeinek baino boto gehiago ditu: A da irabazlea.
• Bigarren itzulia lehen biekin. Lehen botazioan boto gehien dituzten biak bigarren itzulira pasatzen dira. Bigarren botazioan A-rentzat 18 boto dira eta B-rentzat 37: B da irabazlea.
• Azkena baztertu, bakarra utzi arte. Lehen botazioan boto gutxien lortu dituen hautagaia kenduta, beste botazio bat egiten da geratzen direnekin. Berriro azkena kendu eta horrela jarraitu behar da irabazlea lortu arte. Lehenengoan E baztertzen da, gero D, B eta A, ordena horretan: C da irabazlea.
• Borda metodoa. Hautesle bakoitzak hautagaiak ordenatu egiten ditu eta bere zerrendako lehenengoari 5 puntu ematen zaizkio, bigarrenari 4, hirugarrenari 3, laugarrenari 2 eta bosgarrenari 1. Puntuazio handiena D hautagaiak lortzen du: D da irabazlea.
• Condorcet metodoa [2]. Bikote posible guztiak egin hautagaien artean eta buruz buruko lehiak antolatzen dira. Hautagai batek buruz buruko guztiak irabazten baditu, hori da hautatua. Gure kasuan E beste edozeinen aurka ipinita, beti geratzen da aurretik: E da irabazlea.

Zein da ondorioa? Bistan da hautatze-sistemak erabateko eragina izan dezakeela emaitzan. Aztertu dugun adibidean, bost prozedura erakutsi ditugu eta zein erabili, irabazlea aldatu egiten da. Bada, beraz, zer erabaki botazioa egin aurretik. Gainera, kontuan hartu behar da hautesle kopurua (edo hautagai kopurua) oso handia bada, ia ezinezkoa izango dela sistema batzuk bideratzea.

Oharra: Hauteskunde estiloan aurkeztu dudan arren, zenbait aukeraren gaineko ordena jartzea beste egoera batzuetan ere gertatzen da. Aurreko A, B, C, D eta E horiek udal batek herrian egin nahi dituen lanak izan daitezke. Denak batera abiatu ezinda, jendeari galdetu nahi diote eta horren arabera ordenatu. Biztanle bakoitzak bere ordena badu ere, zelan hautatu “herri borondatea” erakutsiko duen zerrenda? Hor ez da bakarrik lehen postua erabaki behar, denak ordenatu behar dira.

Arrowen ezintasun teorema

Kenneth Arrow (New York, 1921) ekonomialaria da eta 1972ko Ekonomiako Nobel saria eman zioten; bera da orain arteko sariturik gazteena alor horretan. Nobel saria emateko arrazoien artean erabaki sozialei buruzko haren lana aipatzen da, besteak beste. Gizarte-zientzietan eta matematikan trebatua, teknika matematikoak erabili ditu beti gizarte arloko ikerketetan. Hona ekarriko duguna Social Choice and Individual Values izeneko doktore-tesian (Columbia University, 1951) agertzen da.

Arrowek aztertu nahi duen problema honela plantea dezakegu: talde bateko kide bakoitzak zenbait aukeraren artean lehentasuna finkatzen duenean, hau da, aukera horiek ordenatu egiten dituenean, aurkitu modu bat taldearen ordena finkatzeko. Bestela esanda, “herri-borondatea” adierazten duen zerrenda ordenatua lortu.

Arrowek baldintza batzuk jarri zizkion diseinatu nahi zuen hautatze-prozesuari

• Diktadorerik ez: hautesle bakar baten ordenak ez du taldearen ordena ematen.
• Paretoren baldintza: hautesle guztiek A aukera B-ren gainetik jartzen badute, taldearen ordenan A B-ren gainetik egongo da.
• Alternatiba hutsalekiko independentzia: A B-ren aurretik badago C aukera kontuan hartu barik, A B-ren aurretik dago, C aukera kontuan hartuta ere.
• Unibertsaltasuna: hautesleen lehentasunak edozein izanda ere, sistemak taldearen lehentasunak erabakitzeko modua izan behar du.

Zentzuzkoa dirudi baldintza horiek eskatzeak, ezta? Zer prozedura izango da egokia taldearen lehentasunak finkatzeko? Hau izan zen Arrowen erantzuna: hiru hautagai edo gehiago daudenean, ezinezkoa da aurreko propietate horiek guztiak aldi berean beteko dituen hautatze-sistemarik diseinatzea (Arrowen ezintasun teorema). Ondorioz, baliteke “herri-borondatea” ez egotea ondo definituta.

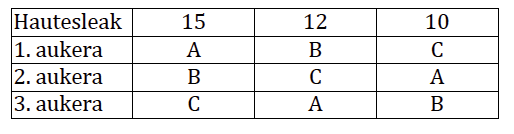
Intuizioak besterik iradokitzen digun arren, bada ordenazio indibidualetik kolektibora pasatzean gal daitekeen propietate bat: trantsitibotasuna. Eta horrek eragina du taldearen nahia definitzerakoan. Pertsona batek A aukera B-ren aurretik eta B aukera C-ren aurretik jartzen baditu, C baino A nahiago du. Hori da trantsitibotasuna. Taldean, ordea, baliteke ez gertatzea horrela. Ikus dezagun hurrengo taulako adibidea.

Taldearen desioetan A B-ren aurretik dago (25-12), B C-ren aurretik (27-10) eta C A-ren aurretik (22-15). Edozein delarik irabazlea, beti dago gehienek nahiago duten beste hautagai bat. Horri Condorceten paradoxa esaten zaio. Hain zuzen, lehenago aipatu dugun Condorcet metodoak ez luke irabazlerik emango kasu honetan.

Bistan da hautatze-sistema bat behar dela eta ez dagoela sistema idealik. Hortaz, horietako bat aukeratu behar da eta horren arabera jokatu. Orduan, behin sistema ezagututa, gerta daiteke hautesle batek edo gehiagok emaitzan eragin dezakeen estrategia bat prestatzea? Bai, baliteke, baina hori beste upel bateko sagardoa da.

Oharrak

[1] Adibide hau Las matemáticas en la vida cotidiana liburutik hartuta dago (L. A. Steen, ed., Addison-Wesley/Universidad Autónoma de Madrid, 1998).

[2] Borda sistema eta Condorcet sistema izenek gogora dakartzate sistema haiek proposatu zituzten Jean Charles de Borda (1733-1799) eta Nicolas de Condorcet (1743-1794) frantziarrak. Biak XVIII. mendekoak izanik, bistan da aspaldikoa dela hautatze-sistema on bat aurkitzeko interesa.

Egileaz: Javier Duoandikoetxea Analisi Matematikoko Katedraduna da UPV/EHUn.