Har bedi R erradioko behi bat

Josu Doncel

Matematika aplikatuan ari diren ikertzaileak hipotesiak aztertzen ibiltzen dira. Zertarako behar dituzte? Zergatik dira hain garrantzitsuak? Behi esferikoaren adibidea erabilita lortuko ditugu galdera hauen erantzunak.

Matematika aplikatuak sistema errealaren analisia du helburu. Ingeniaritza, fisika, kimika eta beste hainbat arlotan aplikatzen dira matematikak. Gainera, teknologia berrien agerpenarekin batera, sistema hauek gero eta konplexuagoak dira eta esan dezakegu matematikak ez direla atzean geratu, gaur egungo sistemen optimizazioan ere erabiltzen direlako.

Matematika aplikatuko lana hiru fasetan egiten da. Lehenengoan, sistema errealetik eredu matematiko bat sortzen da. Hori hipotesietan oinarritutako formulazioa eginez lortzen da. Bigarrenik, eredu matematikoa edukita, lan matematikoa egiten da, emaitza matematikoak lortzeko. Bukatzeko, emaitza matematikoak interpretatzen dira, sistema errealen portaera ulertzeko.

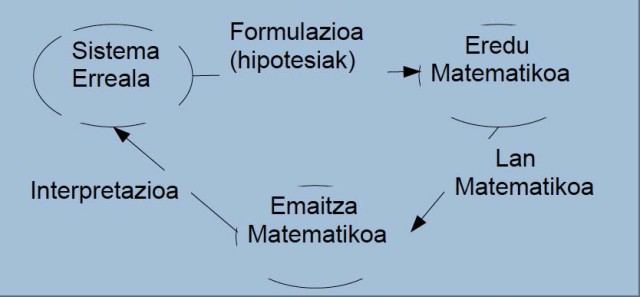
Matematika aplikatuan ari diren ikerlariek sistema errealak ondo definitzen dituzten eredu matematikoak bilatzen dituzte. Horretarako, hipotesi batzuk hartu behar dira gogoan eta, hori eginez gero, eredu oso konplexuak lortzen dituzte. Zoritxarrez, ezin da beti emaitza matematikorik lortu eredu matematiko konplexu horien bidez. Bestalde, beste hipotesi batzuk aztertuz gero, eredu bakunagoak lortzen dituzte, baino lortutako emaitzak oso urrun daude sistema errealetik.

Nekazari bati behiak gaixo jarri zitzaizkion behin. Beraz, haren behien analisia eskatu zuen matematikari talde bati. Ikertzaileek behin lana bukatutakoan txostena bat eman zioten nekazariari, egindako analisiak bertan bilduta. Txosten hori honela hasten zen: ‘Demagun R erradio duen behi bat…’

Esferak oso ezagunak diren elementu matematikoak dira eta, hori dela eta, behi bat R erradioko esfera bat dela onartuz gero, behi hori guztiz deskribatu ahal da. Argi dago behi bat ez dela esfera bat. Baino, nekazariak duen behi kopurua handia bada, oso lan zaila da ikerlarientzat behi bakoitzari analisia egitea eta lortutako emaitza guztiekin interpretazioa bat egitea.

Hipotesi egokia aukeraketa, orduan, garrantzi handikoa da matematika aplikatuetan ari diren ikertzaileentzat. Oinarrizko matematiketan, ordea, lan matematikoa garatzea da helburua eta sistema errealen formulaziorik ez da egiten. Beraz, hipotesiek garrantzi txikiagoa dute oinarrizko matematiketan. Hala ere, oso garrantzitsutzat jotzen dut oinarrizko matematiketan egiten den ikerketa, zientziako arlo askok oinarrizko matematikan garatzen den teoria erabiltzen dutelako.

Egileaz: Josu Doncel Matematikan doktorea da eta egun, INRIA Institutuan dihardu ikertzen.