Talboten efektua aurkeztu genuen “Talboten efektua (I): fenomeno bitxi baten jaiotza” artikuluan eta hura gertatzearen arrazoiak aztertzen hasi ginen. Hasteko, egoera zirrikitu bakarrera sinplifikatu genuen, eta uhinen difrakzioa eta Huygensen printzipioa erabiliz, zer gertatzen ari zen ulertzeko gai izan ginen.
Oraingoan, aurrera pausu bat emango dugu printzipio berekin Youngen esperimentua azalduz. Azkenik, Talboten fenomenoaren atzean dagoen fisika konplexua behatuta, Talboten alfonbra eratzearen arrazoiak ikusteko gai izango gara.
Youngen bi zirrikituen esperimentua
Esan bezala, beraz, suposa dezagun bi zirrikituko sareta dugula.
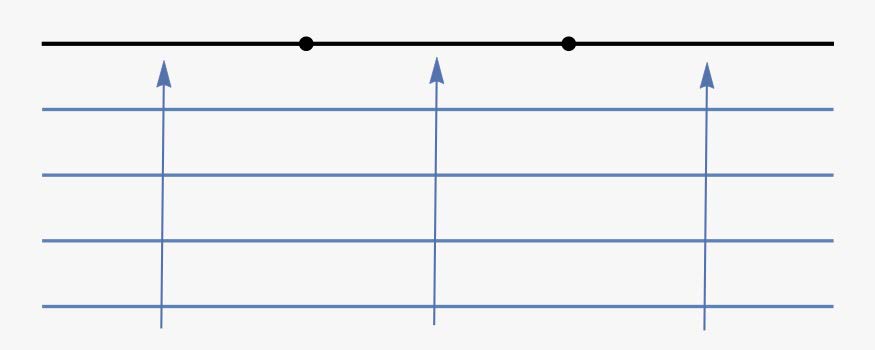
Zirrikitu bakarraren kasuari eta intuizioari jarraituz, pentsa genezake beste aldetik begiratuz gero zirrikitu parea argiztatuta ikusiko dugula, eta kito. Zer gerta liteke, bada, bestela?
Hori da, hori, fisikak intuizioari emandako zaplaztekoa. Zulo bakoitza bere aldetik hartuz beste aldetik zuloa argiztatuta ikusten badugu, biak batera aztertzean zergatik ez ditugu, besterik gabe, biak argiztatuta ikusten? Gu bezainbeste harrituko zen hasiera batean Thomas Young fisikari eta egiptologo britainiarra (Somerset, 1773 – Londres, 1829). Hau ere ez zen fisikan bakarrik aritu; Rosetta harria deszifratzeko aurrera pauso handiak egin zituen, Jean-François Champollion frantziarrak osorik deszifratu baino urte gutxi batzuk lehenago. Ur-uhinetan sortzen ziren interferentzia fenomeno berberak behatu zituen argiarekin esperimentatzean, eta beraz, interferentzia uhinen ezaugarria izanik, argiak uhina izan behar zuela ondorioztatu zuen. Gu aztertzen ari garen berbera izan zen, hain zuzen ere, Youngek egin zuen esperimentua, eta 1803an Royal Society izenekoan aurkeztu zuen. Bere omenez, Youngen bi zirrikituen esperimentua deitzen zaio.
Huygens ez litzateke horrenbeste harrituko 2. irudia ikustean. Izan ere, bere printzipioaren arabera, zulo bakoitzak uhin esferikoen iturri gisa jokatuko du eta aurreko artikuluan ikusi genuen 5. irudiko egoera sortuko da.
Irudi honek agerian uzten du uhinen arteko interferentzia deritzona. Leku batzuetan, uhin batek bestearekin bat egin eta uhin handiagoa sortuko dute: uhinak fasean daudela esaten da, eta interferentzia eraikitzailea gertatzen da. Bestalde, beste puntu batzuetan uhinek elkarrekin talka egiten dute eta elkar deuseztatzen dute: oraingoan uhinak guztiz desfasatuta daude eta interferentzia suntsitzailea gertatzen da.
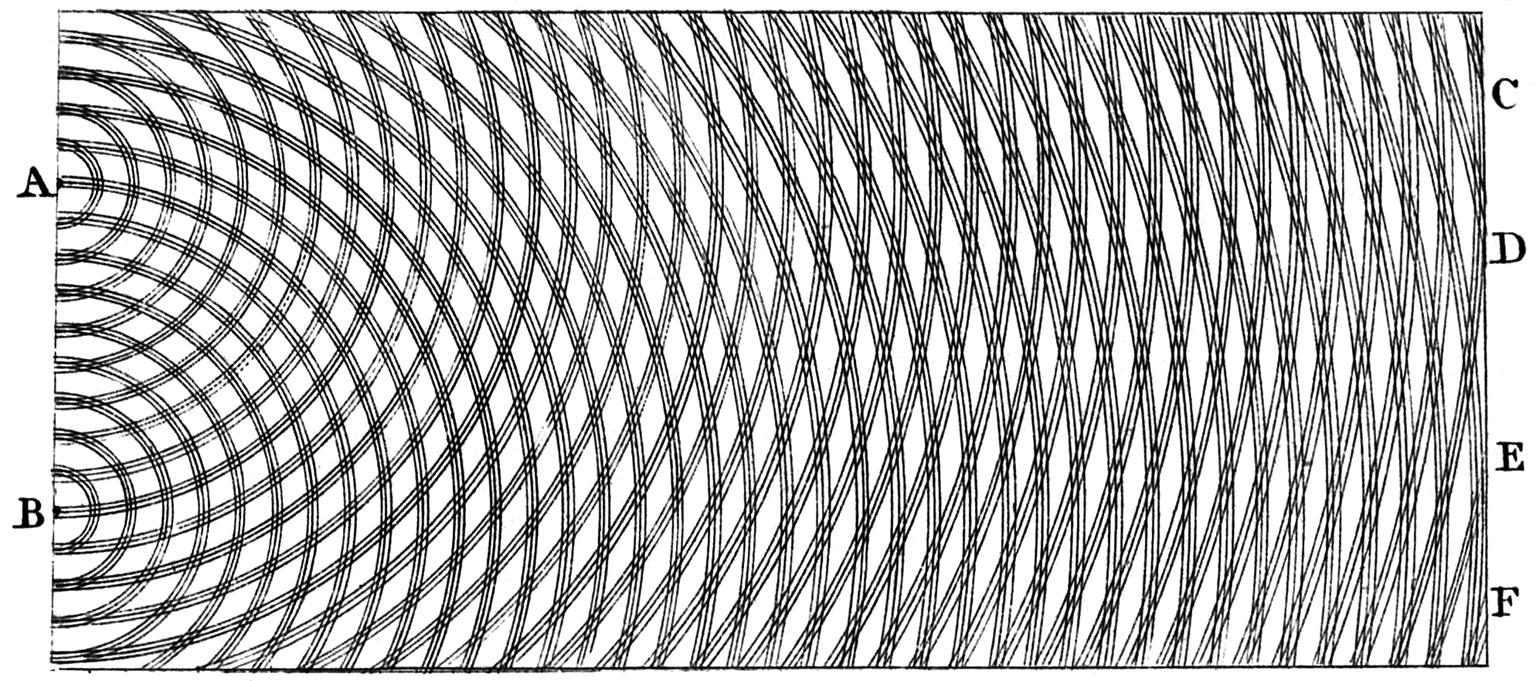
Youngen marrazkiaren eskuinaldean (4. irudia) nahiko argi ikusten dira zenbait marra zuzen, batzuk argiagoak eta besteak ilunagoak. Hain zuzen ere, horiek dira hurrenez hurren interferentzia eraikitzailea eta interferentzia suntsitzailea gertatzen diren puntuen adierazpena. 3. irudian, interferentzia eraikitzailekoak atzeman daitezke (urrutitik begiratuta, ikus al ditzakezu bi zuloen erdian sortzen diren lerro zuri batzuk?). Suntsitzailekoak, ordea, ez dira horren begi-bistakoak. Lana errazteko, denak 5. irudian adierazita daude.
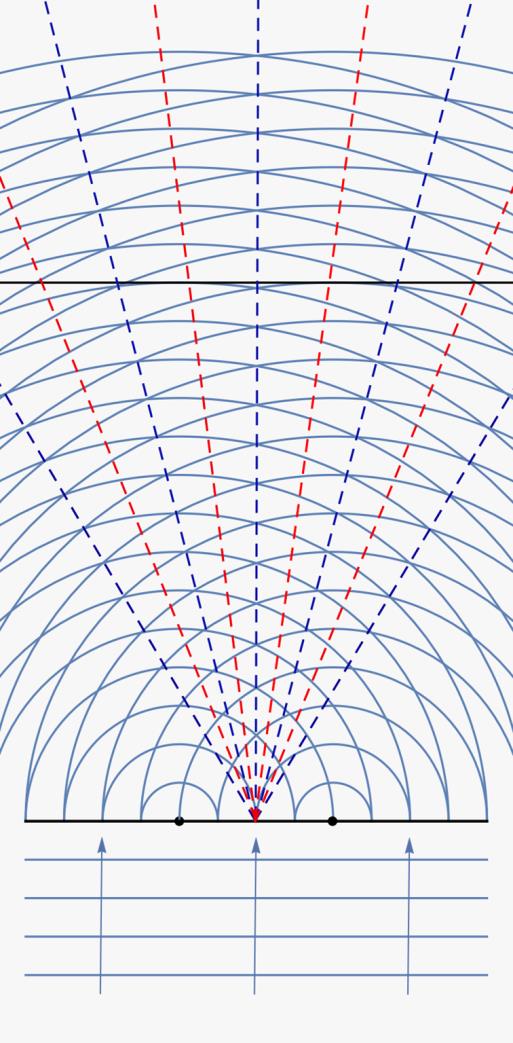
Begiratu marra beltzak adierazten duen pantaila. Marra urdinek mozten duten puntuan uhina indartsua da; marra gorriko puntuetan, berriz, ez da uhinik egongo. Hala, argi dago intermitentea den eredu bat islatuko duela, 2. irudian ikusten dena, hain zuzen ere.
Talboten efektua
Honaino iritsita, trebatu gara zirrikituen kontuak aztertzeari dagokionez. Horrela, aurreko artikuluaren 4. irudiko Talboten esperimentuan Youngi gertatutakoaren antzekoa gertatuko dela espero dugu. Huygensen printzipioa erabiliz, egoera zaildu egingo da zirrikitu kopuruarekin.
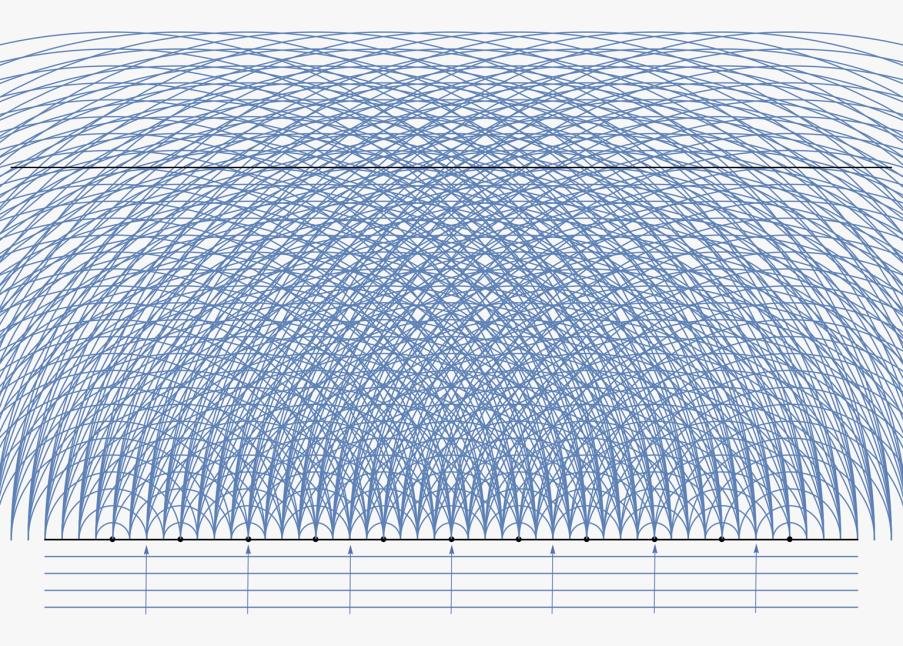
Problemaren ebazpen analitikoa ez da berehalakoa, eta uhinen eta Schrödingerren ekuazioekin egin behar da lan. Hemen, emaitzak besterik ez ditugu azalduko, askori hauen edertasunaz gozatzea nahikoa izango zaiolakoan.
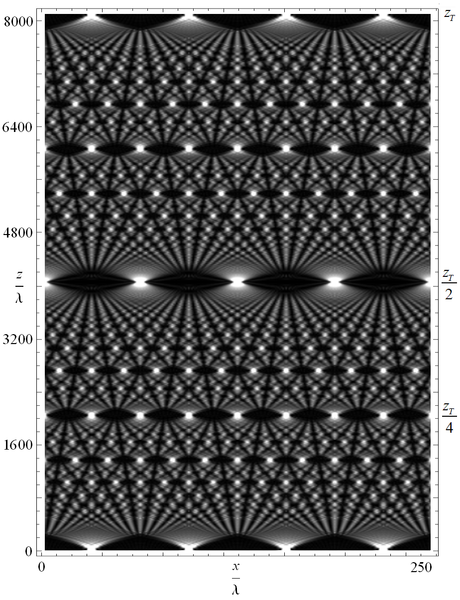
Horrela, bada, iritsi gara hasierako Talboten alfonbrara. Aurretik ikusitakoari esker, gai izango gara hura ondo ulertzeko. Izan ere, 6. irudiko ezarpen berbera dugu hemen: behealdeko puntu zuriak saretako zulo argiztatuak dira, eta argia behetik gora hedatzen da. Gune zuriek interferentzia eraikitzailearen ondorioz sortutako argia adierazten dute; beltzuneak, ordea, argirik ez dagoen tokiak dira.
Honela ulertu behar dugu irudia: aurreko irudietan kokatu dugun pantaila horizontal hori Talboten alfonbran kokatuko bagenu, orduan pantailak ebakitzen dituen gune zurietan bakarrik ikusiko genuke argia.
Adibidez, pantaila irudiaren goialdean jarriko bagenu, ikusiko genuke zirrikituen pareko lerroak bakarrik leudekeela argiztaturik. Hau nahiko harrigarria da; izan ere, Talboten esperimentuak irudian Z𝑇 izendatua izan den distantzian sareta erreproduzitzen du. Ez hori bakarrik, pantaila irudiaren erdian, ZT ⁄2 delakoan, kokatuko bagenu, trasladatutako sareta islatuko litzateke bertan. Eta laurden batean, saretaren kopia estuago bat izango genuke. Herenean, are estuagoa oraindik, eta zortzirenean are estuagoa.
Oro har, Z𝑇 distantziaren edozein frakziotan saretaren kopia bat lortuko dugu, eta frakzio hori 𝑝/𝑞 era laburtuan idazten badugu, 𝑞 aldiz estuagoa izango da (nahiz eta salbuespenak dauden, 𝑞 bikoitia bada orduan 𝑞/2 aldiz estuagoa izango da).
Z𝑇 distantziaren hurbilpen onak ezagutzen dira. Ziurrenik John William Strutt, Lord Rayleigh ingelesak (Essex, 1842 – Essex, 1919) egin zuen ekarpen garrantzitsuena, 1881n argitaratutako artikulu batean; bertan, argi monokromatikoarekin lanean arituz gero, alegia kolore bakarreko argiarekin eta ez argi zuriarekin arituz gero, orduan
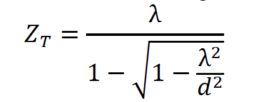frogatu zuen. Hemen λ argiaren uhin-luzera eta d zirrikituen arteko distantzia dira. Gainera, askotan uhin-luzera oso txikia da zirrikituen tartearekin konparatuta, eta kasu horretan 
adierazpenak hurbilpen on bat emango digu. Beraz, distantzia honen frakzio guztietan hasierako saretaren kopiak sortzen dira.
Estetika besterik ez?
Talboten alfonbrak polita bezain ustekabekoa den fenomeno fisiko bat irudikatzeko balio du besterik gabe. Baina fisikan eta matematikan (oro har, zientzian) gertatu ohi den bezalaxe, duela bi mendeko akademikoek ezagutzen zituzten arauei jarraituz lortutako zientzia-bitxikeriek industriako teknologia garrantzitsuetan aurkitu dute aplikazioa.
Horien artean aitzindaria Lord Rayleighen artikulua dugu; hantxe bertan baitio Talboten esperimentuari esker sareta oso estuen kopia zehatzak lor daitezkeela argiarekiko oso sentikorra den pantaila Z𝑇 distantzian ipiniz. Kopia horiek egitea ez zen lan erraza; izan ere, Rayleighek zentimetroko 6800 zirrikitu zituen sareta erabiltzen zuen…
Baina aplikaziorik emankorrenak XXI. mendekoak ditugu. Izan ere, Talbot effect application: Measurement of distance with a Fourier-transform method artikuluan erakusten dute Talboten efektua industriako neurketa zehatzak egiteko erabil litekeela. Horrekin lotuta dago litografia atomikoa deritzona. Teknika honetan, atomo izpi bat egitura lau baterantz bidaltzen da, eta hesi baten funtzioa betetzen duen uhin batek sortutako patroiari jarraituz, egitura nanometrikoak oso zehatz eraikitzen dira. Hainbat lanek proposatu dute Talboten efektua helburu honetarako erabiltzea; izan ere, tarte handiko sareta batean Z𝑇 kalkulatu eta bere 𝑝/𝑞 frakzioan pantaila ipini dezakegu hasierako sareta baino 𝑞 aldiz estuagoa den bat sortzeko. Nahikoa izango da 𝑞 oso handia hartzea sareta oso estua lortzeko, eta beraz, patroi nanometriko bat lortzeko.
Ezingo dugu jakin zer pentsatzen zuen Talbotek bere aurkikuntzari etorkizunean emango zitzaizkion erabilerei buruz. Agian pentsatuko zuen noizbait norbaitek emango ziola erabilera on bat, argazkigintzan agian, baina seguruenik ez zuen pentsatuko bi menderen buruan bere esperimentuak egitura nanometrikoak eraikitzeko balioko zuenik, ezta bere gela dekoratzeko alfonbra eder bat sortzeko balioko zuenik ere!
Erreferentzia bibliografikoak
- Young, Thomas, (1807). Course of Lectures on Natural Philosophy and the Mechanical Arts. London.
- Strutt, John William, (1881). On Copying Di raction-gratings, and on some Phenomena connected therewith. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 11, 195-205.
- Schirripa Spagnolo, G. & Ambrosini, D., (1999). Talbot effect application: measurement of distance with a Fourier-transform method. Measurement Science and Technology, 11 (1), 77-82. DOI: 10.1088/0957-0233/11/1/312
Egileaz: Daniel Eceizabarrena matematikaria da eta Basque Center for Applied Mathematics (BCAM) ikerketa-zentroko ikertzailea.