Konposizio metodoak ekuazio diferentzial arrunten (EDAen) sistemen hasierako baliodun problemen zenbakizko ebazpenerako algoritmoak eraikitzeko tresna ahaltsuak dira. Konposizio metodo bat oinarrizko zenbakizko metodo bat edo batzuk zenbaitetan konposatzearen emaitza da. Honela, s konposizio eginez lortzen den metodoari, s ataleko konposizio metodoa esaten zaio.
Oinarrizko integratzaile gisa bigarren ordenako metodo simetrikoa darabilten konposizio metodo simetrikoei erreparatuko diegu. Konposizio metodoa simetrikoa izateak esan nahi du oinarrizko integratzailea simetrikoki konposatu dela. Honelako prozesuen helburua izaten da, oinarrizko metodoaren zenbait propietate mantenduz zehaztasun ordena altuagoko metodoak lortzea.
Simetria baldintzek konposizio metodoaren ordena bikoitia izatea ziurtatzen dute. Bestalde, konposizio metodo simetrikoa zehaztu dugun ordenakoa izan dadin, beharrezkoa da atal kopuru minimo bat izatea. Adibidez, 8 ordenako konposizio metodoak gutxienez s=15 atal izan behar ditu, eta 10 ordenakoak, gutxienez s=31 atal. Asko dira konposizio metodoen koefizienteak bilatzen jardun duten autoreak. Honela, ezaguna da aipaturiko eran lortutako 8 ordenako metodorik onenak 17 atal dituela, eta 10 ordenako eta 31, 33 eta 35 ataleko metodo oso onak ere lortu direla.
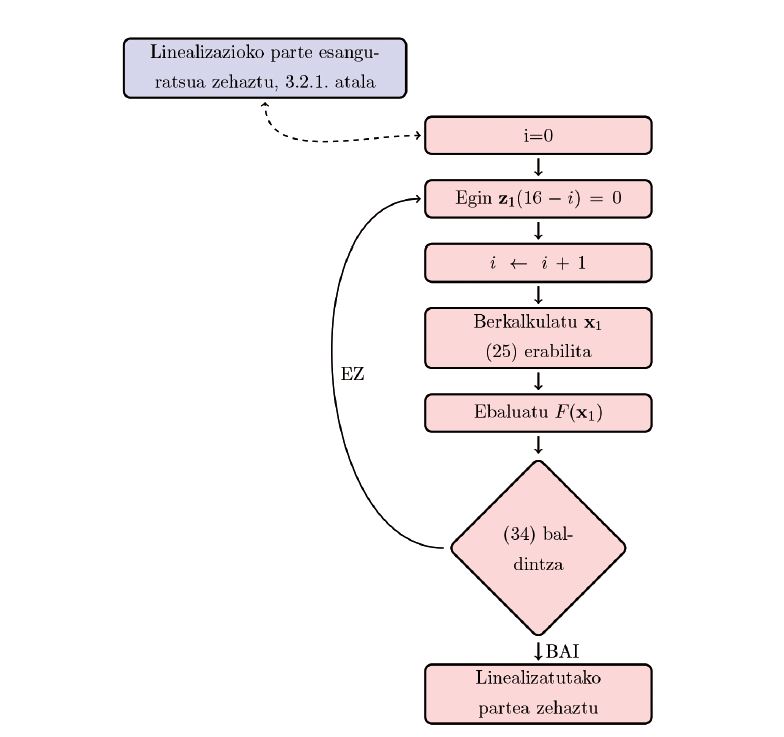
Lan honetan 10 ordenako eta 31 ataleko konposizio metodo simetrikoak lortzeko sortu ditugun bi teknika aurkezten dira. Atal kopuru minimoa duen konposizio metodoan, parametro kopurua eta murrizketa aljebraikoen kopurua bera da (10 ordenakoetan zehazki hamasei), eta Newton-en metodoa erabil daiteke soluzioak lortzeko, soluzioen hasierako hurbilpen egokiak izanez gero.
10 ordenako eta 31 ataleko metodo simetrikoen kasuan, milaka soluzio daude, eta horien artean, irizpideren baten arabera onena edo onenak hartzen dira. Hainbat autorek erabilitako irizpidea tarte osoan ibilitako distantzia minimizatzean datza eta guk ere irizpide horri jarraituko diogu. 10 ordenako eta 31 ataleko metodoen artean, Sofroniouk eta Spalettak proposatutakoa da egun ezagutzen den onena. 10 ordenako konposizio metodo simetrikoak hamasei ordena-baldintza bete behar ditu. Ordena-baldintzetako ekuazioak oso konplexuak dira, eta aipatutako autoreek, teknika eraginkor bat diseinatu beharrean, konputagailu ahaltsuen indarra erabili zuten beraien metodoa lortzeko.
Hemen, gure helburua izan da aipatutako metodoak sortzeko teknikak diseinatzea eta berauek probatzea. Sofroniouk eta Spalettak lortutako 10 ordenako eta 31 ataleko metodoa edota hobeak lortzea, guk diseinatutako teknikez baliatuz. Diseinatu ditugun teknika bietan, hamasei ordena-baldintzek osatzen duten sistemaren azpisistema bat ebatziz hasten dugu prozesua. Azpisistema hau 5 ekuaziok osatzen dute, eta ekuazio hauek betetzen dituzten emaitzen multzotik norma euklidearra lokalki minimizatzen duten puntuak aukeratzen ditugu. Ondoren, falta diren beste 11 ordena-baldintzak betearazteko bi bide proposatzen ditugu.
Teknika biak izan dira gai Sofroniouk eta Spalettak lortu zuten soluzioa lortzeko eta bigarren teknikak, beste soluzio batzuk ere eman dizkigu. Teknika hauek erabil daitezke ekuazio polinomikodun sistemak askatzeko (bereziki, ordena altuko zenbakizko integratzaileen sorreran ageri direnak askatzeko).
Artikuluaren fitxa
- Aldizkaria: Ekaia
- Zenbakia: Ekaia 34
- Artikuluaren izena: Integratzaile simetrikodun 10 ordenako konposizio metodo simetrikoen bilaketa.
- Laburpena: Konposizio metodoek, Ekuazio Diferentzial Arruntak (EDAak) ebazteko oinarrizko zenbakizko integrazio-metodo bat modu egokian konposatuz emaitzak hobetzeko aukera ematen dute. Lan honetan erreparatuko diegu bigarren ordenako zehaztasuna duen oinarrizko integratzaile simetriko bat erabiliz lortzen den konposizio metodo simetrikoei. Simetrien erabilerak, ordena-baldintzak sinplifikatzeaz gain, ezezagunen kopurua gutxitzea eragiten du. Asko dira honelako metodoen koefizienteak bilatzen jardun duten autoreak. Honela, ezaguna da aipaturiko eran lortutako 8 ordenako metodorik onenak 17 atal dituela, eta 10 ordenako eta 31, 33 eta 35 ataleko metodo oso onak ere lortu direla. Lan honetan 10 ordenako eta 31 ataleko konposizio metodo simetrikoak lortzeko sortu ditugun bi teknika aurkezten dira.
- Egileak: Elisabete Alberdi Celaya, Joseba Makazaga Odria, Ander Murua Uria.
- Argitaletxea: UPV/EHUko argitalpen zerbitzua.
- ISSN: 0214-9001
- Orrialdeak: 99-121
- DOI: 10.1387/ekaia.19341
Egileez
Elisabete Alberdi Celaya UPV/EHUko Bilboko Ingeniaritza eskolako Matematika Aplikatua Sailean dabil eta Joseba Makazaga Odria eta Ander Murua UPV/EHUko Informatika Fakultateko Konputazio Zientzia eta Adimen Artifiziala sailean.
Ekaia aldizkariarekin lankidetzan egindako atala.