Elur-maluta matematikoa

Javier Duoandikoetxea

Elur ugari ekarri zigun neguak Euskal Herrira eta halakoetan edonon agertzen diren paisaia zuritu ederrak erakutsi zizkiguten hedabideek. Baina begiekin ikusten ez den edertasuna ere badu elurrak, Zientzia Kaiera honetako Izotz-kristalen zientzia artikuluan Leire Sagronizek eta Ainara Sagronizek azaldu zigutenez. Matematikak ere badu bere “elur-maluta” (egokiago izango litzateke “izotz-kristala” deitzea), benetako horiek bezain polita. XX. mendearen hasieran asmatu zuen Helge von Koch matematikari suediarrak. Ez, ordea, benetako izotz-kristalen eredu modura, kurben propietate matematiko bati begira baizik.

Von Kochen kurba

Von Kochek proposaturiko kurba urratsez urrats eraikitzen da. Hasteko, hartu zuzenki bat. Ondoren, kendu zuzenkiari erdiko herena eta haren ordez luzera bereko zuzenki bi ipini, 60^o-ko angeluak osatuz (ikus 2. irudia). Beste moduz batez azalduta, erdiko herena oinarri hartuta egin triangelu aldeberdin bat; gero, oinarria kendu eta beste alde biak utzi. Jardunbide hau izango da oinarrizko prozesua.

Orain lau zuzenki ditugu eta bakoitzari oinarrizko prozesua egingo diogu. Horrela, zuzenki bakoitzaren lekuan haren luzeraren herena duten lau zuzenki agertuko dira. Bigarren urratsean, 16 zuzenki ditugu eta bakoitzarekin oinarrizko prozesua eginda, 64 zuzenkira pasatuko gara, eta abar. Ikus 3. irudian lehen urratsak.

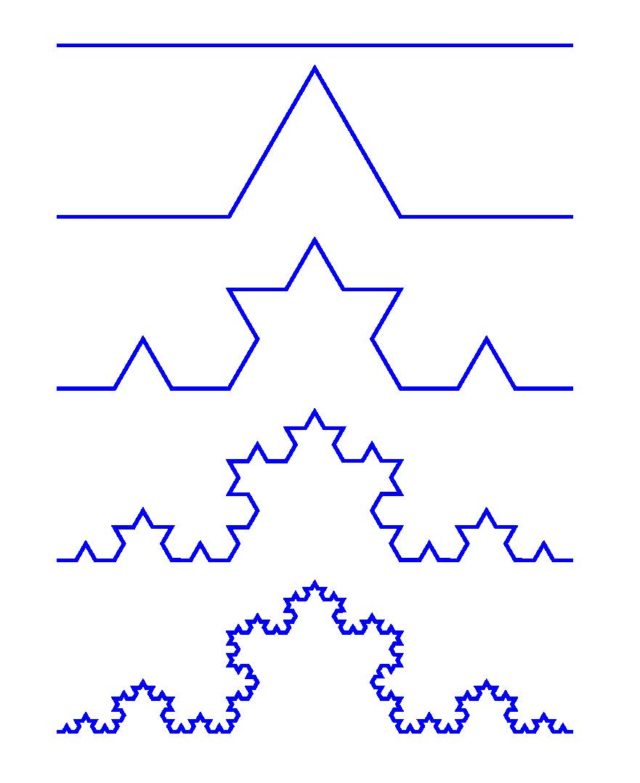
Behin eta berriro oinarrizko prozesua eginez, kurba-segida bat dugu eta limitean lortzen den kurba (“infinitu urrats” egin ondoren, alegia), horixe da von Kochen kurba.

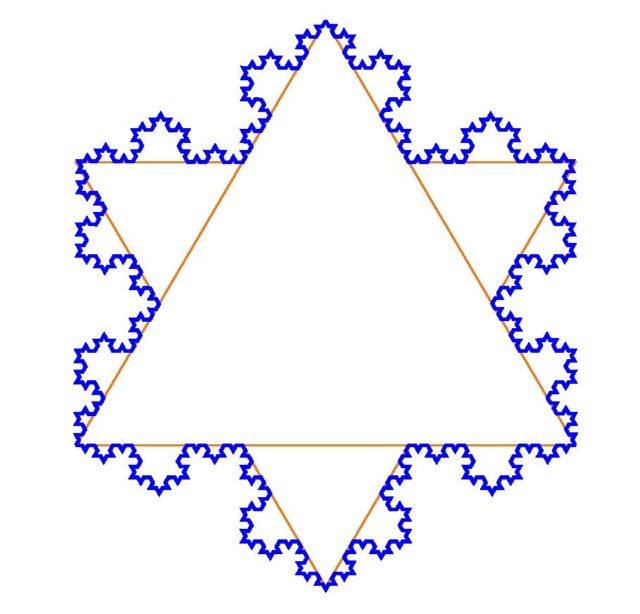
Non dago elur-maluta? Hasieran zuzenki bakarra erabili ordez, triangelu aldeberdin baten hiru aldeak erabiliz gero, lortzen den kurba itxiak simetria hexagonala du eta oso irregularra da. Nolabait izotz-kristal baten itxura duelako eman zioten “elur-maluta” izena. Ikus 4. irudia. Esan dezadan von Kochek bere artikuluan zuzenki bakarrarekin eraikitako kurba baino ez zuela proposatu, geroko irudia da elur-malutarena.

Testuinguru matematikoa

Zergatik asmatu zuen von Kochek kurba hori? Haren artikuluaren izenburuak azaltzen digu arrazoia: “ukitzailerik gabeko kurba jarraitu bat, oinarrizko eraiketa geometriko baten bidez lortua”. Arkiv för Matematik aldizkari suediarrean argitaratu zuten 1904an.Testuingurua ulertzeko, komeni da gogoratzea 30 urte lehenago Karl Weierstrass alemaniarrak erakutsi zuela lehen aldiz funtzio jarraitu bat ez zuena deribaturik ezein puntutan. Intuizioaren aurkako zerbait zen, puntu batzuetan deribaturik ez izan arren, besteetan (gehienetan, egia esateko) deribagarria izatea espero baitzitekeen funtzio jarraituetarako. Ohi bezala, behin portaera “patologikoa” duen funtzio bat lortuta, beste adibide batzuk ere agertu ziren.

Planoko kurbetarako deribaturik ez izatea ukitzailerik ez izatea da, norabide zehatzik ez izatea, alegia. Weierstrassen kurbaren grafikoa da, beraz, ukitzailerik inon ere ez duen kurba horietako bat. Von Kochen iritziz, bai adibide hori, bai eta geroko beste batzuk ere, analitikoki emanak ziren eta, ukitzailea izatearena edo ez propietate geometriko bat izanik, interesgarria zen geometrikoki eraikitzea halako kurba bat. Hortik bururatu zitzaion bere kurba.

Kurbak inon ere zuzen ukitzailerik ez duela ziurtatzeko, ez da nahikoa haren itxura erabat irregularra dela esatea, froga matematiko bat behar da eta horixe zen von Kochek artikuluan erakutsi zuena.

Ikuspegi fraktala

Von Kochen kurbaren luzera infinitua da. Urrats bakoitzean aurreko urratseko kurbaren luzera 4/3-rekin biderkatzen da eta limitean lortzen den kurbaren luzera infinitua da. Are gehiago, edozein bi puntu hartuta kurban, haien arteko kurba zatiaren luzera ere infinitua da. Aldiz, azalera 0 da (kurbaren azaleraz ari gara hemen).

Duela 50 urte inguru sortu zen fraktalen teoria matematikoak biziberritu zuen von Kochen elur-maluta. Luzera dimentsio bateko objektuen neurria izanik, eta azalera dimentsio biko objektuena, kurba “handiegia” zen luzerarekin neurtzeko eta “txikiegia” azalerarako. Ez da egongo “bitarteko dimentsio” bat objektu horri hobeto egokitzen zaiona? Neurrien ikuspegitik dimentsio ez-osoak aspalditik zeuden proposatuta eta modu bat baino gehiago dago dimentsio horiek definitzeko (ez denak baliokideak, gainera). Dimentsio fraktala deritzona erabiliz, von Kochen kurbari log 4/log 3= 1.2618595… dagokio.

Autoantzekotasuna

Kurbaren zati baten gainean zooma egiten badugu, kurba bera ikusiko dugu errepikatuta beste eskala batean. Hori betetzen duten objektuei “autoantzekoak” esaten zaie. Propietate hori aipatzen da askotan fraktalen ezaugarri modura, baina ez dute fraktal guztiek betetzen. Bai, ordea, von Kochen kurbak.

Hiru aipu matematikako kurba bereziei buruz

Deribaturik gabeko kurba jarraituak existitzen zirela argi geratu zen arren, ez ziren matematikari guztien gustuko objektuak. Hona hemen puntako matematikari biren iritziak:

Charles Hermite, 1893: Aldendu egiten naiz asalduraz eta izuz deribatu gabeko funtzio jarraituen zauri tamalgarri horretatik.

Henri Poincaré, 1899: Antzina, funtzio berri bat asmatzen zenean, helburu praktiko batekin izaten zen; gaur egun apropos asmatzen dira gure aiten [sic] arrazoibideak agerian uzteko, eta ez zaie inoiz hori baino gehiago aterako.

Horien ospe handia gorabehera, Jean Perrin fisikaria (1926ko Nobel sariduna) beste iritzi batekin agertu zen urte batzuk geroago. Les atomes liburu famatuaren sarreran adierazi zuen:

Jean Perrin, 1913: Matematikariek ulertu dute arrazoibide geometriko delakoen zorroztasun falta eta, esaterako, umekeria dela, kurba bat marraztuz, frogatu nahi izatea funtzio jarraitu guztiek deribatua dutela. Deribatua duten funtzioak sinpleenak eta lan egiteko errazenak izanda ere, salbuespena dira; edo, nahiago baduzue hizkera geometrikoan adierazita, ukitzailerik ez duten kurbak dira araua, eta kurba oso erregularrak, zirkunferentzia esaterako, kasu interesgarriak dira, baina oso partikularrak.

Denborak —eta matematikak— Perrini eman zion arrazoia: 1931n Stefan Banach poloniarrak frogatu zuen funtzio jarraitu “gehienak” (esanahi matematiko egoki batekin) ez direla deribagarriak.

Eta ariketa bat

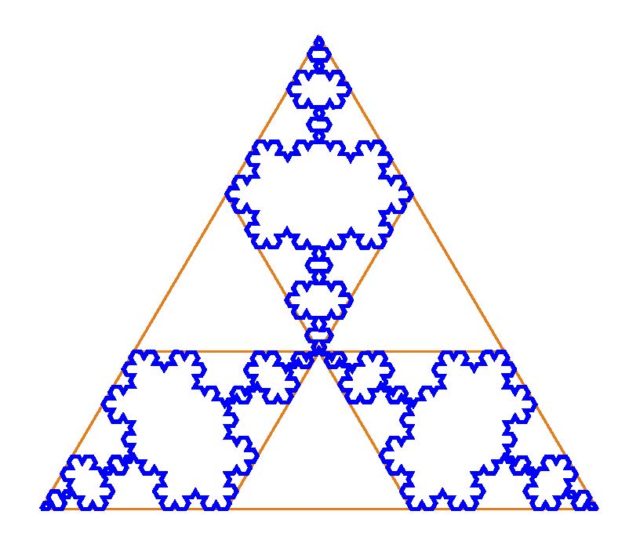
Elur-malutaren kurbak (4. irudia) eskualde bat mugatzen du planoan. Irakurle saiatuari proposatuko diodan ariketa hau da: kalkulatu eskualde horren azalera. Hasierako triangeluarena bider 8/5 lortu behar da. Barruranzko eraiketak (5. irudia) ere eskualde bat mugatzen du eta kasu horretan azalera triangeluarena bider 2/5 da.

---

Egileaz:

Javier Duoandikoetxea Analisi Matematikoko Katedradun erretiratua da UPV/EHUn.