Koronabirus berria gure eguneroko bizitzan kokatu denetik, datu-zaparrada bat heltzen zaigu egunero. Adi-adi egoten gara, pandemiaren eboluzioa jarraitu nahian. Hain zuzen, bilakaera hori erakusteko, ohikoa bihurtu da grafikoak ematea, eta egunotan entzun ditugun kurbaren pikoa edo kurba apaltzea terminoek grafikoei egiten diete aipamen. Aurkezten zaizkigun grafiko batzuetan eskala logaritmikoa erabiltzen da, eta hor goranzko urratsak ez dira proportzionalak, altuera bikoitzak ez du kopuru bikoitza adierazten, adibidez. Zer da eskala logaritmikoa eta zergatik komeni da batzuetan hori erabiltzea?
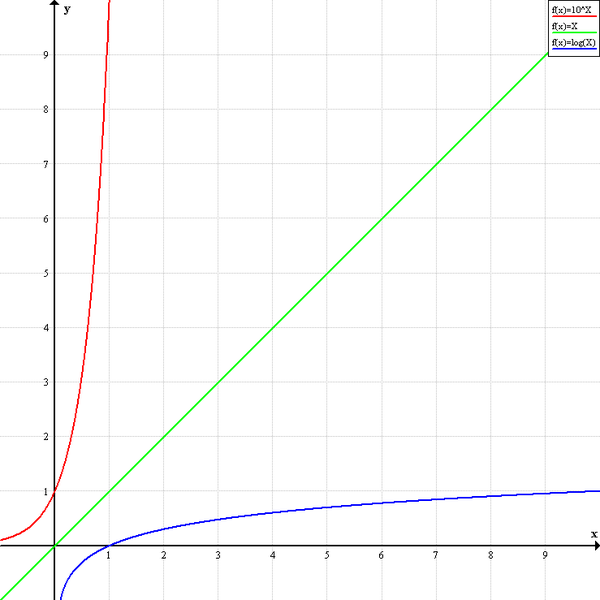
logaritmikoa (urdina). (Grafikoa: Wikimedia Commons – Creative Commons Attribution-Share Alike 3.0 Unporte lizentziapean)
Grafikoak planoan
Aipatzen ari garen grafikoak planoan egiten dira eta ardatz bi dituzte. Ardatz horizontalean aldagai bat hartzen da, denbora adibidez, eta bertikalean, neurtzen ari garen balioak. Koronabirusaren kasuan, ardatz horizontalean egunak joaten dira eta bertikalean, grafikoaren arabera, positiboak, hildakoak, sendatuak, ospitaleratuak eta abar.
Ardatz bertikalean eskala arrunta hartuz gero, eskala lineala alegia, 3tik 5era dagoen aldea eta 60tik 62ra dagoena berdinak dira. Aldiz, eskala logaritmikoan 3tik 5era dagoen aldea eta 60tik 100era dagoena dira berdinak. Alde bera egoteko, eskala logaritmikoan zenbaki bien arteko erlazioa (zatidura) berdina izan behar da (5/3=100/60). Eskala linealean kendurak dira berdinak (5-3=62-60).
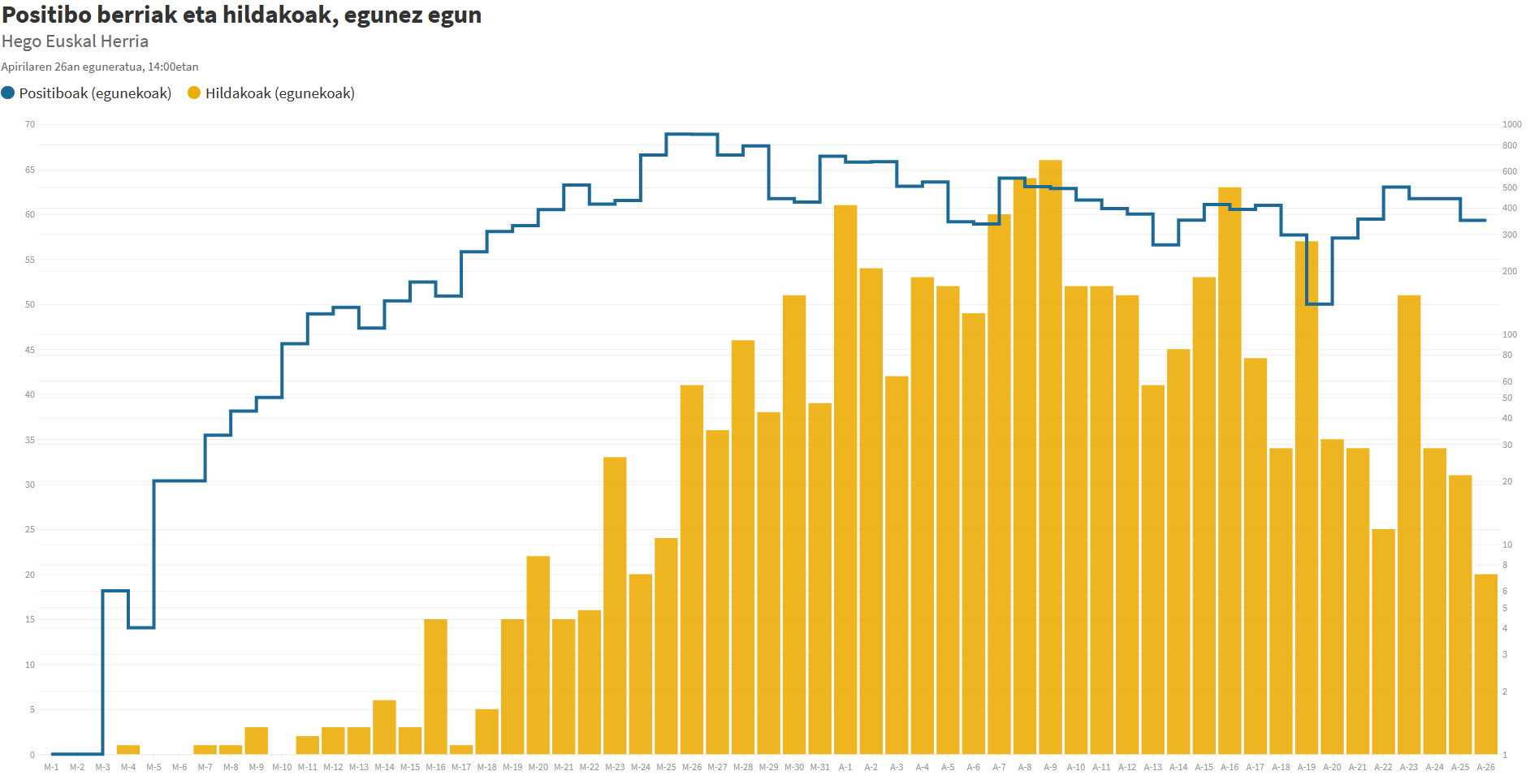
Zergatik erabili eskala logaritmikoa?
Datuen tamainaren eta azaldu nahi dugun zehaztasunaren arabera, zentzuzkoa izango da eskala logaritmikoa erabiltzea. Adibide bat jarriko dut: demagun Bizkaiko udalerrien populazioa ematen duen grafiko bat egin nahi dugula. Ardatz horizontalean herriak joango dira, bertikalean biztanle kopurua. Herriak populazioaren arabera ordenatu ditugu.
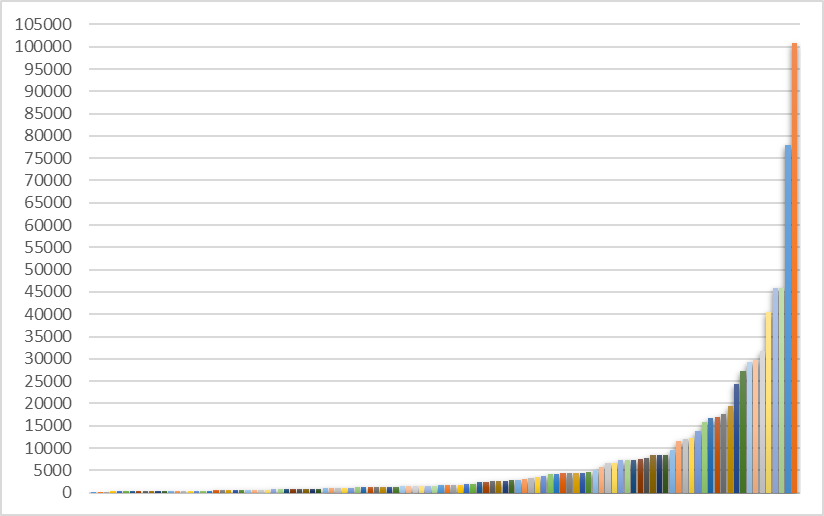
Eskala lineala erabili dugu 3. irudian eta urrats bakoitzak 5000 biztanle adierazten ditu. Bilbo kendu dugu, grafikoaren zehaztasuna are txikiagoa izango baitzen bestela. 111 udalerri daude eta handiena (Barakaldo), txikiena (Arakaldo) halako 650 da, gutxi gorabehera. Udalerri erdiak ia ikusezinak dira. Bilbo sartuz gero, grafikoko lerroen luzera heren batera txikituko litzateke, eta, ondorioz, are ikusezinago izango lirateke herri horiek eta gehiago.
Eskala logaritmikoa erabiliz, udalerri guztiak ikusiko genituzke, 4. irudiko grafikoan bezala. Hor goranzko urrats bakoitzak aurrekoaren bikoitza adierazten du.
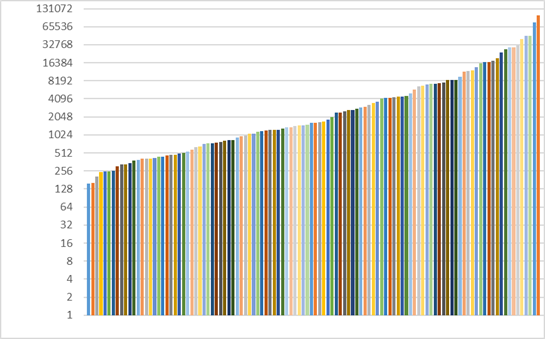
Bada beste zerbait kontuan hartzekoa: 200 biztanleko aldea garrantzitsua da herri txikietan, baina ez 10 000 biztanletik gora duen batean. Hori ere erlatibizatzen du eskala logaritmikoak. Irudian, ezkerreko herri bati 200 biztanle gehituz gero, maila bat igoko litzateke; eskuineko batek, ordea, ez luke nabarituko igoera.
Grafiko horietan barrak erabili ditugu, baina nahikoa da bakoitzean goiko puntua erabiltzea gauza bera adierazteko. Puntu horiek eratzen duten kurba eginda ere eman genezakeen grafikoa.
Zenbait propietateren portaera grafiko linealetan eta logaritmikoetan
Logaritmoa funtzio monotonoa da. Horrek esan nahi du kantitate batek gora edo behera egiten badu, berdin egingo duela gora edo behera haren logaritmoak. Horregatik ere maximo bat edo minimo bat dauden tokiak (aldagaiaren balioak) berdin mantenduko ditu grafiko logaritmikoak.
Kurba batean, maldak adierazten du hazkundearen abiadura. Horretan desberdin jokatzen dute grafikoek eskala linealean eta logaritmikoan. Koronabirusaren grafikoekin azaltzeko, egun batetik bestera 100 kutsatu gehiago gertatu badira malda bera erakutsiko luke eskala linealak bosgarren egunean gertatuta edo hogeigarren egunean gertatuta. Eskala logaritmikoan, aldiz, 100 gehiago izatea 2000 kutsatu daudenean edo 20 000 daudenean ez da berdin ikusten, bigarrenean malda hamar aldiz txikiagoa (gutxi gorabehera) izango litzateke. Hori bat dator informazio honekin: kutsatu berriak % 5 dira kasu batean eta % 0.5 bestean. (Ikus behean hirugarren ohar matematikoa.)
Adibide horrek berak balio digu ulertzeko grafikoa eman nahi dugun informazioaren arabera egokitu behar dugula. Datu metatuak ematean (kutsatu guztien eboluzioa, esaterako) grafiko logaritmikoak beharrezkoak izan daitezke, zenbaki txikiekin hasi eta handietara heldu behar dugulako (3. irudian bezala, nolabait). Kutsatu berrien kopurua jaitsi ahala, eguneko aldaketa ez da nabarituko grafiko logaritmikoan. Datu hori erakusteko, hobe litzateke datu ez-metatuak ematea eta eskala linealeko grafikoa ematea (3. irudiko grafikoko hildakoak ematen diren moduan).
Eskala logaritmikoak bizitza errealean
Musikako notak. Musikako noten ezaugarri fisikoa bibrazio-maiztasuna da. Horrela, do zentralaren maiztasuna 261.62 Hz da. Hurrengo do notaren maiztasuna bikoitza da eta aurrekoarena erdia. Zortzidun batetik hurrengora igotzea maiztasuna bikoiztea da. Eskala logaritmikoa da, beraz. Ikus azalpen gehiago Josu Lopez-Gazpioren Musikaren zientzia (II): Musika notak eta bibrazio maiztasunak artikuluan Zientzia Kaieran.
Lurrikarak. Lurrikaren intentsitatea neurtzeko, Richter eskala erabiltzen dugu. “Bertizaranen 3.7ko lurrikara bat izan da” zioen Berriak duela urtebete inguru. Aurtengo urtarrilean 7.7ko lurrikara batek astindu zuen Karibea. Bigarrena lehenengoaren bikoitza baino zertxobait gehiago bada ere (Richter eskalan), eragin dezakeen kaltea ez da bikoitza… Puntu bateko aldeak Richter eskalan 10 bider indar handiagoa adierazten du. Hau da, Karibeko lurrikara Bertizarangoa baino 10 000 aldiz indartsuagoa izan zen. Richter eskala logaritmikoa da. Beste eskala bat ere erabiltzen da lurrikaretarako, momentu magnitude eskala, hori ere logaritmikoa.
Denbora-lerro logaritmikoa. Unibertsoa sortu zenetik 13 800 milioi urte inguru joan direla esaten digute adituek. Unibertsoaren hasieran gertatu ziren aldaketak grafikoki adierazteko, denbora-lerro logaritmikoa erabiltzen da (ikus Big Bang artikulua Wikipedian).
Alderantziz ere, gaurko egunetik atzeranzko gertaerak erakusteko denbora-lerro logaritmikoa erabil daiteke, eta horrela pisu gehiago ematen diegu gugandik hurbil dauden gertaerei. Ikus irudi hau.
Adibide gehiago. Ikus Eskala logaritmiko artikulua Wikipedian.
Zenbait ohar matematiko
1. Logaritmoak definitzeko, oinarri bat behar da. Ohiko oinarriak 2 edo 10 dira, e zenbakia oinarri duen logaritmoak matematikan garrantzi berezia badu ere (logaritmo natural edo nepertar deritzo). Har dezagun 2 oinarria, adibidez. Zenbaki baten 2 oinarriko logaritmoa da 2ri jarri behar zaion berretzailea zenbakia lortzeko. Horrela, 23 = 8 denez, 8ren logaritmoa 3 da, eta 27 = 128 denez, 7 da 128ren logaritmoa. Berretzailea osoa ez bada ere defini daiteke berretura eta, horrela, edozein zenbaki positibok logaritmoa du. Hurrengo taulan zenbait zenbakiren 2 oinarriko logaritmoa agertzen da.

2. Aldagaiaren t baliorako datua u(t) idazten badugu, grafiko linealean altuera u(t)-ren proportzionala da eta logaritmikoan, aldiz, log(u(t))-ren proportzionala. Logaritmoak propietate hau du: log(a/b) = log a – log b. Horregatik, log a – log b konstantea bada, a/b da konstantea. (Logaritmoaren oinarria edozein izanda betetzen da propietatea, horregatik ez dugu adierazi.)
3. Funtzioetan (kurbetan) malda deribatua da. Baldin u(t)-ren deribatua u’(t) bada, log(u(t))-ren deribatua ku’(t)/u(t) da (k konstantea logaritmoaren oinarriaren araberakoa da). Ikusten denez, t uneko grafiko linealaren u’(t) malda u(t) balioarekin zatitzen du grafiko logaritmikoak. Zenbat eta u(t) handiagoa izan, gehiago apalduko da grafikoa.
Egileaz: Javier Duoandikoetxea Analisi Matematikoko Katedraduna da UPV/EHUn.
2 iruzkinak
Eskerrik asko aipamenarengatik, Javier.
[…] Koronabirus berria agertzeak ekarri duegunero datu pila bat jasotzea. Horien artean, grafikoak ditugu, pandemiaren eboluzioa islatzen dutenak. Horietako batzuetan, eskala logaritmikoa erabiltzen da. Bada, zer da eta zergatik komeni da hori erabiltzea? Artikulu honetan topatuko duzue erantzuna. […]