Baliteke noizbait ideia bitxiak entzun izana Interneten (edo beste komunikabideren batean), jende askok defendatuak, baina gure intuizioak onartzen ez dituenak. Hori gertatu da azkenaldian, esate baterako, COVID-19aren aurkako txertoen inguruan azaldu diren usteekin. Fenomeno horri gehiengoaren ameskeria deitzen zaio eta matematikak erabiliz (grafoen teoria eta sare konplexuen teoria, hain zuzen ere) nola aztertu ahal den ikusiko dugu.
Lehenik eta behin, definitu dezagun zer den gehiengoaren ameskeria: sare batean (sare sozial batean adibidez), gutxiengo batek duen ustea gehiengoak gehiengoaren ustetzat jotzen duenean gertatzen den fenomenoa da. Gehiengoaren ameskeria Lerman, Yan eta Wu ikertzaileek aztertu zuten lehen aldiz The “Majority Illusion” in Social Networks artikuluan. Ondo ulertzeko zertan datzan fenomeno hau, ondoko adibidea erabiliko dugu.
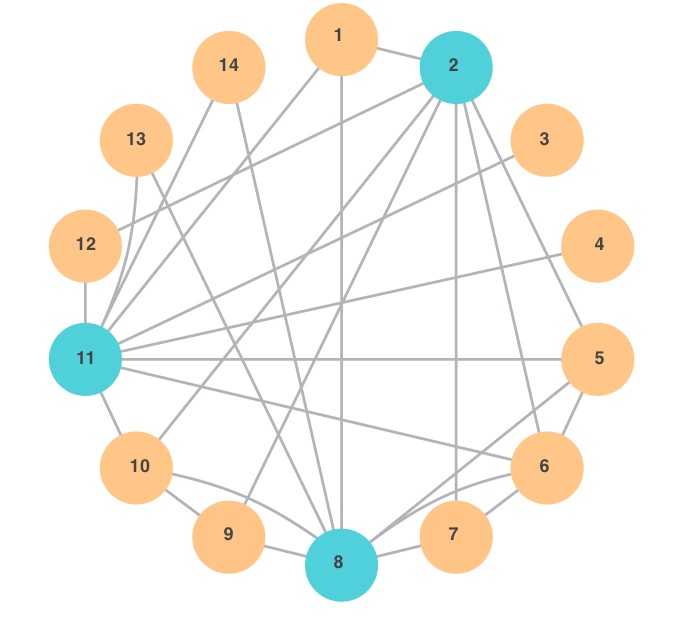
Sareak aztertzeko, grafoak erabiltzen dira normalean. Goiko irudian 14 erpineko grafo bat ikus daiteke. Grafo honetan bi motatako erpinak daude: laranjak eta urdinak. Hortaz, sare honetan bi iritzi posible daudela pentsatuko dugu (COVID-19aren txertoen aldekoa eta txertoen kontrakoa, adibidez), erpinen koloreek aldeko edo kontrako iritzia adierazten dutelarik. Alegia, kolore laranjako erpinak COVID-19aren txertoen alde daudela onartuko dugu eta kolore urdineko erpinak, berriz, txertoaren kontra. Horiek horrela, argi ikusten da gehiengoa txertoaren aldekoa dela sare honetan eta gutxiengoa kontra. Hala ere, ikusiko dugu gehiengoaren ameskeriaren fenomenoa gertatzen dela sare honetan, hau da, nodo gehienek pentsatzen dutela gehiengoa txertoen kontra dagoela.
Grafo honetako ertzek erpinen arteko harremanak adierazten dituzte. Hau da, bi erpin lotuta badaude, haien iritzia partekatzen dute beren artean (edo kontaktuak direla ere esango dugu). Hala nola, 1 erpina eta 8 erpina lotuta daudenez, 1 erpinean dagoen pertsonak ikusi ahal du zein den 8 erpineko pertsonaren iritzia, eta 9 erpinean dagoen pertsonak ikusi ahal du zein den 1 erpineko pertsonaren iritzia. Horrela, 1 erpinari galdetzen badiogu bere kontaktuen artean zein den txertoaren aldeko iritzia, haren erantzuna zein izango da? Berak, bi erpinekin lotuta dagoenez (8 erpinarekin eta 11 erpinarekin, alegia) eta bi erpin horiek txertoaren kontrakoak direnez, bere kontaktu guztiak txertoaren kontrakoak direla ondorioztatzen du. Bestalde, 5 erpinarekin gauza bera egiten badugu, konturatuko gara lau erpinekin dagoela lotuta (2 erpinarekin, 6 erpinarekin, 8 eta 11 erpinarekin, alegia) eta lau erpin horietatik hiru txertoaren kontra daudela eta bat alde. Hortaz, 5 erpinak ondorioztatzen du bere kontaktuen gehiengoa txertoaren kontra dagoela. Izan ere, grafo honetako beste erpin laranja guztiak begiratzen baditugu, konturatuko gara erpin laranja bakoitzaren kontaktu guztiak (edo gehiengoa) txertoaren kontrakoak direla. Horrela, kolore laranjako nodo bakoitzak (argi gera bedi, sare honetan dauden 14 nodoetatik 11 erpin kolore laranjakoak dira eta, hortaz, gehiengoa kolore laranjako erpinak dira) pentsatuko du txertoaren kontrako iritzia gehiengoa dela eta, arestian ikusi dugun bezala, hori ez da horrela.
Eta zergatik gertatzen da hori? Kolore urdineko erpinek kontaktu asko dituztelako eta kolore laranjakoek, berriz, gutxi. Edo grafo teoriako terminoak erabiliz, kolore urdineko erpinak gradu handiko erpinak dira eta kolore laranjakoak, ordea, gradu txikikoak. Gainera, erpin bakoitzak ezin du ikusi sare guztiaren iritzia, baizik eta beraren kontaktuena baino ez.
Argi dago goiko adibidean ez dela zaila jakitea erpin guztien iritzia (izan ere, 14 erpin besterik ez daude). Alabaina, gaur egungo sare sozialetan parte hartzen duen gizaki kopurua askoz ere handiagoa da eta sortzen den grafoaren konplexutasuna erraldoia da. Beraz, sare hauetan ezin da jakin zein den erpin guztien iritzia. Horregatik, askotan agertzen da gehiengoaren ameskeria deituriko fenomenoa gaur egungo sare sozialetan. Fenomeno honetaz baliatzen dira publizitatea egiteko, esate baterako. Izan ere, kontaktu asko duen jendeak (gradu handiko erpinak, alegia) produktuak erakusten ditu YouTubeko bideoetan eta, hori egiten dutenean, produktua jende askok ikustea lortzen dute.
Bukatzeko, gehiengoaren ameskeriari esker, okerrak diren usteak ontzat eman ahal ditugula jakinarazi nahi dizuet (goiko adibidean, txertoaren kontrako iritzia, adibidez). Horregatik, komeni da ahalik eta iturri gehienetara jotzea fenomeno baten alde edo kontrako iritzia sortu aurretik.
Erreferentzia bibliografikoa:
Lerman, K., Yan, X., Wu, X-Z. (2016). The “Majority Illusion” in Social Networks. PLoS ONE, 11(2), e0147617. DOI: https://doi.org/10.1371/journal.pone.0147617
Egileaz:
Josu Doncel Matematikan doktorea da eta UPV/EHUko Matematika Aplikatua, Estatistika eta Ikerkuntza Operatiboa Saileko irakaslea.