Grigori Perelman ez zen agertu

Javier Duoandikoetxea

Madril, 2006ko abuztuaren 22a. Matematikarien Nazioarteko Biltzarra (International Congress of Mathematicians, ICM) hastear da. Inaugurazio-ekitaldi arranditsua prestatu dute eta Espainiako Errege Juan Karlos jarri dute mahaiburu. Beste zenbait agintari ditu alboan, Nazioarteko Matematika Elkartearen (IMU) presidentearekin batera.

Jende andana elkartu da, 3 500 lagunetik gora, lau urterik behin egiten den matematikarien biltzarrik handienean. Ikusmin aparta dago eta ez preseski politikarien protokolozko hitzaldiak entzuteko. Kongresu horietan ohi den bezala, lehen egunean sariak banatzen dira, eta haien artean ospetsuenak, Fields dominak. Horrek beti sortzen badu ikusmina, oraingoa berezia da. Galdera pare bat dabil airean eta laster jakingo dugu erantzuna: emango diote saria Grigori Perelmani? Hala bada, etorriko da jasotzera?

Halako batean, John Ball, IMUko lehendakaria eta Fields dominak esleitzeko batzordearen buru izan dena, atrilera hurbildu da sarituen izenak (bi eta lau artean izaten dira) eta haien merezimenduak aipatzera. Ordena alfabetikoz irakurri ditu izenak eta bigarrena izan da Grigori Perelman, “geometriari egindako ekarpenengatik eta Ricciren fluxuaren egitura analitiko eta geometrikoari buruzko ideia iraultzaileengatik”. Ez dirudi inor altxatu denik sariaren bila eta Ball jaunak berehala zapuztu du Grigori Perelman aretoan ikusteko esperantza, “uko egin dio sariari” esanaz. Baina, zer zen berezi Perelmanen inguruan?

Zergatik ikusmin hori?

2002ko azaroan, Perelmanek artikulu bat utzi zuen Arxiv gordailuan, eta beste bi 2003ko martxoan eta uztailean. Hirurek sariaren aipamenean agertzen den Ricciren fluxuaz dihardute eta esan daiteke bigarrenak eta hirugarrenak lehena argitzen eta osatzen dutela. Arxiv artikulu zientifikoen gordailu bat da, non egileek artikuluen testuak nahi duenaren eskura uzten dituzten. Hori bai, ez dute kalitate-kontrolik pasatzen eta ez dago bermerik edukia zuzena izango den edo ez.

Usu, egileak, gordailuan uzteaz gain, aldizkari batera bideratuko du artikulua eta han, aditu batek edo gehiagok aztertu ondoren, argitaratzeko baimena emango diote edo ez. Perelmanek ez zuen bide hori hartu eta gordailuan bertan egotea nahikoa zela iritzi zion. Kontua zen, zuzen egonez gero, matematikan irekita zegoen problema handi bat, Poincaréren aierua, ebatziko zuela. Adituen kontrola gainditu arte proposamena balidatu gabe zegoen eta, gainera, lan sakona zen, arloko adituen artean ere kontuz aztertu beharrekoa. Zenbait lekutan argibideak falta omen ziren, gainera. Perelmanek Estatu Batuetara joateko gonbidapena onartu zuen eta mintegi batzuk eman zituen, lanaren lerro nagusiak jendaurrean azalduz. Hala ere, 2006ko urte hasieran, Fields dominen irabazleak erabaki behar ziren sasoian, ez zegoen baieztatuta Poincaréren aieruaren froga.

Fields domina irabazteko baldintzetako bat da jaso behar den urtean hartzaileak gehienez 40 urte izatea. Azken aukera zen Perelmanentzat 2006koa. Saria ematea erabaki zutenean, gorago aipatu dugun esaldia erabili zuten merituak arrazoitzeko; ez zioten zehazki Poincaréren aieruaren froga onartu, badaezpada ere.

Gauzak areago nahasteko, Xiping Zhu eta Huaidong Cao txinatarrek Asian Journal of Mathematics aldizkarian artikulu bat argitaratu zuten, Poincaréren aieruaren froga osoa aldarrikatu eta Perelmanen lanak hutsuneak zituela iradokitzen zuena. Eztabaida handia sortu zuen horrek, Shingtung Yau ospetsuaren babesean lortu baitzuten argitaratzea, ohiko prozedura saihestuz. Nolabaiteko plagio salaketak jasan zituzten. Azkenean, atzera egin zuten aldarrikapenean eta Perelmani aitortu zioten meritu guztia.

Fields sariaren aipamenak Poincaréren aieruaren froga zuzena zela esaten ez bazuen ere, ordurako argi zegoen Perelmanen lana garrantzi handikoa zela. Madrileko ICMn bertan hitzaldi nagusi bat prestatu zuten “Special Lecture on the Poincaré conjecture” izenburupean, John Morgan irakasle ospetsuaren eskutik. Haren lehen hitzak hauek izan ziren: “Perelmanek Poincaréren aierua frogatu du”, eta txalo zaparrada bat entzun zen. Esan daiteke lehen aitorpen ofiziala izan zela.

Fields domina jaso behar dutenei aldez aurretik jakinarazten diete aukeratu dituztela, biltzarrera joan eta bertan saria jaso dezaten. Isilpean gordetzeko ere eskatzen diete. Perelmanek sariari uko egingo ziola esan zionean IMUri, John Ball presidentea San Petersburgora joan zen harekin zuzenean hitz egitera. Ezezkoari eutsi zion Perelmanek, eta ia hori besterik ez dakigu, John Ballek ez baititu inoiz harekin izan zuen solasaldi luzearen nondik norakoak azaldu. Argitu zuen ezezkoaren arrazoiak publikoki adierazteko aukera eman arren Perelmanek horri ere uko egin ziola. Ballek gaineratu zuen arrazoiak “konplexuak” zirela eta ezin zitezkeela esaldi labur batean bildu, eta haietariko bat zela Perelmanek ez zuela komunitate baten ikur modura ikusi nahi bere burua, ez baitzen komunitate horren parte sentitzen.

Nor da Grigori Perelman

Grigori Grisha Perelman 1966ko ekainaren 13an jaio zen Leningraden, gaur San Petersburgo, familia judu batean. Ama irakasle zen eta aita ingeniari elektrikoa. Aitak 1993an Israelera emigratu zuen. Eskolako lehen urteak pasatuta, 10 zituela, amak Sergei Rukshin maisuak zuzentzen zuen zirkulu matematikora eraman zuen. Umeak matematikan trebatzeko zentro bat zen eta, han nabarmendu zenez, Perelmanek 14 urterekin Lizeo 239 izeneko ikastetxe berezira sartzeko aukera izan zuen, matematika eta fisikako aparteko programa lantzera. 1982an Soviet Batasunak Nazioarteko Matematika Olinpiadara bidali zuen seiko taldean sartu zuten. Perelmanek urrezko domina lortu zuen. 119 partaide izan zituen urte hartako olinpiadako finalak eta 42 puntu posibletik 37 edo gehiago lortu zituzten hamarrek jaso zuten urrezko domina. Perelmanek 42 puntu lortu zituen, alegia, lor zitezkeen guztiak.

Arrakasta horrek judua izateagatik izan zezakeen oztopoa gainditzen lagundu zion eta Leningradeko unibertsitatean sartu zen matematika ikastera. Behin titulua lortuta, tesia ere bertan egin zuen eta 1990ean doktore bihurtu zen.

Perelmanen lorpenek Estatu Batuetako zenbait unibertsitate ospetsurako bidea ireki zioten eta han eman zituen urte batzuk, harik eta 1995ean San Petersburgoko Steklov Institutura itzuli zen arte, ikertzaile postu batera. Bitartean, arimaren aierua izenez ezagutzen zen problema irekia ebatzi zuen eta horrek ere unibertsitate handien eskaintzak zabaldu zizkion arren, etxera bueltatzea lehenetsi zuen. 1996an European Mathematical Society elkarteak gazteentzat ematen zituen sarietako bat Perelmani esleitzea erabaki zuen, baina uko egin zion eta ez zen hartzera joan.

San Petersburgoko urte horietan artikuluak idatzi eta aldizkarietan argitaratu zituen, ohiko bidetik. Baina 2002ko lanarekin bestela jokatu zuen eta, Arxiv gordailuan eskuragarri utzita, aldizkari batean ez argitaratzea erabaki zuen. Portaera ezohikoa gorabehera, laster zabaldu zen komunitate matematikoan lanaren garrantzia. 2005ekoa izan zen Perelmanen azken agerraldi publikoa eta urte horretako abenduan uko egin zion Steklov Institutuan zeukan lanpostuari. Matematika utziko zuela esan omen zuen, eta handik aurrera ez du lanpostu jakinik izan. Espekulazioak egon diren arren, amarekin bizi dela da ziurta daitekeen gauza bakarra.

Milioi bat dolarreko saria

Clay Mathematical Institute izeneko elkartea 2000 urtean sortu zen. Hasiera entzutetsua egiteko, milioi bat dolarreko zazpi sari eskaini zituen, beste hainbeste problema hautaturen ebazpenen truke. Haietako bat Poincaréren aierua zen.

Saria lortzeko baldintza zen ebazpena aldizkari matematiko batean argitaratzea, adituen kontrola gaindituta, eta argitaratzetik urte biko epean hutsik ez aurkitzea (horrelakoak ere inoiz gertatzen baitira). Perelmanen soluzioa zuzena izanda ere, betetzen zituen ezarritako baldintza guztiak? Hura izan zen zazpi problema haietatik ebatzitako lehena (eta gaur arte, bakarra), eta Clay Institutuak baietz erabaki zuen, baldintzak betetzen zirela. Hori 2010ean izan zen eta Parisen jardunaldi bat antolatu zuten Poincaréren aieruaren inguruko zenbait hitzaldirekin. Hantxe emango zioten Perelmani milioi bat dolarreko saria. Baina Grigori Perelman ez zen agertu eta uko egin zion sariari, berriro ere. Oraingoan, ordea, dirutan sari mamitsua zen, Errusian lanik egin gabe urte luzez bizitzeko adinakoa, seguruenik. Dirudienez, Perelmanek erantzun zuen ez zela bidezkoa saria berari bakarrik ematea, Richard Hamiltonen ekarpena ere kontuan hartu behar zela eta berak beste meritu zuela. Hain zuzen ere, Hamilton izan zen 1980ko hamarkadan Ricciren fluxua aztertzeko bidea zabaldu zuena, Poincaréren aieruari begira. Programa horren azken urratsa Perelmanek burutu zuen.

Poincaréren aierua

Henri Poincaré (1854-1912) frantsesa matematikaren historiako izen handienetako bat da. Esaten da hura izan zela azken matematikari unibertsala, matematikaren alor guztiak ezagutzen zituela, alegia. Topologia aljebraikoa deritzon adarra berak sortu zuen nolabait, eta hor kokatzen da hizpide dugun problema.

Har dezagun dimentsio biko esfera bat, baloi baten azala, esaterako. (Hiru dimentsioko espazioan kokatzen dugun arren, gainazalak berak dimentsio bi ditu. Gogoratu Lurrean puntu bat lokalizatzeko longitudea eta latitudea behar direla, koordenatu bi, alegia.) Esferan kurba itxi sinple bat —puntu batetik bi aldiz pasatzen ez dena— hartzen badugu, era jarraituan deformatuz puntu batera eraman dezakegu. Era jarraituan egiteak esan nahi du ezin dezakegula apurtu. Dimentsio biko beste gainazal batzuek ere propietate hori bera dute, baina ez guztiek. Adibide bat emateko, har ezazue pneumatiko baten gainazala (toroa deitzen diogu matematikan). Irudian markatutako zirkunferentziak ezin dira apurtu barik puntu batera eraman. Poincarék frogatu zuen esferarako aipatu dugun propietate hori bera duten gainazal itxi eta ertzik gabeko guztiak topologikoki baliokideak direla, hau da, deformazio jarraituen bidez esfera batera eraman daitezkeela.

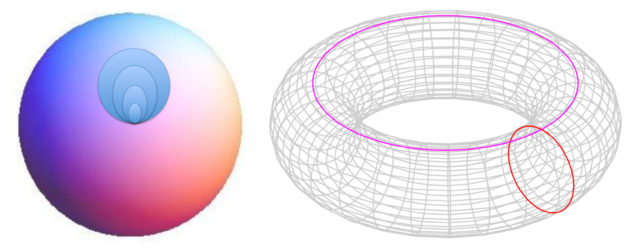
Behin dimentsio biko esferetarako ikusita, hiru dimentsiokoei ekin zien. Hiru dimentsioko esfera lau dimentsioko espazioan kokatu beharko genuke, eta ez dugu hori marrazki baten bidez erakusterik. Hala ere, zentzua du: lau dimentsioko espazioan puntu batetik distantzia finko batera dauden puntuek osatzen dute hiru dimentsioko esfera bat. Bada, hiru dimentsioko gainazaletarako (edo barietateetarako, ohiko termino matematikoa erabiliz) ere frogatu nahi izan zuen Poincarék propietate bera: kurba itxi sinpleak modu jarraituan puntu batera eramatea onartzen duten hiru dimentsioko barietate itxi eta ertzik gabeko guztiak esferaren baliokideak dira, hau da, deformazio jarraituen bitartez esfera bihur daitezke. Ez zuen lortu frogatzea eta problema modura geratu zen. Horixe da Poincaréren aierua, 1904tik zabalik egon zen problema.

Galdera dimentsio handiagoetarako ere egin daiteke, jakina. Pentsa zitekeen hiru dimentsiorako erantzunik gabe egonda zaila izango zela gorago joatea. Aitzitik, ez zen hala gertatu. 1960ko hamarkadan bost dimentsiotik gorako kasuetan aierua betetzen zela frogatu zuen Stephen Smale estatubatuarrak eta 1966ko ICMn Fields domina jaso zuen. Hogei bat urte geroago, Michael Freedman estatubatuarrak egiaztatu zuen emaitza lau dimentsioko barietateetan eta hark ere Fields domina irabazi zuen, 1986an. Horrenbestez, jatorrizko hiru dimentsioko galdera gertatu da zailena, uste orokorraren aurka. Beste hogei urte iragan ziren Perelmanek Richard Hamiltonek hasitako bidea burutu eta behin betiko ebatzita utzi zuen arte.

ICM 2022

2022 ere Matematikarien Nazioarteko Biltzarra egiteko urtea izan da. Biltzarra non egingo den lau urte lehenago erabakitzen da eta aurtengoa San Petersburgori esleitu zioten. Hara non ICM Perelmanen etxe albora joango zen. Aukera ezin hobea Perelman bera ICMra hurbiltzeko. Seguru asko inork ez zuen pentsatzen hala gertatuko zenik…

Nolanahi ere, ez da modurik izan egiaztatzeko gizona ezustekoa emateko prest ote zegoen. Munduko egoera politikoak horretan ere eragin du eta Ukrainako inbasioaren ondorioz, biltzarra ez da San Petersburgon izan. Han ez egiteko erabakia aurtengo otsailean hartu zenez, ez zegoen astirik beste egoitza batean antolatzeko. Varsovian 1982an egin behar zen biltzarra ere urtebete atzeratu zen, Poloniaren orduko egoera politikoagatik. Oraingoan, ordea, teknologiaren aurrerapenak beste aukera bat eman die antolatzaileei: kongresu birtuala izan da, hizlariek nork bere lekutik hitz egin dute eta edozeinek ikusi ahal izan ditu hitzaldiak etxeko gailuan. Sariak emateko ekitaldia zuzenean egin zen Helsinkin, irabazleak bertan zirela, uztailaren 5ean. Ez, ordea, ohikoa izaten den bezala biltzarkide guztiak aurrean izanda.

Beste lau matematikari batu zaizkie aurten Fields dominaren irabazleei: Hugo Dominil-Copin frantziarra, June Huh jatorri korearreko estatubatuarra, James Maynard britainiarra eta Maryna Viazovska ukrainarra. Azken hau izan da saria jaso duen bigarren emakumea. Ez dezala inork bilatu azken momentuko arrazoi politikorik sari horren atzean, duela lau urte ere denen ahotan baitzen Viazovskaren hautagaitza.

Azken iruzkina

Ez dut diruan eta ospean interesik. Ez dut erakusleiho batean agertu nahi, zoo bateko animalia baten moduan. Ez naiz matematikako heroia. Ez naiz hain arrakastatsu ere, horregatik ez dut nahi denak niri begira egotea.

Ez nago ados matematikaren komunitate antolatuarekin; ez zaizkit gustatzen hartzen dituen erabakiak, bidegabeak iruditzen zaizkit.

Hitz horietan ikusten da Perelmanen jarrera, neurri batean, matematika ofizialaren kontrako erreakzioa zela. Hori guztia kontuan hartuta, batzuek txalotu egin zituzten haren erabakiak eta haren ospe eztabaidaezinean establishment-ari astindua emateko liderra ikusi zuten. Perelmanek, baina, ez du urratsik egin norabide horretan, ezkutatu egin da eta isilik mantendu. Utzi egin du matematikaren mundua, ez da saiatu ezer aldatzen. Ez dirudi haren bideak jarraitzaile asko dituenik ere.

---

Egileaz:

Javier Duoandikoetxea Analisi Matematikoko Katedradun erretiratua da UPV/EHUn.