Dozena erdi ariketa 2024ko udarako (6): triangelua biratu
Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta aurten ere, udako oporretan egiteko asteazkenero ariketa matematiko bat izango duzue, Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.
Hona hemen gure seigarren ariketa:
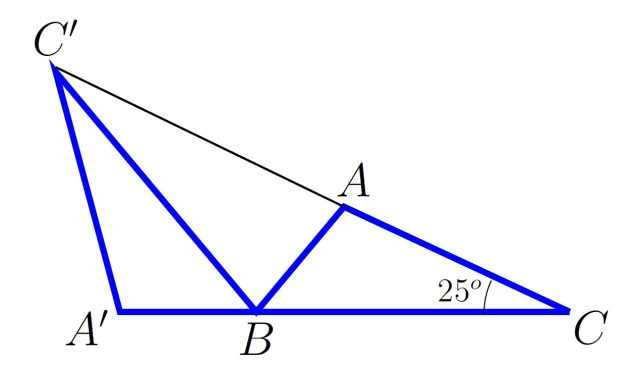
Egurrezko ABC triangelua dugu mahai gainean. C erpineko angelua 25º-koa da. Triangelua birarazi dugu, B erpina finkatuta, A’BC’ posiziora heldu arte, non A’, B eta C lerrokatuta dauden. Hori egin dugunean, C, A eta C’ ere lerrokatuta geratu dira. Zein da B erpineko angeluaren neurria?
Zein da erantzuna? Idatzi emaitza iruzkinen atalean (artikuluaren behealdean daukazu) eta, nahi izanez gero, zehaztu jarraitu duzun ebazpidea ere. Irailean emaitza zuzenaren berri emango dizugu.
Ariketak “Calendrier Mathématique 2024. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.
3 iruzkinak
Hona hemen nire ekarpena.
Hiru ángelu ditugu, 25º, a, b eta g. Non g den biratutako angelua.
Planteatu dezaket hiru ekuazio;
1) 25+a+b=180
2) 25+b+g+(b-25)=180
3) a+b+(100-a)+3+g=360
Honek ematen dit soluzio bezela; b=12,5 , a=142,5 eta g=155.
Nire uztez ebazpena da b=12.5
Kaixo, hemen doa nire proposamena:
Problema honetan, hiru triangelu erabiliko ditugu: ABC eta A’BC’ triangelu kongruenteak (berdinak) eta CA’C’ triangelua.
ABC triangelua B erpinaren inguruan biratzean, berarekin kongruentea (berdina) den A’BC’ triangelua sortzen da. Orduan zera dugu:
A’BC’ triangeluan C’ erpineko angelua = ABC triangeluan C erpineko angelua = 25º eta BC aldea = BC’ aldea, hortaz, CC’B triangelua isoszelea da; ondorioz, CC’B triangeluan C’ erpineko angelua = 25º
Orduan,
CA’C’ triangeluan C’ erpineko angelua = 25º+25º = 50º eta C erpinekoa 25º, beraz, A’ erpinekoa 180º-25º-50º = 105º
Azkenik,
A’BC’ triangeluan B angelua = 180º-25º-105º = 50º; eta hauxe da B erpineko angelua ere ABC triangeluan.
Tarteka heldu ahal izan diot proposatutako problemak ebazteari, baina merezi izan du. Emaitza zuzena lortzeak baino garrantzi handiagoa du pentsatzeak, eta, gainera, osasungarria da.
Hurrengora arte, eskerrik asko!
Kaixo, hemen doa azalpen bat:
Hiru triangelu erabiliko ditugu: ABC eta A’BC’ triangelu kongruenteak (berdinak) eta CA’C’ triangelua.
ABC triangelua B erpinaren inguruan biratzean, berarekin kongruentea den A’BC’ triangelua sortzen da. Orduan zera dugu:
A’BC’ triangeluan C’ erpineko angelua = ABC triangeluan C erpineko angelua = 25º eta BC aldea = BC’ aldea, hortaz, CC’B triangelua isoszelea da, eta ondoroz, CC’B triangeluan C’ erpineko angelua = 25º
Orduan,
CA’C’ triangeluan C’ erpineko angelua = 25º+25º = 50º eta C erpinekoa 25º, beraz, A’ erpinekoa 180º-25º-50º = 105º
Azkenik,
A’BC’ triangeluan B angelua = 180º-25º-105º = 50º; hauxe da, B erpineko angelua ere ABC triangeluan.
Hurrengora arte, eskerrik asko!