Lorategi metaforiko horiek matematika modernoko objektu nagusi bilakatu dira.
1940. urtean, alemanek preso hartu zuten Jean Leray matematikari eta artilleriako ofiziala. Baina Lerayk topologoa zela esan zien; izan ere, beldurra ematen zion bere benetako espezialitatea hidrodinamika zela esateak, gerran alemanei laguntzera behartuko zutelakoan. Preso egon zen ia bost urteetan, Lerayk engainuari eutsi zion, eta topologian, forma deformagarriak aztertzen dituen matematikaren adarrean, ikertzen aritu zen. Eta, azkenean, matematika modernoen ideia iraultzaileenetako bat sortu zuen: “sorta” kontzeptua.

1950eko eta 1960ko hamarkadetan Alexander Grothendieckek Lerayren nozioa ezagutzera eman ondoren, sortek “rol nagusia” hartu zuten matematikan, eta “geometria aljebraiko modernoan tresna oinarrizkoenetako bat bihurtu ziren”; halaxe adierazi du Texaseko Unibertsitateko (Austin) David Ben-Zvik.
Hasierako azalpen batek dioenez, sortak beste objektu matematikoen gainean eraikitako garapentzat har daitezke. “Imajinatu objektu matematikoa lurzati bat dela eta sorta haren gainean dagoen lorategia”, azaldu du Mark Agriosek.
Sortei izen hori eman zitzaien azpiko objektu bati “zurtoinak” lotzea inplikatzen dutelako. Lerayk “faisceaux” izendatu zituen, horien itxurak bildutako gari-sortak gogorarazten zizkiolako. Lorategiak lur mota ezberdinetan haz daitezkeen modu berean, sortak ere objektu matematiko anitzen gainean eraiki daitezke; eta, beraz, askotariko formak har ditzakete.
Sorta sinpleenak ere entitate matematiko nahiko konplikatuak dira. Hobeto ulertzeko, sorta bat eraikiko dugu. Hementxe azaltzen da nola egin daitekeen sorta sinple bat lerro zuzenetatik abiatuta.
Azpiko objektua zenbaki errealen lerroa izango da:
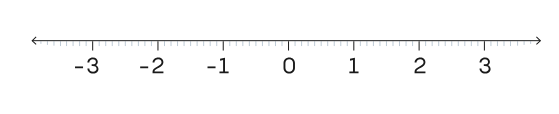
Eta sorta bat eraikiko dugu tarteetatik abiatuta, puntu indibidualetatik abiatu ordez. Zenbakien lerroa modu infinitutan bereiz daiteke tarteetan. Hona hemen adibide bat.

Parentesi bikote bakoitzaren artean horien arteko puntu guztiak —muturrak izan ezik—barne hartzen dituen tarte bat dago. Hortaz, (0, 1) tarteak zero baino handiagoak eta 1 baino txikiagoak diren zenbaki guztiak barne hartzen ditu.
Sortak tarte guztiak barne hartzen ditu, ez soilik horietako bat. Tarte bakoitzari “sekzioen” multzo bat eslei dakioke. Adibide honetan, sekzioak tarte batetik igarotzen diren lerro zuzen posible guztiak dira.
Har dezagun tarte bakar bat, jarraian erakusten den moduan. Sekzioetako hiru bakarrik agertzen dira; izan ere, ezinezkoa da denak aldi berean bistaratzea.
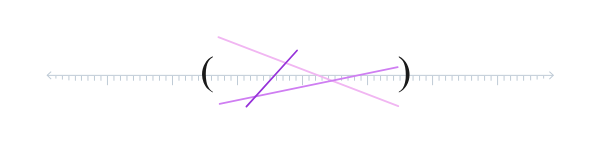
Sortak tarte posible guztien sekzio guztiak eta tarte horien loturak barne hartzen ditu.
Entitate benetan kaotikoa da, baina matematikoki oso erakargarria da, azpian oso sinplea den zerbait ezkutatzen duelako. Aurreko irudian, tarte ezberdinetarako hautatutako sekzioek talka egiten dute. Lerroak bata bestearen gainetik eta azpitik igarotzen dira, bat egin beharrean.
Matematikariek ulertu nahi dute zer gertatzen den tarte bakoitzeko sekzio bat hautatu eta sekzioak elkarren artean bateragarriak izatearen eskakizuna ezartzen denean, gainjarritako tarteak bat etor daitezen. Muga hori aplikatuta, harritzekoa den zerbait gertatzen da.
Tarte bat beste baten barruan habiaratuta baldin badago, lerroek bat etorri behar dute gainjartzean.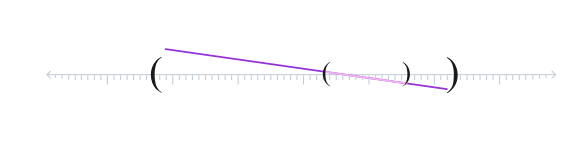
Eta muga lokal horretatik abiatuta, ondorio global bat lortzen da: lerro txiki asko lortu beharrean, habiaratzearen araua betetzen duten aukera posible bakarrak lortzen dira; alegia, zenbakien lerro osoan zehar jarraitzen duten lerro zuzenak.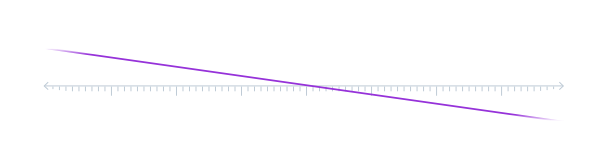
Eta lerro horiei sekzio global esaten zaie. Sorten ezaugarri nagusietako bat da objektu global horiek mugapen lokaletatik sortzen direla.
Honako hau lerro zuzenen sortaren edo funtzio linealen benetako lerroaren gaineko ibilbide bat da. Sorta sinpleenetako bat da.
Benetako lerroaren gainean sorta asko sor daitezke. Horren analogia izan daiteke lore ezberdinak landatzea lurzati berean. Sortetako bateko funtzioen grafikoek ez dute saltorik, beste sorta bateko funtzioen grafikoek ez dute kurba akuturik eta horrela infinitura arte jarrai dezakegu.
Baina hori guztia hasiera besterik ez da. Lore ezberdin bat landatu ordez, beste lurzati bat zain genezake. Imajinatu sorta bat eraikitzen duzula zirkulu baten gainean, lerro baten gainean eraiki ordez. Horrek altuera infinituko zilindro moduko egitura bat sortuko du. Zilindro horretan marraztutako objektuen egitura sorta zehatz baten eraikuntza zehatzaren araberakoa da.
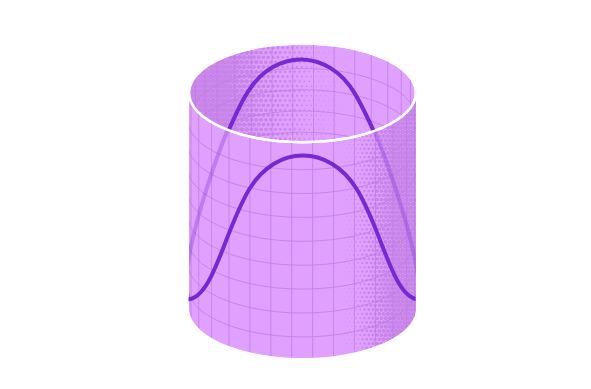
Puntu horretara arte, aipatu ditugun sorta guztiak funtzioen familiak ziren. Baina sortak (askoz ere) konplikatuagoak izan daitezke.
Aurreko irudiko zilindroa altuera infinituko laukizuzen baten emaitzatzat har daiteke, haren aldeak itsatsi ondoren. Aldiz, laukizuzenaren alboak biratuko bazenitu horiek itsatsi aurretik, hurrengo irudian bezalaxe, zabalera infinitua duen Möbius banda bat sortuko zenuke (ez da posible halakorik marraztea eta, beraz, zabalera finitua duen Möbius banda bat jarriko dugu). Möbius banda horretan, grafikoen antzeko kurbak marraz daitezke oraindik.

Zirkuluaren edozein zati lokaletan, kurba horrek funtzio baten grafikoa dirudi. Baina eskala globalean, ez da funtzio bat. Izan ere, ezin da koordenatuen sistema global kontsistente bat definitu, tortsioa dela eta (zerrenda osoaren ibilbideari jarraitzen saiatzen bagara, gure goiko eta beheko nozioak alderantzikatzen dira, eta ezinezko suertatzen zaigu). Matematikariek «funtzio tortsionatu» izendatzen dituzte objektu horiek.
Sorta bakoitza objektuen bilduma zabala bada ere, sorta guztien bilduma objektu matematiko emantzat jo daiteke: benetako lerroa, zirkulua edo beste entitateren bat. Horren analogoa litzateke lurzati zehatz batean landa litezkeen lorategi posible guztiak kontuan izatea. Horrek informazioa emango digu lurrari buruz. Lurzati batzuk oihan tropikalak dira, eta beste batzuk basamortuak. Posible diren sortak deskubritzeak aukera ematen die matematikariei azpiko espazioaren egitura ikertzeko, lurzoru jakin batean zein landare hazten diren jakiteak lurzoru horri buruzko informazioa ematen digun bezalaxe.
Grothendiecketik aurrera, matematikariak gradualki ohartu ziren sorten bildumak oso antzekoak direla funtzioen bildumekiko, baina konplexutasun maila handiagoarekin. Sortak batu eta biderka daitezke, baita horiekin kalkulu bertsio bat egin ere.
Preso zegoela, Lerayk atera ireki zuen mundu matematiko erabat berri batera.
Jatorrizko artikulua:
Konstantin Kakae (2024). What Are Sheaves?, Quanta Magazine, 2024ko uztailaren 19a. Quanta Magazine aldizkariaren baimenarekin berrinprimatua.