Matt Strassler fisikariak Waves in an Imposible Sea (Uhinak ezinezko itsaso batean) liburu berritik egokitutako artikulu honetan azaltzen duenez, masak unibertsoan duen jatorriak zerikusi handia du musikarekin.
2012an Higgsen bosoia Hadroien Talkagailu Handian aurkitu izanak berretsi egin zuen partikulen fisikariok aspalditik susmatzen genuena: kosmosa sartzen den eta oinarrizko partikulen masak sortzen dituen eremu bat dagoela. Zoritxarrez, fisikarientzat zaila izan da gainerakoei azaltzea Higgsen eremu deitzen den horrek nola betetzen duen bere zeregin handia.
Ikuspegi komun bat istorio fantastiko bat kontatzea izan da. Hona hemen bertsio bat:
Bada substantzia bat, zopa baten modukoa, unibertsoa betetzen duena; hori Higgsen eremua da. Partikulak mugitzen diren heinean, zopak balaztatu egiten ditu, eta horrela hartzen dute masa partikulek.
Beste bertsio batzuk Higgsen eremua melaza bat, sastraka bat, jende asko edo elur hedadura baten antzeko zerbaiten moduko gisa deskribatzen dute.
Hala ere, istorio horiek guztiak ez datoz bat fisikariok lehen urteko unibertsitate ikastaroen lehen asteetan irakasten dugunarekin. Higgsen eremuak egindako erresistentziaren eraginez masa sortzen duela iradokitzean, Newtonen mugimenduaren lehen eta bigarren legeak hausten dira. Beste hondamendi batzuen artean, erresistentzia horrek aspaldi eragingo zuen Lurra Eguzkirantz kiribil batean erortzea. Gainera, Higgsen eremua benetan substantzia bat balitz, gure mugimendu absolutua neurtzeko konparazio puntu bat izango litzateke, Galileoren eta Einsteinen erlatibitatearen printzipioak urratuz.
Egia esan, Higgsen eremuak ez du zerikusirik mugimenduarekin, ezta desazelerazioarekin ere; bere historia guztia bibrazioaren ingurukoa da.
Eremuen teoria kuantikoak, partikulen fisika modernoaren esparru ahaltsuak, unibertsoa eremuz beteta dagoela dio. Horren adibide dira eremu elektromagnetikoa, grabitazio eremua eta Higgsen eremua bera. Eremu bakoitzerako, dagokion partikula mota bat dago, eremu horretako uhin txiki gisa hobeto ulertzen dena. Eremu elektromagnetikoaren uhinak argi uhinak dira, eta haien uhin leunenak argi partikulak dira, eta horiei fotoi deitzen diegu. Era berean, elektroiak uhinak dira elektroien eremuan, eta Higgsen bosoia uhin txiki bat da Higgsen eremuan.

Elektroi egonkor bat, gitarra soka baten bibrazioa bezala, uhin geldikor bat da, nahi duen maiztasunarekin bibratzen duena, erresonantzia maiztasun gisa ezagutzen dena. Erresonantzia bibrazio hori ohikoa eta familiarra da. Pultsatutako gitarra soka batek erresonantzia maiztasuna etengabe jotzen duenez, beti tonu bera sortzen du. Era berean, pendulu kulunkatzaile baten maiztasun finkoak bihurtzen du erloju bat eraginkor. Printzipio beraren arabera, elektroi egonkor bakoitzak eremu elektronikoaren erresonantzia maiztasunarekin bibratzen du.
Unibertsoko eremu gehienek erresonantzia maiztasunak dituzte. Zentzu batean, kosmosak musika tresna baten antza du; biek dituzte maiztasun bereizgarriak, eta horietan errazago bibratzen dute.
Niretzat, pertsonalki, errealitatearen oinarria erresonantzia izateak atsegina eta harridura sortzen dit. Musikari eta konpositore afizionatua naizen aldetik, aspalditik ezagutzen dut pianoen, klarineteen eta gitarren barne funtzionamendua. Baina erabat harrituta geratu nintzen, graduondoko ikaslea nintzenean, unibertsoaren egiturek, baita neure gorputzaren barruan ere, antzeko printzipioen arabera funtzionatzen dutela ezagutzean.
Hala ere, gure kosmosaren musikaltasun sekretu hori ezinezkoa litzateke Higgsen eremuagatik ez balitz.
Eremuen teoria kuantikoan, Einsteinen fisika kuantikoaren eta erlatibitatearen konbinazio batek erresonantzia maiztasun baten eta oinarrizko partikula baten masaren arteko erlazio erabakigarri batera garamatza: partikula geldikor batek zenbat eta azkarrago bibratu, orduan eta handiagoa da bere masa. Erresonantzia maiztasunik ez duten eremuak masarik ez duten partikulei dagozkie; partikula horiek, eremu elektromagnetikoko fotoiak barne, ezin dute inoiz egonkorrak izan.
Higgsen eremuari buruzko fantasiazko ipuinek masa oinarrizko partikulen desazeleraziotik sortzen dela iradokitzen badute ere, melazaren antzeko substantzia batengatik, egia esan, Higgsen eremu indartsuago batek oinarrizko partikulak maiztasun altuagoetan bibrarazten ditu, eta horrek masa handitzen du. Beraz, Higgsen eremua errefortzuko eragile kosmiko moduko bat dela esan daiteke, beste eremu batzuetako erresonantzia maiztasunak handitzea helburu duena.
Nola alda dezake eremu batek bestearen maiztasuna? Pendulu xumeak adibide erraz bat eskaintzen digu.
Demagun pilota bat soka baten muturrean jartzen dugula espazio sakonean, non grabitazio eremua ia nulua den. Pilotak norabide finkorik gabe flotatuko du. Pixka bat bultzatzen badugu, bere posizioa poliki-poliki alda daiteke, baina ez du bibraziorik izango.
Hala ere, pendulu inprobisatua zero ez den grabitazio eremu batean jartzen bada, dena aldatzen da. Bola zuzen zintzilikatzen da beherantz, eta mugitzen bada, kulunkatu egiten da.
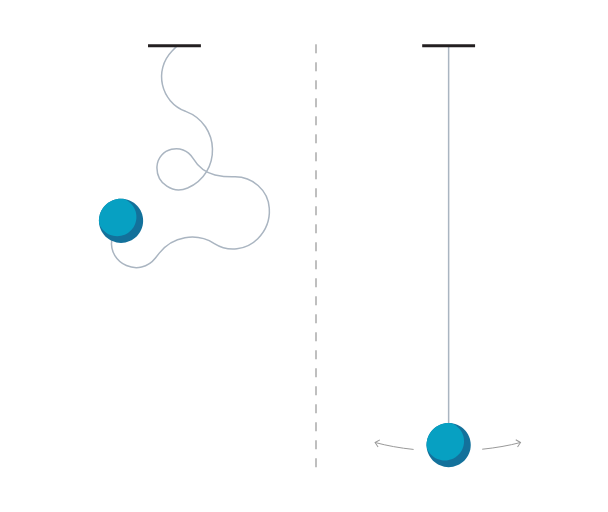
Pilota geldirik dagoenean, orekan dagoela esaten da: egonkorra, orekatua eta mugitzeko arrazoirik gabe. Pilota eskuinerantz mugitzen bada, grabitateak ezkerrerantz kulunkatzea eragingo du, eta alderantziz. Pilotaren posizioak oreka puntura itzultzeko duen joerak, leheneratze efektu gisa ezagutzen denak, kulunkatzea eragingo du.
Kasu horretan, grabitazio eremuak errefortzu eragile gisa jokatzen du: pendulua zurrunago bihurtzen du, eta horrek erresonantzia maiztasun bat ematen dio, zero ez dena. Grabitazio eremua zenbat eta indartsuagoa izan, orduan eta indartsuagoa izango da berreskuratze efektua, eta penduluaren erresonantzia maiztasuna handiagoa izango da.
Era berean, Higgsen eremuak leheneratze efektua sortzen du oinarrizko beste eremu batzuetan, eta horrek duten bibratzeko modua aldatzen du. Nahiz eta edozein eremuk izan ditzakeen mugitzen diren uhinak, urmael bat zeharkatzen dutenak bezalakoak, leheneratze efektu batek ahalbidetzen du eremu batek uhin geldikorrak izatea, gitarra soka batean agertzen diren uhin geldikorren antzekoak. Lehen aipatu dudan bezala, uhin geldikor horiek geldirik dauden oinarrizko partikulak besterik ez dira, bakoitza bere eremuan kulunkatuz.
Ideia hori Peter Higgs (Higgen eremuaren homonimoa) fisikari britainiarra zenak eta haren lehiakideek 1960ko hamarkadan adierazi zutenaren muinean dago: eremu batek beste eremu batzuk indartu ditzake, eta, horrela, uhinek beren lekuan erresonantzia maiztasunarekin bibratzen dute; eta, horrek, beren partikulei masa ematen die. Higgsen bosoiaren ikerketa esperimentalek, Hadroien Talkagailu Handian, baieztatzen dute hori dela hain zuzen ere Higgsen eremuak egiten duena. Partikulen fisikaren eredu estandarraren matematika erabiliz (ezagutzen diren oinarrizko partikula guztiak eta unibertsoko eremuen arteko elkarrekintzak deskribatzen dituen eremuen teoria kuantikoa), zientzialariek Higgsen bosoiaren portaerari buruzko iragarpenak egiten dituzte, eta esperimentuekin guztiz bat datoz. Ez dago zalantzarik: Higgsen eremuak leheneratze efektua sortzen du beste eremu askotan.
Beraz, Higgsen eremua sakonago ulertuta, beste istorio bat iradokiko dizuet:
Bazen behin existitu zen unibertso bat. Bero kiskalgarria, oinarrizko partikulaz gainezka. Bere eremuen artean Higgsen eremua zegoen, hasiera batean itzalita zegoena. Baina unibertsoa hedatu eta hoztu ahala, Higgsen eremua bat-batean aktibatu zen, zero ez zen indar bat garatuz. Hori gertatu zenean, eremu asko zurrun bihurtu ziren eta, ondorioz, haien partikulek erresonantzia maiztasunak eta masa hartu zuten. Horrela bihurtu zen unibertsoa, Higgsen eremuaren eraginaren bidez, gaur egun den musika tresna kuantikoa.
Jatorrizko artikulua:
Matt Strassler (2024). How the Higgs Field (Actually) Gives Mass to Elementary Particles, Quanta Magazine, 2024ko irailaren 3a. Quanta Magazine aldizkariaren baimenarekin berrinprimatua.