Catalanen zenbakiak
Segida matematikoak arau bat jarraitzen duten zenbaki multzoak dira. Adibiderik ezagunena Fibonacci-ren segida da. Fibonacci-ren segida era honetan definitzen da: a0=1 eta a1=1 badira, orduan bat baino hertsiki handiagoa den edozein n-rako, an=an-1+an-2 izango da. Segida hori untxi kopurua aztertzeko erabili zuen Fibonacci-k, baina urteak pasatu ondoren, segida horren beste hainbat aplikazio aurkitu dira, batez ere naturan (ikusi loreetako adibidea: esteka).
Artikulu honetan beste segida matematiko bat ikusiko dugu, Catalanen zenbakiak alegia. Segida matematiko hori Eugene Charles Catalan matematikari belgikarrak asmatu zuen. Segida ulertzeko, adibide bat ikusiko dugu.
Demagun n x n tamainako taula bat dugula (xake taula bat esate baterako). Taula horretako behean eta ezkerrean dagoen izkinetik goian eta eskuinaldean dagoen izkinera joan nahi dugula pentsatuko dugu. Horretako, bakarrik eskuinera edo gora jo ahal dugu eta eta ezin dugu taularen diagonala gurutzatu. Gure helburua lortzeko behar den mugimendu kopurua n-ren araberakoa izango da. Horrela, 1 x 1 tamainako taularen kasuan, modu bakarra dago; lehenik eskubitara eta gero igotzea (ikusi azaldutako bidea gorriz).

Aldiz, 2 x 2 tamainako taula bat kontuan hartzen badugu, bi modu ezberdinez lortu ahal dugu gure helburua, beheko irudietan ikusten den bezala.
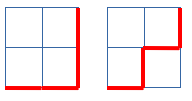
Gainera, 3 x 3 tamainako taula bat hartuz gero, 5 modu ezberdinez lortu daiteke gure helburua:

Eta zenbat modu ezberdinez egin daiteke 15 x 15 tamainako taula bat kontuan hartzen badugu? Catalanen zenbakiak erabiliz, erantzuna 9.694.845 dela ikusiko dugu artikulu honetan.
Beste adibide bat ikusiko dugu orain. Suposatu n aldeko poligono bat dugula eta jakin nahi dugu zenbat modu ezberdinetan triangulatu daitekeen (gogoratu poligono bat triangulatzea hirukiz osatzea dela). Alegia, hiruki bat edukiz gero, modu bakarrean triangulatu daiteke, baina karratu bat bi modu ezberdinetan (ikusi beheko irudiak).
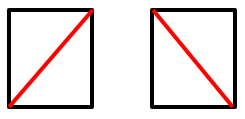
Orain, pentagono bat dugula pentsatuko dugu eta, kasu honetan, 5 modutan triangulatu ahal dela ikusten da beheko irudian:

Beraz, 18 aldeko poligono bat zenbat modutan triangulatu daiteke? Catalanen zenbakiak erabiliz, kasu honetan ere erantzuna 9.694.845 dela ikusiko dugu.
Konbinatoria matematikako arlo bat da, kontaketak aztertzen dituena. Konbinatorian erabiltzen den kontaketa-metodorik ezagunetariko batek errekurtsibitatean du oinarri; alegia, zaila den problema bat ebazteko, haren bertsio sinpleagoaren soluzioa erabiltzea. Horrela, bertsio sinpleetan kontaketa egitea erraza dela kontuan hartuz, metodo errekurtsiboarekin edozein kontaketa egin daitekeela ondoriozta daiteke.
Ikus dezagun errekurtsibitatea poligonoen adibidean aplikatzen dela. Horrela, hiruki bat hartuz, behin baino ezin da triangulatu; beraz, a1= 1 lortzen dugu. Gainera, goian ikusi dugun moduan, lauki bat hartuz gero, bi aldiz triangulatu daiteke; hortaz, a2 = 2 lortzen dugu. Orain, pentagonoa hartuko dugu eta haren oinarrian alde bat duen hiruki bat jartzeko hiru modu ezberdin daudela ikus daiteke honako irudian:
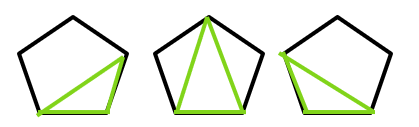
Ezkerreko pentagonoan berdez irudikatutako hirukiak lauki bat du alde batean eta ez du poligonorik bestean. Ohartu laukia, berriz, bi modu ezberdinez triangulatu daitekeela (hots, a2 modu ezberdinetan triangulatu daitekeela). Beraz, ezkerreko irudia a2 bider a0 modu ezberdinez triangulatu daiteke. Erdiko pentagonoaren kasuan, hiruki berdeak hiruki bana du alboetan. Ondorioz, a1 bider a1 modu ezberdinez triangulatu daiteke erdiko pentagonoa. Bukatzeko, eskuineko pentagonoak lauki bat du alde batean eta ez du ezer poligonorik bestean; hortaz, a0 bider a2 modu ezberdinez triangulatu daiteke. Horiek horrela, pentagono bat triangulatzeko modu ezberdin kopurua a2 * a0 + a1 * a1 + a0 * a2 da. Eta a0 = 1 bada, honakoa lortzen dugu 2 * 1 + 1 * 1 + 2 * 1 = 5. Horiek horrela, a3 = 5 argitzea lortu dugu.
Hexagono bat hartuz gero, aurreko arrazoiketa berdina jarraituz, honakoa lortuko dugu: a4 = a3 * a0 + a2 * a1 + a1 * a2 + a0 * a3 . Eta kontuan hartuta orain arte lortu duguna (hau da, a3 = 5, a2 = 2, a1 = 1 eta a0 = 1 betetzen dela), honako emaitza lortzen dugu: a4 = 5 * 1 + 2 * 1 + 1 * 2 + 1 * 5 = 14. Beraz, hexagono bat 14 modu ezberdinetan triangulatu daiteke.
Aurkeztutako metodologiarekin jarraituz gero, an = an-1 * a0 + an-2 * a1 + … + a1 * an-2 + a0 * an-1 dugula frogatu daiteke. Formula errekurtsibo honen bidez, an-1 , an-2 , … a1 eta a0 jakinda, Catalen zenbakien segidaren n elementuaren balioa kalkulatu daiteke. Horrela, n=15 kasurako 9.694.845 balioa lortzen dugu; hau da, Catalanen zenbakien segidaren 15. elementua 9.694.845 da. Edo beste modu batean esanda, 18 albodun poligono bat 9.694.845 modu ezberdinetan triangulatu daiteke.
Egileaz:
Josu Doncel Matematikan doktorea da eta UPV/EHUko Matematika Saileko irakaslea.