Asier Estevan Mugertza
– A,5.
– Joa.
– A,6
– Joa eta hondoratua.
Elkarrizketa hau entzun eta guztioi datorkigu erreza zein arrakastatsua izan den itsasontziak hondoratzearen “Hundir la flota” izeneko mahai-jokoa. Bertan, aurkariek batak besteari planoko koordenatuak adierazten dizkio bertako puntu bat zehaztuz. Irudi bat aski da (x,y) koordenatu bidez planoko puntuak identifikatzeko modu hau ulertzeko:
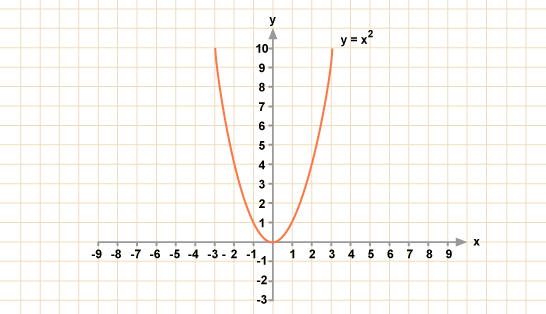
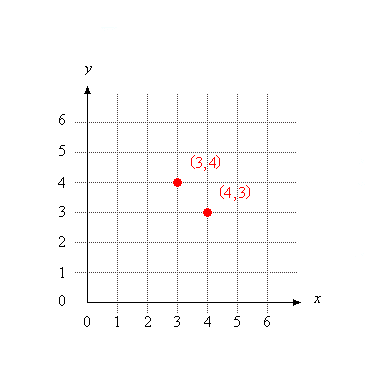 Koordenatuak x eta y aldagaiak bezala definiturik ditugula, euren arteko erlazioak defini ditzakegu. Horrela, bigarren koordenatua y=x² izatea derrigortzen badugu, erlazio hori betetzen duten planoko puntuak (hau da, (x,x²) moduko puntuak) ondokoak izango dira:
Koordenatuak x eta y aldagaiak bezala definiturik ditugula, euren arteko erlazioak defini ditzakegu. Horrela, bigarren koordenatua y=x² izatea derrigortzen badugu, erlazio hori betetzen duten planoko puntuak (hau da, (x,x²) moduko puntuak) ondokoak izango dira:
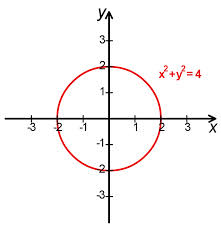
Edota, x²+y²=4 ekuazioa betetzen duten planoko puntuak ere adieraz ditzakegu:
Kasu honetan, Pitagorasen teorema aski zaigu x²+y²=r² ekuazioa betetzen duten planoko puntuek jatorrian (hau da, (0,0) puntuan) zentraturiko r erradioko zirfunferentzia bat osatzen dutela frogatzeko.
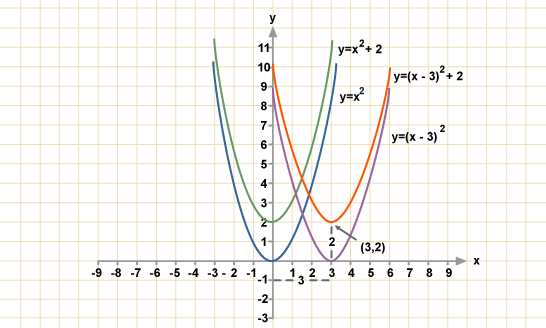
Koordenatuen arteko ekuazio batean “x” beharrean “x-k” idatziz gero (non k konstante bat den), ekuazioari dagokion irudia edo grafika k unitate eskubirantz (hau da, X ardatzean k unitate zentzu positiborantz) mugituko dugu, izan ere, ohartu aldaketa hori egin eta gero, lehen (0,0) puntuak ekuazioan betetzen zuen parera orain (k,0) puntuak betetzen duela. Gauza bera gertatuko da “x”rekin beharrean “y”rekin jolasten badugu. Beraz, dagoeneko badakigu planoko grafikak nola mugitu:
Tira, hau guztia ulertu eta gero, ez da fede askorik behar hiru dimentsiotan, (x,y,z) koordenatuekin gauza bera gertatzen dela sinesteko.
Horrela, adibidez, x²+y²+z²=r² ekuazioa (x²+y²+z²-r²=0 ere idatz dezakegu, noski) betetzen duten espazioko puntuak jatorrian (hau da, (0,0,0) puntuan) zentraturiko r erradioko esferako puntuak dira. Edo beste modu batean esanda, jatorrian zentraturiko r erradioko esferako (x,y,z) puntuek x²+y²+z²-r²=0 ekuazioa betetzen dute.
Edota, planoko r erradiko zirkunferentzia adierazten duen ekuazioaz baliatuz, hiru dimentsiotan x²+y²-r²=0 ekuazioak Z ardatzaren inguruan hedatzen den zilindroa adierazten duela ondoriozta dezakegu.
Esferaren zein zilindroaren r erradioa ekuazioan aldetzeaz gain, espazioan duten posizioa ere alda dezakegu lehen planoaren kasuan ikusi dugun modu berean.
Goazen gaia pixkatxo bat zailtzera…
Demagun orain espazioko bi objetu (Obj1 eta Obj2) ditugula, Ek1=0 eta Ek2=0 moduko ekuazioen bidez adirieraziak, hurrenez hurren. Nola adierazi bi objetu horiek batera? Hau da, zein da bi objetu horiek batera adieraziko dituen ekuzioa?
Bi objetuak batera baditugu, ohartu bertako edozein puntuk Ek1=0 edo Ek2=0 ekuazioa bete beharko duela. Puntua Obj1ean aurkitzen bada, orduan puntuko koordenatuek Ek1=0 ekuazioa beteko dute, eta aldiz puntua Obj2an baldin badago, bere koordenatuek Ek2=0 ekuazioa beteko dute. Ondorioz, putu horiek Ek1*Ek2=0 ekuazioa ere beteko dute hala beharrez. Hau da, Ek3=Ek1*Ek2=0 ekuazio berri honek bi objetu horien puntuak adierazten ditu. Hots, Obj1 zein Obj2ko (x,y,z) puntuek Ek3=Ek1*Ek2=0 ekuazioa beteko dute. Bestalde, espazioko (x,y,z) puntu batek Ek3=Ek1*Ek2=0 ekuazioa betzen badu, orduan Ek1=0 edo Ek2=0 bete beharko du, bietariko bat.
Beraz, dagoeneko badakigu, besteak beste, nola adierazi esfera eta zilindro ezberdinak (erradio eta posizio ezberdinekoak) ekuazio bakar baten bidez:
Demagun orain espazioko bi objetu (Obj1 eta Obj2) ditugula, Ek1=0 eta Ek2=0 moduko ekuazioen bidez adirierazita, hurrenez hurren. Nola adierazi bi objetu horien arteko ebakidura? Hau da, bi objektuk elkar mozten badute, nola adierazi mozketa horren puntuak? Zein da bi objetu horien arteko ebakidura (edo mozketa) adieraziko duen ekuzioa?
Puntu bat bi objektuetan baldin badago, orduan Ek1=0 zein Ek2=0 bete beharko du. Bestalde, eraiki behar dugun ekuazio berrian Ek1=0 eta Ek2=0 ekuazioak betetzen dituzten puntuak baino ezin dira egon. Beste modu batean esanda, bilatzen ari garen ekuazioaren soluzioak Ek1=0 eta Ek2=0 bi ekuazioen soluzio ere izan behar dute.
Hau guztia aintzat hartuz, ohartu bilatzen ari garen ekuazioa ondokoa dela: Ek3=(Ek1)² + (Ek2)²=0
Adibidez, hona hemen erradio bereko bi zilindro perpendikularren mozketa adierazten duen ekuazioa eta irudia: ![]()
Edota r erradioko esfera eta r/2 erradio zilindroa moztean lortzen den Vivianiren kurba, arkitekturan erabilia: ![]()

Agian honez gero urruti gelditu zaigu itsasontziak ondoratzearen mahai jokoa, baina ezagutza minimo hauek aski zaizkigu ondoko espazioko irudiak adierazteko, irudimena lagun dugula noski!
Zomorroa
Armiarma
Lorontzia
Olagarroa:
 Azkenik, ohartu irudiak adierazteko hainbat parametro erabil ditzakegula (a,b,c,…) eta horien balioa aldatuz irudiaren itxura alda dezakegula, animazio bat osatuz fotogramen bidez. Adibidez, gure zomorroaren hanka eta hegoen posizioa eta angelua alda ditzakegu, eta parametro ezberdinei dagozkien fotogramen bidez intsektuaren hegaldia simulatu.
Azkenik, ohartu irudiak adierazteko hainbat parametro erabil ditzakegula (a,b,c,…) eta horien balioa aldatuz irudiaren itxura alda dezakegula, animazio bat osatuz fotogramen bidez. Adibidez, gure zomorroaren hanka eta hegoen posizioa eta angelua alda ditzakegu, eta parametro ezberdinei dagozkien fotogramen bidez intsektuaren hegaldia simulatu.
Egileaz: Asier Estevan Mugertza matematikaria da, eta NUP/UPNAko irakaslea

Sarrera honek #KulturaZientifikoa 1. Jaialdian parte hartzen du.






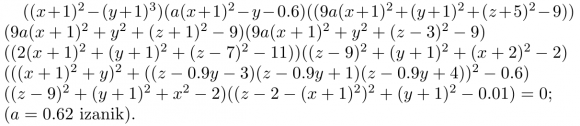
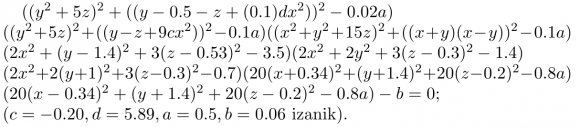


2 iruzkinak
[…] Asier Estevan Mugertza – A,5. – Joa. – A,6 – Joa eta hondoratua. Elkarrizketa hau entzun eta guztioi datorkigu erreza zein arrakastatsua izan den itsasontziak hondoratzearen “Hundir la flota” izeneko mahai-jokoa. Bertan, aurkariek […]
[…] Ag (Z=47): “Irudimena matematizatzen” NUP/UPNAko irakaslea den Asier Estevanek matematikak irudiak eta animazioak egiteko nola […]