Bagatoz berriro ikasketa automatikoaren gaiarekin. Konkretuki, ikasketa gainbegiratuaren bigarren zatiari eutsiko diogu gaurkoan. Gure burmuinak pixka bat martxan jartzeko, gogora dezagun azken sarreran ikasketa gainbegiratua nola gauzatu ikasi genuela aldagai jarraituak ditugunean. Adibide bezala, etxebizitzen prezioak jarri genituen. Ikas al dezake gure ordenagailuak etxebizitzen prezioak aurresaten datu batzuek emanda? Baietz ikusi genuen.
Hala ere, gure egunerokoan badaude beste hainbat arazo ezin direnak aldagai jarraituekin konpondu. Demagun posta elektroniko zerbitzu bat eraiki nahi dugula, Gmail-i konpetentzia egiteko asmoz. Arazoetako bat, jasotako posta spam den ala ez erabakitzea da. Nola egin dezakegu hori? Aldagai diskretuko ikasketa gainbegiratuarekin, noski. Beste benetako adibide batzuk medikuntzan topa ditzakegu: tumore konkretu bat kaltegarria den ala ez, sintoma konkretu batzuekin datorren gaixoak zer gaixotasun duen, eta abar.
Ohartzen bazarete, oraingoan, ordenagailuak ez du balio jarraitu bat ikasi behar, balio diskretu batzuk baizik. Tumorearen kasuan, kaltegarria den (1) ala ez (0), posta elektronikoaren kasuan, spam den (1) ala ez (0), eta horrela beste adibide guztiekin. Arazo mota hauei sailkapen arazoak deritze, azken batean, datu multzo batzuek sailkatu nahi baititugu klase konkretu batzuetan.
Baina zer izango lirateke sarrera hauek betiko grafikorik gabe? Har dezagun tumorean arazoa eta suposa dezagun tumore baten izaera bere tamainarekin erlazionatuta dagoela. Beti bezala, ikaragarrizko sinplifikazioa egin dugu, baina ulertuko duzuen bezala, sinplifikazio horiek egin beharrean gaude grafiko ulergarriak marrazteko.
Ikusten duzuen bezala, tumoreak kaltegarriak (1) ala kaltegabeak (0) izan daitezke. Grafikoan datu batzuk jarri ditugu, laborategian aztertutako tumore batzuen izaera erakusten dutenak beren tamainaren arabera. Datu horiek ikusita, edonork esan dezake badagoela tamaina konkretu bat atari gisa jokatzen duena. Balio hori baino tamaina txikiagoa duten tumoreak ez dira kaltegarriak, baina tamaina handiagokoak bai.
Erregresio logistikoa
Sailkapen arazoak konpontzeko hainbat eta hainbat teknika garatu dira, tartean sare neuronal ospetsuak. Baina oraingo honetan beste teknika bat ikasiko dugu: erregresio logistikoa. Gogoratu zein den sailkapenaren helburua: datu batzuk izanda, eredu bat ikasi nahi dugu datu berriak ongi sailkatzeko.
Hel diezaiogun berriro tumorearen adibideari. Mediku ala biologoren bat hau irakurtzen ari bada, mesedez barka diezadala, baina mundu guztiarentzat ulergarri egiteko adibide bat besterik ez da, hots, errealitatearekin zerikusi gutxi du. Demagun tamainaz gain, orain beste aldagai bat ere badugula tumore baten izaera zehazteko: sustantzia konkretu baten kantitatea. Tamaina x1aldagaia izango da, eta sustantzia horren kantitatea x2. Goazen beste grafiko batekin!
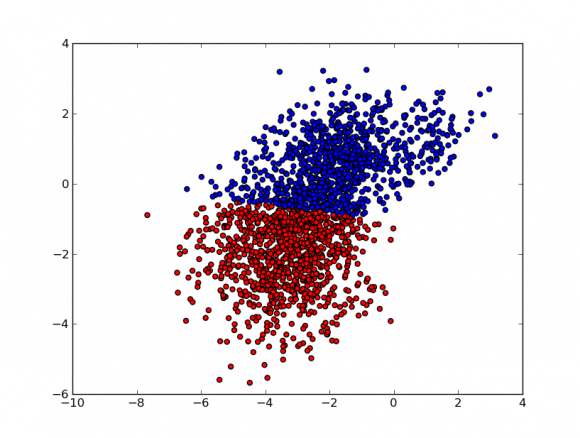
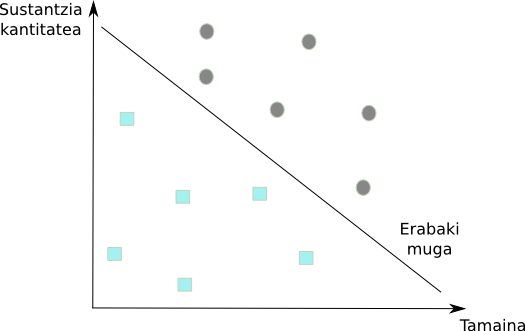
 Bolatxoak tumore kaltegarriak dira eta laukitxoak tumore kaltegabeak. Grafikoari so eginez, argi dakusagu tamaina geroz eta handiagoa den heinean, tumorea kaltegarria izateko aukerak handiagotzen direla. Eta sustantzia kantitatearekin ere antzeko zerbait gertatzen da. Nola bereiz ditzakegu bi tumore klaseak? Zein izango da ikasi behar dugun eredu matematikoa?
Bolatxoak tumore kaltegarriak dira eta laukitxoak tumore kaltegabeak. Grafikoari so eginez, argi dakusagu tamaina geroz eta handiagoa den heinean, tumorea kaltegarria izateko aukerak handiagotzen direla. Eta sustantzia kantitatearekin ere antzeko zerbait gertatzen da. Nola bereiz ditzakegu bi tumore klaseak? Zein izango da ikasi behar dugun eredu matematikoa?
Sailkapen arazoetan erabaki muga izeneko eredu matematiko bat ikasten da. Erabaki mugak bi klaseak bereizten ditu ezaugarrien espazioan – gure kasuan tamaina eta sustantzia kantitateak definituriko espazioan -. Funtzio matematiko bat besterik ez da, zeinak kurba bat ematen digun bi klaseak behar bezala banatzeko. Kurbarik sinpleena, nola ez, zuzena da. Marraz al dezakegu gure adibidearentzako zuzen bat bi klaseak behar bezala bereizteko? Noski baietz!
Marraztu berri dugun zuzen hori ikasi egiten da datuak erabilita. Ikasketa prozesua erregresio linealarena baino zerbait konplexuagoa da, eta beraz ez dugu sakon aztertuko. Ideia ordea sinplea da: ikas dezagun zuzen bat, zeinak bi klaseetako puntuak distantzia berera uzten dituen zuzenetik. Erregresio logistikoak zuzen hori modu honetara interpretatzen du: tumore berri bat badugu, eta bere tamaina eta sustantzia kantitatea ikasi dugun zuzenaren puntu bat bada, tumore hori kaltegarria izateko probabilitatea %50 da. Zuzenaren gainetik badago, zuzenarekiko distantziaren arabera probabilitate hori igo egingo da. Eta alderantziz.
Erabaki muga ez-linealak
Gehienetan, sailkapen arazoak ez dira izaten hain sinpleak. Alde batetik, aldagai edo ezaugarri asko izan ditzakegu, eta bestetik, erabaki mugak ezin dute zuzenak izan, zuzen bat erabilita emaitza oso kaxkarrak lortuko baikenituzke. Ikus dezagun hurrengo grafikoa:
Kasu honetan, inor ez haserretzeko, x1eta x2 aldagaiek ez dute inongo esanahirik. Klase bateko puntuak besteengandik behar bezala bereizteko, zirkunferentzia bat behar dugu, hau da, gure erabaki mugak zirkunferentzia bat izan behar du. Nola egin daiteke hori? Gogoratzen bazarete, zirkunferentziaren ekuazioa x12 + x22 = b da. Ikasterako orduan, aldagaien karratuak erabili beharko ditugu eta horrela, ikasketa prozesuak erabaki muga zirkular bat ikasi ahal izango du. Ez al da polita?
Klase asko ditugunean…
Orain arte ikusi dugunarekin, bi klaseren artean bereizten bakarrik dakigu. Baina zer gertatzen da gure arazoan klase asko badaude? Adibidez, sintoma batzuk emanda, jakin nahi dugu gaixoak gripea duen, malaria ala ebola. Hiru klase ditugu. Kasu horiek konpontzeko badaude hainbat teknika. Sinpleena ondorengoa da: ikasi sailkatzaile bat klase bakoitzarentzako. Sailkatzaile batek ikasiko du sintoma batzuentzako gripea den ala ez. Beste batek malaria den ala ez. Eta azken batek ebola den ala ez. Sintoma konkretu batzuekin datorren gaixo betentzako, sintomak jarriko ditugu lehen sailkatzailean; gripea ez bada, hurrengo sailkatzailera joango gara: malaria dela esaten badigu, jada jakingo dugu gaixoak malaria duela eta ez beste edozein gaixotasun.
Bizitza errealean konpondu beharreko arazoak hemen ikusi ditugunak baino konplexuagoak izan ohi dira:
- Ezaugarri asko egon daitezke klase ezberdinak bereizterako orduan. Ezaugarri askok aldagai asko ekartzen ditu eta beraz, gure espazioak dimentsio handikoak izan ohi dira. Puntuak eta beraien arteko erlazioak hainbeste dimentsiotako espazioetan irudikatzea ez da posible izaten eta beraz, arazoa ulertzea askoz zailagoa da.
- Ezaugarri egokiak aukeratzea ere ez da lan erraza izaten. Analisi asko egin behar izaten dira ezaugarri garrantzitsuenak identifikatzeko.
- Erabaki mugaren itxura ezin da jakin aldez aurretik. Guk jarri ditugun adibideetan espazio oso sinpleak ikusi ditugu. Ikuste hutsarekin bagenekin nolako erabaki muga behar genuen. Baina dimentsio pilo bat ditugunean, ezin dugu jakin nolako erabaki muga behar dugun. Ordenagailuak berak ikasi beharko du. Horretarako, ezaugarriak behin identifikatzen direnean, ezaugarri horien karratuak, kuboak eta abar ere sartzen dira ikasketa prozesuan. Askotan ezaugarri multzo ezberdinekin emaitzak ikusten dira eta onenekin geratu.
Amaitzeko
Ikasketa gainbegiratuaren bi arazo nagusiak aztertu ditugu jada. Gogoratu ikasketa gainbegiratua ikasketa automatikoaren arlo bat dela. Ideia ordenagailu bati adibide batzuk ematea da, hark eredu bat ikas dezan eta datu berriak behar bezala sailkatzeko gai izan dadin. Ikasketa gainbegiratua gaur egun arazo pilo bat konpontzeko erabiltzen da: diagnostiko medikoetan laguntzeko, erresonantzia magnetikoak aztertzeko, teleskopioetako irudietan galaxiak, izarrak eta bestelako egiturak bereizteko, ikusmen artifizialean objektuak sailkatzeko eta abar luze bat. Zeharo garrantzitsua bihurtu da. Espero dut sarrera hauekin ulertuko dela zertarako balio dezakeen ikasketa gainbegiratuak eta zein diren bere oinarri matematikoak.
Egileaz: Gorka Azkune (@gazkune) informatikaria da eta DeustoTech-eko ikertzailea.


2 iruzkinak
[…] dago oinarrituta (aurreprogramatutako paketetan, software librekoak askotan), eta datuak dira gakoa [5]. Adibidez, gaixotasun baten detekzioa egiteko espediente medikuetako informazioa biltzen da, […]
[…] oinarrituta (aurreprogramatutako paketetan, software librekoak askotan), eta datuak dira gakoa [5]. Adibidez, gaixotasun baten detekzioa egiteko espediente medikuetako informazioa biltzen da, […]