Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta aurten ere, udako oporretan egiteko asteazkenero ariketa matematiko bat izango duzu, Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.
Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.
Hona hemen gure laugarren ariketa: zein da zirkulu txikiaren azalera?
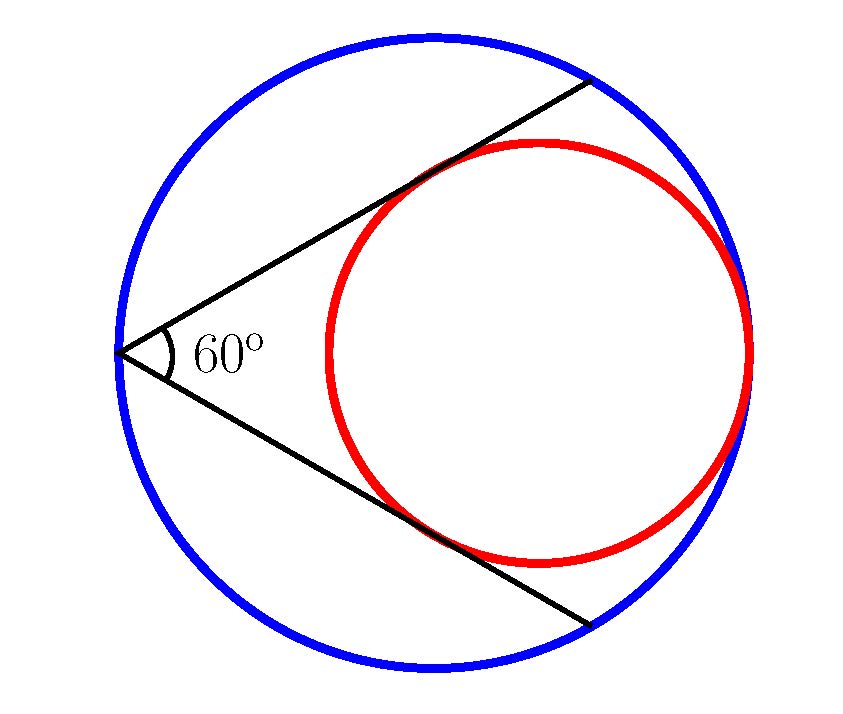
4) Zirkulu handiaren azalera 9 cm2 da. Zein da zirkulu txikiarena?
Ariketak Frantziako CNRSren blogeko Défis du Calendrier Mathématique ataletik daude hartuta.
7 iruzkinak
4
Neri zirkulo txikiaren area 4cm2 ateratzen zait.
Zaila zait garapena idaztea irudirik ipini gabe, baina saiatuko naiz.
1) Zirkulu handiaren erradioa; 9=πR2, nondik R=9/√π
Deitu dut x angeluaren etzea zirkunferentziarekin bat egiten duen puntua eta barriko zirkunferentziaren erdia batzen duen sektorea eta r zirkunferentiza honen erradioari,
(berez, x+r=2R) (1)
Deitu diot a zirkulu txikia eta angeluko marrak bat egiten duten puntuari (non marra hau r erradioarekiko tangentea da)
orduan honako hau ezarri dut
x(0)+r(120)+a(210)=0
nun parentesi arteko zenbakiak angeluak (gradu sexagesimeletan diren)
honela;
xCos(0)+rCos(120)+aCos(210)=0
xSen(0)+rSen(120)+aSen(210)=0
non Cos(0)=1, Cos(120)=-1/2, Cos(210)=-(√3)/2,
eta Sen(0)=0, Sen(120)=(√π)/2, eta Sen(210)=-1/2
valoreak ipiniz eta despejatu ondoren ateratzen zait;
x=2r
(1) ekuazioan baloreak ordezkatuz 2r+r=6/√π, berez r=2/√π. r2=4/π a=π*4/π=4
zirkulu txikiaren area 4 Cm2 ateratzen zait.
¿Zuzena al da?
Bai, nire ustez zuzena eta dotorea zen erabat intuitiboa.
Horri buruz gehiago edo gutxiago:
3 tangentziarrek triangelu bat osatzen dute alde berdinetan.
Simetriaren arabera, alde horietako bat zirkunferentzia handiagoaren erdian igarotzen da.
Lerro tangenteen perpendikularra den bi erradiok triangeluaren triangeluaren eremuaren hirugarren zatia osatzen duten triangeluak osatzen dute.
Zirkulu txikiagoaren erradioa eta triangelu horren altuera zirkunferentzia handiagoaren erradioaren berdina da.
Triangeluen eremuetatik 1etik 3ra bitarteko erradioaren arabera, erradio txikiagoak erradio handiagoaren bi herenak dira.
9 = π. (3 / 2.r) 2 = π. 9/4. r2, eta gero π.r2 = 4
Milaka itzulpengintzako apologiak, baina euskaraz ez da ohikoa nire herrialdean, nahiz eta pare bat leku irakatsi.
Kaixo, Luis,
Eskerrik asko parte hartzeagatik eta erantzuna eta honen azalpena bidaltzeagatik!
Bi aste barru ezagutuko ditugu emaitza zuzenean Javi Duoandikoetxea matematikariaren eskutik.
Mila esker eta laster arte!
Oso erantzun elegantea iruditzen zait zurea.
Kaixo, Iñaki,
Eskerrik asko emaitza eta honen azalpena emateagatik!
Zuzena den edo ez jakiteko egun batzuk itxaron beharko ditugu. Irailaren erdialdean emango ditu ezagutzera emaitza zuzenak Javi Duoandikoetxea matematikariak.
Mila esker eta laster arte!
Eskerrik asko Luis! Zientzia Kaiera blogean ere argitaratu dugu zure emaitza. Mila esker parte hartzeagatik.