Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta aurten ere, udako oporretan egiteko astelehenero ariketa matematiko bat izango duzu, Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.
Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain, tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.
Hona hemen gure hirugarren ariketa: Erradioaren bila.
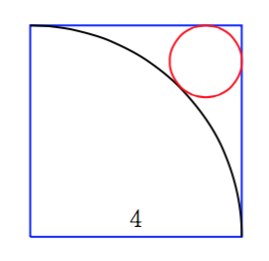
3) Karratu baten aldeak 4 cm ditu. Zirkunferentzia laurden bat inskribatu dugu karratuan eta gero zirkunferentzia txiki bat egin dugu, karratuaren alde biren eta zirkunferentzia laurdenaren ukitzailea, irudiak erakusten duen moduan. Zein da zirkunferentzia txikiaren erradioa?
Ariketak “Calendrier Mathématique 2019. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.
4 iruzkinak
Emaitza 0.58579
Karratu handiaren diagonala atera (pitagoras) eta zirkunferentzia laurdenaren erradioa kenduz karratu txiki berri baten diagonala dugu (barruan zirkunferentzia txikia duena). Datu horrekin zirkunferentziaren diametroa atera (berriro pitagoras, alderantziz) eta zati bi erradioa lortu duzu.
Hainbat buelta eman dizkiot, diagonala, karratu ezberdinak eta pitagoras erabilita, baina ez dut asetzen nauen hurbilketarik lortu. Asike ebazpenera itxarongo dut!
Ariketa erreza zirudien, baina bakarrik itxura zen.
Problema honen berri izan nuenean kanpoan nengoen eta aste bukaera iritxi arte ezin izan diot serioski buelta bat eman. Itxuraz erreza zirudiena, korapilotsu bihurtu da eta zaila iruditu zait.
Ezin dut iruzkin honetan irudirik atxiki, honek ere azalpena zaildu egiten du.
Imagina dezagun diagonal bat. Honen neurria 4V2=5.6568cm koa da. Zirkunferentzitik laukiaren arteko distantzia 5.6568-4=5.6568=1.6568 cm koa da, honen barruan kokatzen da bere erradioa ebatzi nahi dugun zirkunferentzia. Deitzen ba dugu a eta b zirkunferentzia honek laukiarekin dituen bi interseksio puntuak eta c bi zirkunferentziaren elkarreko intersekzio puntua eta azkenik d laukiaren ertzea, acbd r neurria duen lauki bat osatzen dute, bere diagonala rV2 izanik. Honela begiratuta zirkunferentziatik laukiaren arteko distantzia r+rV2 da, zenbakitan 1.6568=r+rV2, r=1.6568/(1+V2)=0.6862cm, hankarik sartu ez badut.
Problema hau ezagutzen nuen beste formato batean, bigarren hezkuntzako oposizoetan jarritakoa, baina bietan funtsezko emaitza, erradioen arteko erlazioa, berdina. Iñakirekin bat nator, erraza dirudi, baina kosta egiten da erradioen arteko erlazioaz konturatzea, irudi on bat laukidun orri batean egiten bada errazago ikusten da.
Uste dut Iñakik primeran ebatzi duela.
Honako loturan aipatutako problema uzten
dut:
https://sites.google.com/site/egingodugumate/ope/2-problema
Problema polita benetan, asmatu ala ez asmatu, buruan buelta batzuk ematea merezi duen horietakoa.