Javier Duoandikoetxea

Bizitzen ari garen aro berezi honetan, askotan aipatu digute zientziaren balioa eta beharra. Matematikak ere bere ekarpena egiten du, epidemien bilakaera aurreikusteko tresnak eskura jartzen baitizkigu, besteak beste. Horretarako proposatu ziren lehen eredu matematikoek laster beteko dute mendeurrena.

Eredu matematikoak

Eredu matematiko batek tresna matematikoak erabiltzen ditu bizitza errealeko fenomeno bat era abstraktu eta sinplifikatuan aztertzeko. Horretarako, fenomenoan agertzen diren magnitudeen arteko erlazioak formulazio matematiko baten bidez azaldu behar dira.

Eredu matematikoen erabilera eta arrakasta desberdina da zientzia batzuetan eta besteetan. Bistan da fisika oso matematizatuta dagoela, baina bizitzaren zientzien kasuan, aldiz, ez da izan hain agerikoa matematikaren presentzia. Batzuen ustez, biziari loturiko guztia konplexuegia da matematikaren eredu sinple eta abstraktuetara egokitzeko. Diotenez, matematika aplikatuaren XXI. mendeko erronketako bat horixe izango da: matematikaren erabilera handitzea biziaren zientzietan.

Hori esanda ere, aspaldi hasi ziren proposatzen zenbait eredu matematiko biologian, eta aurrerapen handiak egin dira azken aldian arlo horretan. Gaixotasun infekziosoetarako ereduak, esaterako, ez dira oraingoak eta hemen aipagai izango dugunak laster beteko ditu 100 urte: A Contribution to the Mathematical Theory of Epidemics artikulua 1927an plazaratu zen. William Ogilvy Kermack eta Anderson Gray McKendrick ziren egileak.

SIR eredua

Izakien populazio bateko kideak hiru multzotan sailkatzen dira: kutsagaiak (S=susceptible), kutsatuak (I=infected) eta kutsaezinak (R=recovered). Kide bakoitza une bakoitzean talde horietako bakar batean dago. Baina batetik bestera igaro daiteke, norabide bakarrean, eskema honek erakusten duen moduan:

S → I → R

Beraz, kutsagai bat kutsatu daiteke (S-tik I-ra pasatuko da) eta kutsatu bat senda daiteke edo hil (I-tik R-ra pasatuko da). Eredu horretan onartzen da immunitatea lortzen dela sendatu ondoren, eta ez dela berriro S-ra itzultzen.

Gaixotasunak hiltzen dituenak ere R multzoan sartu ditugunez, populazioa konstante mantentzen da orotara. Irakurlea konturatuko da ereduak sinplifikazio bat egiten duela, ez baititu kontuan hartzen jaiotzak, ez eta infekzioaz bestelako arrazoi bategatik hildakoak. Badaude kasu horiek ere kontuan izaten dituzten eredu konplexuagoak.

Ekuazioak

Izan bedi t denbora adierazten duen aldagaia eta S(t), I(t) eta R(t) multzo bakoitzean t unean dagoen kide kopurua. Aipatu ditugun arrazoiengatik, horien batura konstantea da. Izan bedi N populazioaren tamaina, hau da, S(t) + I(t) + R(t) = N da, t guztietarako. Ekuazioak idazteko, hiru funtzio horien aldaketaren abiadura formulatu behar da. Abiaduraren adierazpen matematikoa deribatua da.

Hauek dira SIR ereduaren ekuazioak:

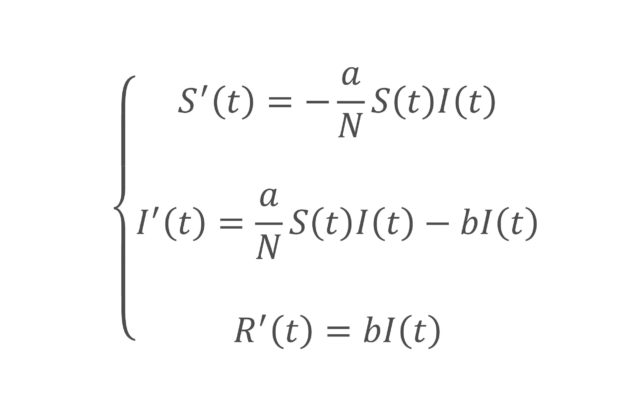
Kutsagaiak eta kutsatuak elkartzen direnean, S taldeko batzuk kutsatu egingo dira. Kutsatzeko arriskua S eta I taldekoen elkartzeen araberakoa denez, SIR ereduaren hipotesia da haien topaketak S eta I-ren biderkaduraren proportzionalak direla. Eta bada faktore bat, transmisio-tasa, horrekin biderkatu behar dena, kutsagaien aldaketaren abiadura emateko. Tasa hori a/N idatziko dugu, eta horregatik agertzen da ekuazioetan gaia, horrek adierazten baitu S-tik I-ra igarotzeko abiadura. Prozesuan kutsagaiak gutxitu eta kutsatuak handitzen direnez, S’-rako negatiboa da eta I’-rako, berriz, positiboa.

Beste alde batetik, I-tik R-ra joango dira sendatu edo hiltzen direnak. Zenbat doazen neurtzeko, berreskuratze-tasa bat dugu eta hori kutsatu kopuruarekin biderkatu behar da. Horregatik dugu gaia ekuazioetan; negatiboa da I’-rako, kutsatuak gutxitzen dituelako, eta positiboa R’-rako, kutsaezinak handitzen dituelako.

Ekuazioak ebatzi ahal izateko, hasierako datuak behar dira, hau da, t = 0 unean talde bakoitzean dagoen kide kopurua. Pentsa dezakegu hasieran I(0) = 1 dela (zero pazientea), baina bat baino gehiago ere izan daiteke. Gainera, S(0) > 0 izango da, kutsagaiak behar baititugu infekzioa heda dadin.

Ekuazioen soluzioak

Ez dago ekuazioen soluzio zehatza kalkulatzerik. Hori, ordea, ez da arazoa, ordenagailuz soluzio hurbilduak eman baitaitezke. Baina ekuazio-sistema ebatzi barik ere, soluzioen zenbait propietate kualitatibo lortzeko tresnak ditu matematikak.

Horrela, ikusten da soluzioen portaera a/b zenbakiaren araberakoa dela. Hori da R₀ zenbakia edo oinarrizko birsorkuntza-tasa, kasu honetan. Baldin R₀ > 1 bada, infekzioa hedatzen hasiko da, eta R₀ < 1 bada, aldiz, ez. Dena dela, oinarrizko balio horrek hasieran eragina badu ere, aurrerago hobe da birsorkuntza eraginkorraren tasa erabiltzea, aS(t)/Nb. Hasierako S(0) eta N ia berdinak direnez, R₀-ren ia berdina da t = 0 denean, baina gero txikituz doa S-rekin batera.

Ekuazio formalak idaztea erraza den arren, arazo bat da hor sartu behar diren a eta b parametroen balioak ondo aukeratzea. Bigarrena, nolabait, gaixoek berreskuratzeko zenbat denbora behar duten aztertuta erabaki daiteke. Aitzitik, a-ren balioa ematea zailagoa da. Hutsetik abiatzen bagara, balio hori ezezaguna da eta behatu behar da zein den hasierako kutsatze-erritmoa. Batzuetan, beste lurralde bateko datuak edo beste garai batekoak erabiltzen dira, baina horiek informazio okerra eman dezakete. Gainera, eredu sinplifikatu honek a eta b konstante mantentzen ditu denboran zehar, baina praktikan neurriak har daitezke balio horiek aldatzeko.

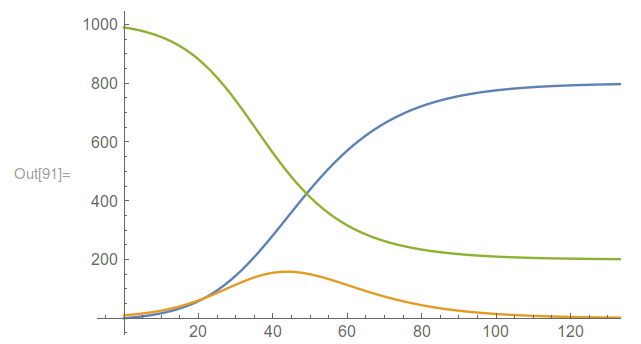
Edozein kasutan, ekuazioen ondorio bat da I(t) balioak 0-rantz jotzen duela denbora handitu ahala, hau da, kutsatuak desagertu egiten direla. Hain zuzen ere, ekuazioen azterketak erakusten du infekzioa hedatzeko atalase-balio bat dagoela. Kutsagaien kopurua balio horretatik behera badago, infekzioa ez da zabaltzen. Beraz, kutsatuak desagertuko dira, nahiz eta kutsagaiak geratu. Datu errealekin ez da ikusten atalase bat dagoenik, eta eredu matematikoa funtsezkoa izan zen halako ondorio batera heltzeko.

Beste alde batetik, I(t) funtzioa balio maximo batera heltzen da eta gero beherantz hasten da, berriro igo barik. Hau da, piko bakarra du. Berriro ere eredu matematikoak erakusten duen propietate bat da. Hala ere, kontuan izan eredua oso sinplea dela eta batzuetan errealitatea desberdina izan daitekeela.

Esku-hartze publikoa

Ereduak erakusten du infekzioaren hedapena moteldu daitekeela, birsorkuntza eraginkorraren tasaren gainean eraginda. Birusetarako, ekintza hauek aipa ditzakegu:

• Gutxitu gaixotasun-denbora botikekin.
• Gutxitu kutsagaiek kutsatuekin izan ditzaketen harremanak, isolamendu-neurrien bidez.
• Gutxitu transmisio-probabilitatea eskuak askotan garbituz eta maskarak erabiliz.
• Gutxitu hasierako S(0) balioa txertoen bitartez.

Ezagunak egiten zaizkigu, ezta? Irakurleak pentsa dezake Covid-19 gogoan idatzitako aholkuak direla horiek. Bada ez, 2013ko dibulgazio-artikulu batetik hartu ditut eta gripeaz ari da egilea. Ekuazio matematikoen soluzioen bilakaera du gogoan, birsorkuntza eraginkorraren tasa jaisteko moduak baitira a eta S(t) gutxitzea eta b handitzea.

Txertoen eragina

Aurreko aholkuen artean zegoen txertoen aukera ere. Horrek hasierako kutsagaien kopurua gutxitzen du eta birsorkuntza eraginkorraren tasa a(1-p)/b bihurtzen du, non p den txertatuta dagoen populazio totalaren frakzioa, txertoaren eraginkortasuna ere kontuan hartuta. Adibidez, populazioaren % 70 txertatuta badago eta txertoak % 90eko eraginkortasuna badu, p = 0.63 izango da. Ezin izaten da populazio osoa txertatu eta, gainera, eraginkortasuna ez da % 100 izaten, beraz, p < 1 da.

Hortaz, a eta b parametroen balioen arabera, kalkula daiteke populazioaren zer proportzio txertatu behar den infekzioaren hedapena ekiditeko (edo asko apaltzeko). Helburua da kutsagaien kopurua lehen aipatu dugun atalase-baliotik behera egotea hasieratik. Hori eginez gero, talde-immunitatea lortu dela esaten da. Txertatu barik daudenentzat ere onuragarria da talde-immunitatea, eta horrek mesede egiten die txertoen aurka daudenei, noski. Aitzitik, populazioaren zati handi bat txertoen aurka badago, talde-immunitatea hasieratik lortzeko aukera galtzen da.

Beste eredu batzuk

“Eredu guztiak oker daude, baina batzuk erabilgarriak dira”, zioen George Box estatistikari britainiarrak. Errealitatea hainbeste sinplifikatzen denez, beti egongo da aldea matematikak aurresaten duenaren eta benetan gertatzen denaren artean. Garrantzitsuena, hala ere, Boxek aipatzen duen erabilgarritasuna da. Lan batzuek erakutsi dute SIR eredua, bere sinpletasunean, ondo egokitzen zaiela gertaturiko zenbait epidemiari. Hala ere, gertatu eta gero errazagoa izan daiteke egokitzapena, ekuazioen parametroak hobeto kontrolatzen direlako.

Dena dela, SIR eredua ez da bakarra, eta bertsio garatuagoetara jotzen da batzuetan. Talde gehiago sartu barik, aldaera hauek aipa ditzakegu:

• Dinamika bitala kontuan hartzea: jaioberriak S taldean sartzen dira; infekzioa ez den beste arrazoiengatik hildakoak gertatzen dira talde guztietan.
• SIS eredua: ez dago immunitaterik. Kutsatuak sendatu eta gero, berriro S taldera doaz.
• SIRS eredua: immunitatea denbora baterako da. R-tik berriro S-ra igarotzen dira, baina ez berehala.

Beste eredu batzuetan talde berri bat edo gehiago agertzen dira. Zehazki, hauek har daitezke kontuan:

• E (exposed): inkubazio-aldian dauden kideak. Kutsatuta daude, baina oraindik ez dute infekzioa transmititzen.
• M (maternally derived immunity): jaioberriak immuneak dira denbora baterako, amaren antigorputzei esker.
• D (deceased): infekzioak hildakoak. Hauek R taldetik ateratzen dira; R-n bakarrik geratzen dira gaixotasunetik bizirik irten direnak.

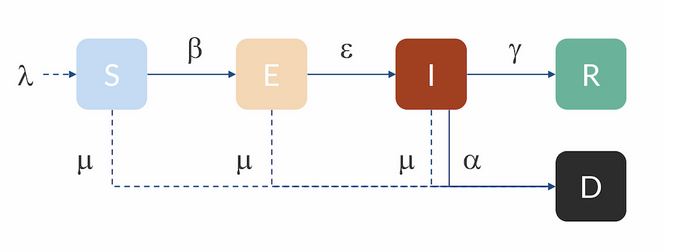
Horiek kontuan hartuta, era honetako ereduak proposatu dira: SEIR, SEIS, MSIR, SIRD, SEIRD, MSEIR, MSEIRS… Ereduen izenek argi erakusten dute bakoitzean zer talde sartzen diren eta zein diren talde batetik bestera igarotzeko bideak. Ekuazio gehiago eta beste zenbait parametro behar dira, noski.

Gehiago jakiteko:

Informazio ugari aurki daiteke sarean gaiari buruz. Hona hemen zenbait iturri:

1. Compartmental models in epidemiology artikulua ingelesezko Wikipedian.
2. Weiss, Howard (2013). The SIR model and the Foundations of Public Health. Materials matemàtics, 2013 (0), 1-17.
3. Hethcote, Herbert W. (2000). The mathematics of infectious diseases. SIAM Review, 42 (4), 599-653.
4. Ridenhour, Benjamin, Kowalik, Jessica M. eta Shay, David K. (2018). El número reproductivo básico (R₀): consideraciones para su aplicación en la salud pública. American Journal of Public Health, 108 (S6), S455_S465. DOI: https://doi.org/10.2105/AJPH.2013.301704s
5. Covid-19 gai duen artikulu bat: Ed Fontes, Modeling the Spread of COVID-19 with COMSOL Multiphysics, COMSOL blog, 2020-04-07.

---

Egileaz:

Javier Duoandikoetxea Analisi Matematikoko Katedraduna da UPV/EHUn.