Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta aurten ere, udako oporretan egiteko asteazkenero ariketa matematiko bat izango duzue, Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.
Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain, tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.
Hona hemen gure bosgarren ariketa: Perimetroaren bila.
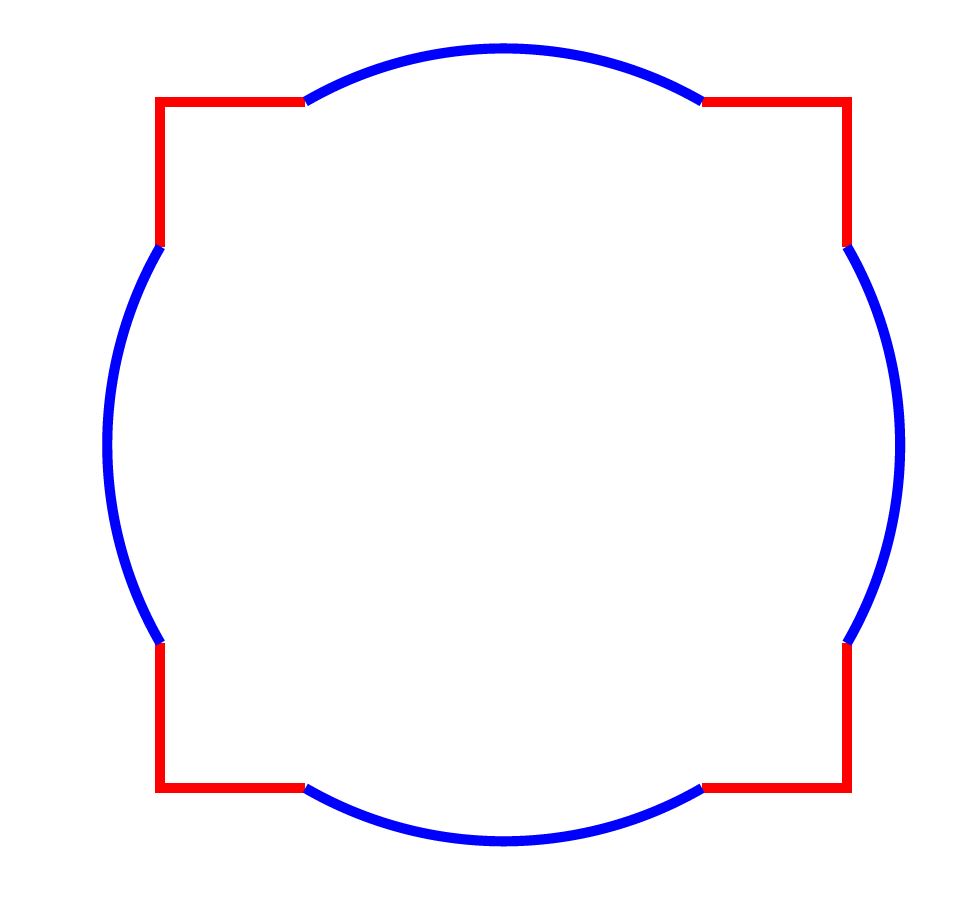
Goiko irudia egiteko √12 zentimetroko aldea duen karratu bat 2 zentimetroko erradioa duen zirkulu baten gainean ezarri dugu, biak zentro bera izanik. Zein da irudiaren perimetroa?
Ariketak “Calendrier Mathématique 2021. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.
Utzi zuen erantzuna iruzkinetan!
2 iruzkinak
14,23 zentimetro
laukia eta zirkulua 30º eta 60º-etan elkartzen dira. Beraz:
kurba urdiñek: zirkunferentziaren bi heren: 4*pi*r/3
zuzen gorriek: 8 dira, eta bakoitzak (√12/2-2sin(30º))
Gabon;
Neri ateratzen zait perimetro bezala 14.2339 cm.
Irudika dezaket lau laukitxo non guzti hauen erpin bat figuraren erdian daukaten. Lauki hauen alde batek V12/2=V3=1.73205 cm ko neurria daukat.
Irudiaren zentroa eta alde baten erdia lotzen duen marra bertikalak V12/2=V3=1.73205 cm neurtzen du.
Irudika dezaket hiruki rektangulo bat. Non hipotenusak 2 eta alde batek V3 balio duen. Pitagoras erabilita falta zaidan aldea 1 balio du. Hipotenusa eta V3 balio duen arteko angelua 30º koa da.
Baldin eta zirkunferentziaren perimetro osoa 2*2*Pi bada hiruko erregela erabiliz
360º—->2*2*pi
030º—->1.04719
Beste alde batetik laukiaren diagonala (V6) erradioa (2) baina luzego denez zirkulotik kanpo dagoen laukiaren aldea izango da l=V3-1=0.73205cm
Bi perimetroen luzera =0.73205+1.04719=1.77924
Hau da perimetro osoaren zortziren bat, berez P=1.77924*8=14.2339cm.