Sinpletasunaren iragarrezintasuna: automata zelularrak
Gutxik aurreikusi zuten —horien artean, John von Neumann matematikari hungariarrak— zientziaren hurrengo gidoi aldaketa handia ez zela «energia, lana, indarra edo mugimenduaren» esparruetan gertatuko, aurrekoetan bezala, baizik eta «kontrol, programazio, informazioaren prozesamendu, komunikazio, antolakuntza eta sistemen» esparruan (Burks, 1969). Bigarren Mundu Gerraren ostean lehenengo konputagailuak sortu ziren; hau da, gure zeregin mentalekin (ez fisikoekin) laguntzeko lehen makina sofistikatuak. Eta, horrekin batera, bizitza artifizialki birsortzeko aukera errealista jarri zen mahaiaren gainean. Halaxe jaio zen zibernetika. Norbert Wienerrek proposatu zuen XX. mendearen berrogeiko hamarkadan, eta halaxe sortu ziren lehendabiziko eredu konputazionalak. Horien helburua zen naturan soilik aurki zitezkeen prozesuak simulatzea eragiketa logikoen bidez.
Konrad Zuse ingeniari alemaniar eta konputazio modernoko aitzindariak problemarako hurbilketaren bat egin zuen. Eta ordutik gutxira, Los Alamosko Laborategi Nazionalean, aurrera egin zuten gaian. Alde batetik, John Von Neumannek planteatu zuen sistema konputazional batek bere burua modu autonomoan erreplikatu ahal izateko aukera; eta, bestetik, Stanislaw Ulamek jakin nahi izan zuen ea arau matematiko sinpleetatik abiatuta egitura, patroi edo jokabide konplexuak sor zitezkeen. Ulamek dimentsio biko saretak erabili zituen horretarako, zeinetan datuak adierazteko gelaxkak markatzen zituen —edo ez—. Von Neumannek Ulamen metodoa erabili zuen bere sistema autorreplikatzaileetako bat sortzeko. Hala ere, ezagutzen dugun lehenengo automata zelularra izan bazen ere, eredu hori ez zen batere nabarmendu, eta hamarkadatan ahaztuta geratu zen.

Hirurogeita hamarreko hamarkadan, Scientific Americanen aisialdiko matematikaren atalean, Martin Gardnerrek jolas gisa planteatu zuen ideia sinple baina zoragarri bat, John Conway matematikari ingelesak izandakoa. «Bizitzaren jolasa» zuen izena, organismo populazioen bilakaera dinamikekin zuen antzekotasunagatik, eta arau oso sinpleak zituen.
Bizitzaren jolasean aritzeko lauki-sare bat besterik ez da behar, zeinetan gelaxkak marka daitezkeen; adibidez, xake edo go ohol bat, pieza batzuk, papera, arkatza… baina errazena eta argigarriena, egun, ordenagailu bat erabiltzea da. Markatutako gelaxkak gure Sareta Munduan modu erabat autonomoan eboluzionarazi ditzakegun organismo edo zelulen baliokideak izango dira, hasierako konfigurazio geometriko batetik abiatuta, soilik arau hauek behin eta berriro aplikatzearen bidez:
- Bizirautea: inguruan bi edo hiru zelula dituen zelulak hurrengo belaunaldian biziraungo du.
- Hiltzea:
- Inguruan lau zelula edo gehiago dituen zelula hil egingo da, superpopulazioaren ondorioz.
- Inguruan zelula bat edo bat ere ez duen zelula hil egingo da, isolamenduaren ondorioz.
- Jaiotzea: gelaxka huts baten inguruan hiru zelula baldin badaude, hurrengo belaunaldian zelula berri bat jaioko da gelaxka horretan.
Eta kito. Jolasa «bera bakarrik jolasten da». Guk zelulen hasierako konfigurazioa besterik ez dugu erabaki behar.
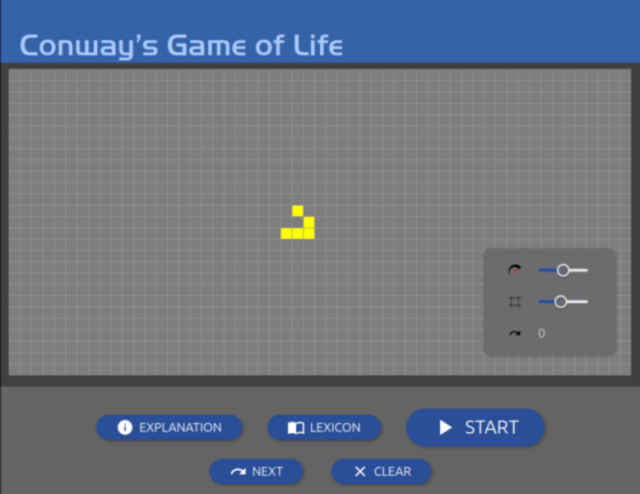
Von Neumannek planteatutako eredua bezala, bizitzaren jolasa automata zelular bat da, baina pixka bat sinpleagoa. Ideia hori jendartean zabaldu zen dibulgazio zientifikoko aldizkari batean argitaratu zenean. Orduan, matematikariak nahiz afizionatuak hasierako konfigurazio anitzekin esperimentatzen hasi ziren, eta fenomeno oso interesgarriak deskubritu zituzten: patroi egonkorrak —belaunaldiz belaunaldi aldatzen ez direnak—, errepikatzen diren zikloak, figurak —«planeagailuak»—, saretatik igarotzen direnak mugimendu sentsazioa agerraraziz, bai eta beren burua autorreplikatzen duten egiturak ere. Interneten, jolas sinple horren bidez sortutako aparteko artelan geometrikoak aurki daitezke —Pazko arrautza: bilatu Googlen «bizitzaren jolasa»—.

Von Neumman, Ulam eta Conwayren lanetatik abiatuta, laurogeiko hamarkadan, Stephen Wolfram fisikaria automata zelular horiek ikertzen hasi zen. Kasu horretan, automata dimentsiobakarrak hartu zituen aztergai —gelaxken ilara bakar bat dira eta «elemental» gisa dira ezagunak—, eta horien jokabidea aintzat hartuta, konplexutasunaren arabera sailkatu zituen; honela:
- 1. klasea: egoera egonkorretara iristen dira.
- 2. klasea: patroi oszilatorioak edo periodikoak sortzen dituzte.
- 3. klasea: patroi pseudoausazkaoak edo kaotikoak sortzen dituzte.
- 4. klasea: egitura konplexu baina ordenatuak sortzen dituzte.

Beste behin ere, agerian geratu zen sareta batean oso sinplea den arau sistema bat aplikatuta patroi konplexuak lor daitezkeela. Hori guztia kontuan hartuta, Wolframek automata zelularren teoria aplikatu zuen, gero eta modu osatuagoan, fisikaren esparruan, eta planteatu zuen agian unibertsoa horrelako eredu konputazional baten bidez deskriba litekeela… Baina, antzeko kasuetan bezala, horrek eztabaida piztu zuen fisikaren munduan.
Automata zelularrak jolas gisa hartzeaz edo egiazko eremuetan aplikagarriak direla uste izateaz harago, ezin da ukatu sorpresa matematikoen iturri direla. Horien potentzialak eta, seguruena, baita edertasunak ere, Greg Egan zientzia fikziozko idazlea inspiratu zuten 1994. urtean Permutation City nobela idazteko; lan hori matematikaren, konputazioaren eta bizitzaren omenaldi itzela da.

Egileaz:
Gisela Baños zientzia, teknologia eta zientzia fikzioaren dibulgatzailea da.
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2025eko urtarrilaren 9an: La impredecibilidad de la sencillez: autómatas celulares.
Itzulpena: UPV/EHUko Euskara Zerbitzua.