Dozena erdi ariketa 2021eko udarako: erantzunak
Javier Duoandikoetxea
Kantitate bat ordaindu ahal bada, horri 5en multiploak gehituta lortzen diren guztiak ere ordaindu ahal dira. Horretan oinarrituta, 5ekiko zatiketek uzten duten hondarraren arabera antolatuko ditugu zenbakiak.
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | |
| 1 | 6 | 11 | 16 | 21 | 26 | 31 | 36 |
| 2 | 7 | 12 | 17 | 22 | 27 | 32 | 37 |
| 3 | 8 | 13 | 18 | 23 | 28 | 33 | 38 |
| 4 | 9 | 14 | 19 | 24 | 29 | 34 | 39 |
Lerro bakoitzean gorriz daudenak ezin dira lortu 5eko eta 7ko txanponak erabiliz. Lehen lerroko guztiak 5eko txanponekin lortzen dira. Beste lerroetan, lehen zenbaki beltza 7ko txanponekin lortzen da eta besteak 5ekoak gehituta. Ordaindu ezin den kantitate handiena 23 da, beraz.
Joseluren eta Koldoren erantzunak zuzenak dira. Joselurena ederto azalduta, gainera.
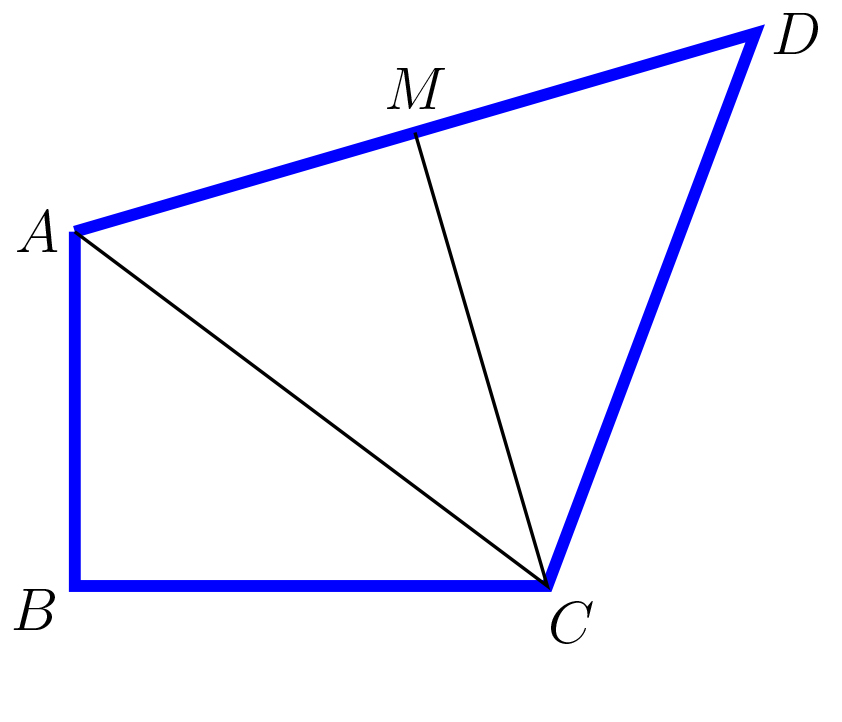
ABC triangelua zuzena denez, Pitagorasen teorematik AC = 5 cm ateratzen dugu. Orduan, ACD triangelua isoszelea da eta CM altuerak bi triangelu zuzen berdinetan zatitzen du. AM = MD = 3 cm denez, hiru triangelu zuzen berdin ditugu. Bakoitzaren azalera (3 x 4) : 2 = 6 cm2 da. Hortaz, laukiaren azalera 18 cm2 izango da.
Iñakik, Estik, Koldok eta Joseluk zuzen eman dute 18 balioa. Batzuek 18 cm idatzi dute, 18 cm2 beharko zuen lekuan.
3. Zenbat triangelu egin daitezke hiru erpinak kolore bereko puntuetan hartuta?

Kolore bakoitzeko puntuekin zenbat hirukote egin daitezkeen kalkulatu behar dugu eta hirukotearen puntuak lerro zuzen berean suertatzen diren kasuak kendu.
Sei puntu gorriek (6 x 5 x 4) : (3 x 2) = 20 hirukote ematen dituzte, eta hamar puntu urdinek, (10 x 9 x 8) : (3 x 2) = 120 hirukote. (Konbinazioetarako formula erabili dugu.) Denetara, 140 hirukote ditugu.
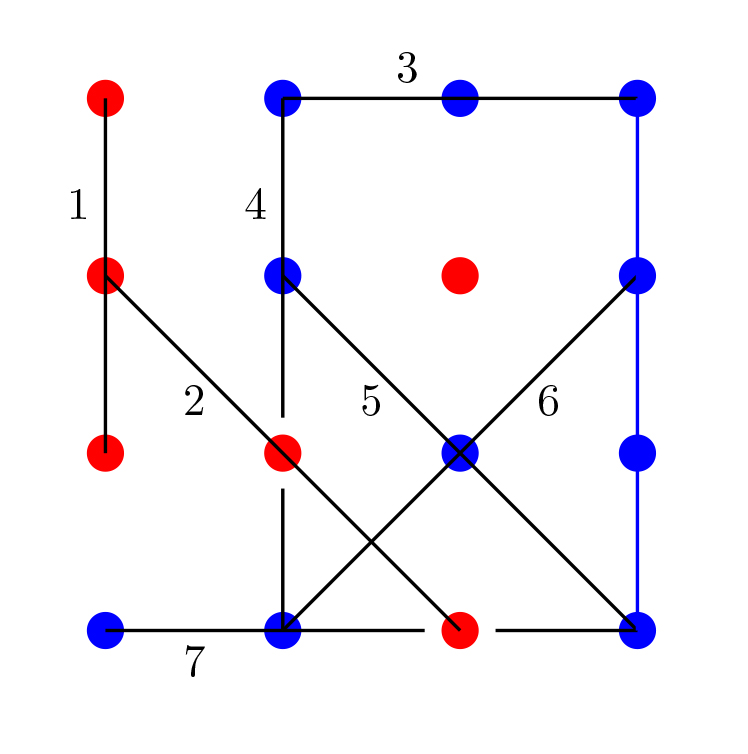
Irudian ikus daitekeenez, bi hirukote gorrik dituzte puntuak lerrokatuta. Urdinen kasuan, alde batetik bost hirukote kendu behar dira (irudiko 3tik 7ra), eta beste alde batetik azken zutabeko lau puntuek kendu beharreko lau hirukote ematen dituzte. Denetara, 11 hirukote kendu behar dira.
Hortaz, 140 – 11 = 129 triangelu egin ditzakegu erpinak kolore bereko puntuetan hartuta.
Joseluk zuzen eman du erantzuna.
Hasierako abc zenbakiak 100 a + 10 b + c adierazten du; amaierako cba, 100 c + 10 b + a izango da. Kenketa eginez, 99 c – 99 a = 99 (c – a) km egin ditu Jonek. Ibili den ordu kopurua t bada, 99 (c – a) = 55 t edo 9 (c – a) = 5 t dugu. Hortik, c – a = 5 ateratzen dugu. Izan ere, c – a 5en multiploa izan behar da eta 0tik 9rainoko zifrak izanik, c – a = 0 edo 5 bakarrik gerta daitezke. Ezarritako baldintzak kontuan hartuta, c = 6, a = 1 eta b = 0 lortzen dira. Hasieran kontagailuak 106 markatzen zuen.
Koldok, Joseluk eta Iñakik zuzen erantzun dute.
Egin dezagun OAB triangelua irudiak erakusten duen moduan.
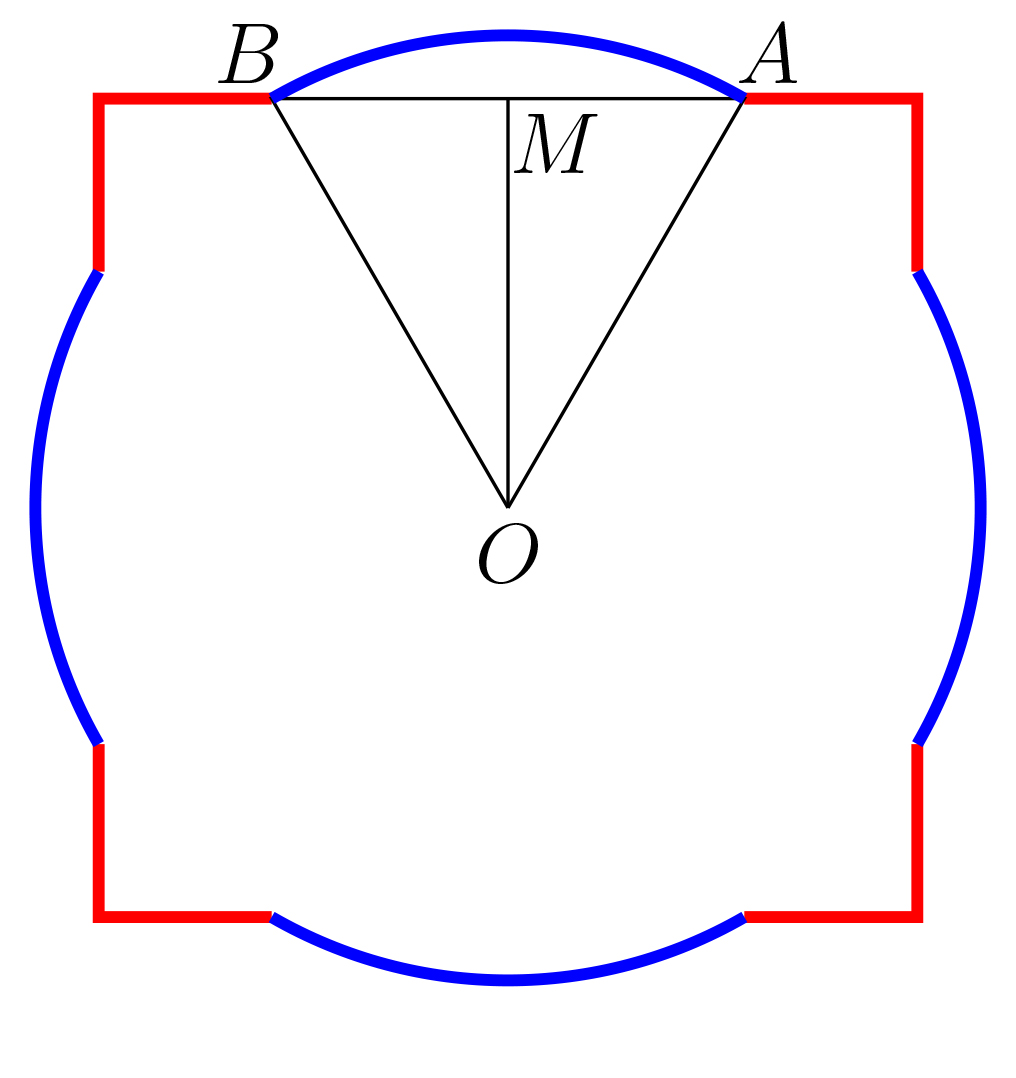
OA = 2 cm (zirkuluaren erradioa) eta OM = √3 cm (karratuaren aldearen erdia) dira. Pitagorasen teorema erabiliz, AM = 1 cm dugu. Beraz, AB = 2 cm da eta OAB triangelua aldeberdina da. Orduan, triangeluaren angeluak 60 o dituzte eta AB arkua zirkunferentzia osoaren seirena da. Zirkunferentziaren luzera 4π denez, 4π/6 = 2π/3 cm da arkuarena. Karratuaren alde bakoitzari 2 cm kendu dizkiogu (AB-ren luzera). Dena kontuan hartuta, irudiaren perimetroa hau da:
4 (2π/3 + 2√3 – 2) = 8 (π/3 +√3 – 1) = 14.23398687…
Mendibero eta Iñakiren erantzunak zuzenak dira.
Bilatzen ari garen zenbakiari 1 gehituta hondar guztiak 0 bilakatuko dira, hau da, 2, 3, 4, 5, 6, 7, 8 eta 9 zenbakien multiploa izango dugu. Hortaz, zenbaki horien guztien multiplo komun txikiena aurkituko dugu. Nahikoa da 5, 7, 8 eta 9ren multiploa izatea, horrek ziurtatzen baitigu 2, 3, 4 eta 6ren multiploa izatea. 5, 7, 8 eta 9ren multiplorik txikiena 5 x 7 x 8 x 9 = 2520 da. Beraz, ariketak eskatzen duen zenbakia 2519 da.
Mendibero eta Iñakiren erantzunak zuzenak dira.
Egileaz: Javier Duoandikoetxea Analisi Matematikoko Katedradun erretiratua da UPV/EHUn.