Duela bost hilabete eskas argitaratu zen Science aldizkari ezaguneko 2016ko urtarrilaren 29ko alea. Aldizkariko azalean ikus daiteke duela 2000-2400 urte inguru idatzitako buztinezko taulatxo babiloniarra. Bertan, idazkera kuneiformea erabiliz Jupiter planetak zeruan duen kokapena nola ezagut daitekeen deskribatzen da.

Mathieu Ossendrijver izeneko Berlingo Humboldt Unibertsitateko paleoastronomo alemana izan da artikuluaren egilea. Azken 13 urteetan zehar, urtero aste bete eman izan du British Museumeko apaletan gordeta dauden milaka taulatxoen artean arakatzen, harik eta taulatxo hori aurkitu eta bertako informazioaren esanguraz ohartu arte. Miresgarria iruditzen zaigu hain jakintza-esparru desberdinak diren astronomia eta paleografia bezalako jakintza-esparruetan aditua izatea.
Burura dakigukeen lehen galdera da ea informazio hori Science aldizkariko azaleko protagonismoa bereganatzeko bezain besteko garrantzitsua ote den. Baiezkoan gaude, abiadura versus denbora grafikoetan irudikatutako trapezoideen areak kalkulatuz kokatzen baitzuten Jupiter antzinako Babiloniako basamortuko zeruan. Horretan datza, hain zuzen ere, taulatxoaren ezaugarririk garrantzitsuenetarikoa, kurba baten azpian geratzen den area kalkulatzea baita funtsezko prozedura Kalkulua deritzon matematiketako esparruan. Historialariek orain arte uste zuten prozedura matematiko hori 1400 urte beranduago asmatu zela Europan XIV. mendean. Hortaz, taulatxo horretako edukia ez da soilik garrantzitsua duela bi mila urte baino gehiago Babiloniako astronomia zein aurreratua zegoen erakusten duelako. Era orokorragoan ere zientziaren historia argitzen laguntzen du.
Babiloniarrek abiadura versus denbora grafikoak erabiliz, astronomia matematikoaren eta matematika geometrikoaren arteko lotura egin zuten lehen aldiz, abiadura versus denbora grafikoak erabiliz.
Abiaduraren definizio moduan ondoko hau hartuko dugu: Higikari batek denbora jakin batean egiten duen distantzia da abiadura. Definizio horren barruan magnitude bi hartzen dira kontuan: denbora eta distantzia. Denbora neurtzeko erabilitako unitatea “eguna” izan zen, eta, trapezoideak irudikatzeko, taulatxoan deskribatutako kalkulu-prozeduran 60 eguneko bi denbora tarte erabili ziren. Kontatzeko sistema sexagesimala erabiltzen zuen kultura batean, “logikotzat” har dezakegu 60 eguneko denbora tarte hori erabiltzea. Bestalde, zein izan zen bigarren magnitudea, alegia distantzia neurtzeko erabili zuten “unitatea”?
Hasiera batean, pentsa genezake egun guk erabiltzen dugun kilometroaren parekoak izan litezkeela babiloniarren luzera-unitateak. Baina nola izan daiteke distantzia neurtzeko babiloniarrek eta guk antzerako unitateak erabiltzea?
Nola? Babiloniarrek dagoenekoz metroa erabiltzen zuten? Jakina ezetz… Orduan?…
Beranduenez ere Kristo aurretiko laugarren milurtekoaren erdialderako, sumertarrek behaketa astronomiko nahikoa zehatzak egiten aritzen ziren. Horren froga modura, 2. irudiko planisferio zaharra ikus daiteke. Bertan, zenbait astroren zeru-sabaiko kokapenak aurki ditzakegu, bi dimentsioko plano batean proiektatuta.

Lurraren eguneko errotazioaren ondorioz, badirudi kurba bat deskribatuz higitzen direla zeru-sabaiko astroak: eguzki, ilargi, izar zein planetak. Antzinateko egiptoarrek uste zuten egunsentian lur azpitik irteten zela eguzkia, azpimundutik argitara itzulita eta antzera gertatzen zela iluntzean Ilargia eta izarrekin. Esan beharrik ez dago, guk geuk ere irudipen hori daukagu.
Zalantzarik ez izan: antzinateko gizakiak, astronomoak ez zirenak ere, laster ohartuko ziren ordu eta irteera- eta sarrera-puntu geografiko desberdinetatik agertzen eta desagertzen zirela astroak.
Demagun duela 5400 urte inguru astronomo sumertar batek, zutik zegoelarik, izar bat bezalako astro baten zeru-sabaian zeharreko ibilbidea jarraitu nahi zuela etengabe parez pare begiratuz. Esan beharrik ez dago, astroarekiko aurrez aurreko begiradari eusteko eta zutik zegoen lekutik oinak mugitu gabe astroaren sarrera-puntura begiratzetik irteera-puntura begira ipintzeko, derrigor biratu beharko zuen gorputza.
Eguzkiaren kasuan, urtaroaren arabera aldatzen dira agerraldiaren iraupena eta zeru-sabaian hartzen duen altuera; Ilargiaren kasuan askoz ere nabariagoak dira ilargialdiko unearen araberako begi bistako iraupena eta tamaina. Eguzkiari adituz, astronomo sumertar hark zehatz mehatz markatu izan balu eguzkia nondik irteten zen eta nondik sartzen zen udaberriko eta udazkeneko ekinozioetan, hau da, egunak eta gauak 12na orduko iraupena dutenean, honako hau ikusiko zuen, alegia, zutik zegoen lekutik, oinak mugitu gabe, eguzkiaren irteera-puntura begiratzetik sarrera-puntura begira ipintzeko, biraketa-norabideari eutsiz, doi-doi beste buelta erdi bat biratu beharko zuen, berriz ere eguzkiaren irteera-puntura begira jartzeko. Hortaz, lurrean marraztutako lerroak, ezker eskuin, erdi-erditik bitan zatituko zuen irteera-puntura begiratzetik sarrera-puntura begiratzera aldatzean astronomoak bere begiradarekin deskribaturiko zirkunferentzia.
Gerora, “Ekialde” izena eman genion udaberri zein udazkeneko ekinozioetako irteera-puntu geografiko bakar horri. Bestalde, “Mendebalde” izendatu genuen bi urtaroetarako sarrera-puntu bakarra.
Gogora bedi hori berdin gertatzen dela Lurraren Ipar zein Hego hemisferioan, eguzkia beti irteten delako ekialdetik eta beti sartzen delako mendebaldetik.
Ekialdera begira ipiniz Eguzkiak zenit izeneko puntu batean hartzen du bere garaiera handiena, eta puntu horri erreparatuz, astronomo sumertar hura konturatuko zen urte osoan zehar zenita beti bere eskuinean geratzen zela, eta horretaz gain, nahiz eta zenita zeru-sabaian gorago edo beherago kokatu, bere altuera urteko egunaren arabera aldatzen baita, zenitaren lurrean gaineko proiekzioa, eguna joan eguna etorri, beti puntu geografiko berdinean ematen zela, eta hortaz, ordu berdinean, eguerdiko 12etan hain zuzen ere. Sumeria Ipar Hemisferioan kokatuta zegoenez, puntu hori mende batzuk beranduago “Hegoa” izendatuko zen.
Era berean, berehalaxe ohartuko zen ezen puntu hori eta bere oinak lotuko zituen lerro bat marraztuko balu, “ekialdea” eta “mendebaldea” elkarren artean lotzen zituen lerroarekiko perpendikular geratuko zela bigarren lerro hori. Gaur egungo terminologia erabiliz, astronomo sumertar haren oinetatik igaroko litzatekeen lerro perpendikularrari tokian tokiko meridianoa deitzen diogu. Behaketa berdina Hego Hemisferioan egingo bagenu, punturik altuena “Iparrean” kokatuko litzateke, hau da, astronomo sumertar hark marraztutako lerroaren beste muturrean, eta doi-doi kontrako alde geografikoan.
Udaberriko ekinozioko eguzkiaren irteera-puntura begira zegoelarik, alegia ekialdera begira, egunak udaberriko ekinoziotik udaburura igarotzen ziren neurrian, konturatuko zen eguzkiaren irteera-puntua bere “ezkerrerago” kokatzen zela egunetik egunera; alegia ikusiko zuen bere eskuinaldeko zirkunferentzierdia pixka bat Iparrerantz luzatzen, eta hortaz, ezkerreko zirkunferentzierdiari zati bat jaten ziola, harik eta udaburura iritsi arte. Bestalde, gauza bera gertatuko zen sarrera-puntuarekin (3. Irudia).
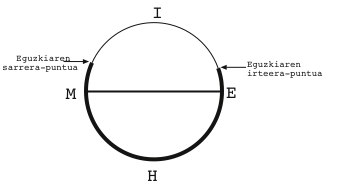
Udazkeneko ekinoziotik neguburura arte egunek laburtzen jarraitzen zutelarik, ekialdera begira zegoen astronomo sumertar hari eguzkiaren irteera- eta sarrera-puntuak bere eskuineko zirkunferentzierdian kokatuko zitzaizkion, oraingo honetan bere eskuinaldeko zirkunferentzierdia pixka bat hegoalderantz txikitzen ari baitzen. Egunetik egunera puntu bi horiek geroz eta eskuinerago, edo, nahi bada, geografiari adituz, geroz eta hegoalderago kokatzen zitzaizkiola behatuko zuen, harik eta behin neguburua igaroz gero, eguzkiaren irteera- eta sarrera-puntuak berriz ere ezkerrerantz, alegia iparralderantz higitzen hasiko ziren arte (4 Irudia).
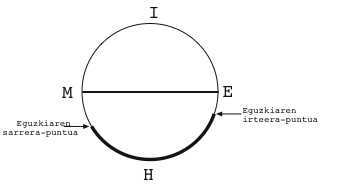
Esan gabe doa, eguzkiaren zeruan zeharreko ibilbidearen mugarri horiek guztiak zehatz-mehatz erregistratzeaz gain, xehe-xehe idatziko zuen noiz jazotzen zen gertaera astronomiko bakoitza, eguneko zein ordutan alegia. Ordurako ezaguna izango zuten eguzki-erlojua, eta erlojuaren gnomona doi-doi zenitera begira jarrita kokatuta edukiko zuten. Baina arazoa honako galdera hau erantzun nahi izan zutenean agertuko zitzaien: Zenbat aldatzen da zenitaren altuera urte osoan zehar, neguburutik udaburura? Zenbat higitzen dira urtean zehar ezker-eskuin eguzkiaren irteera- eta sarrera-puntuak? Goraxeago aditzera eman dugunez, zirkularra da eguzkiaren eta gainerako astro zerutiarren itxurazko higidura.
Beraz, astronomo sumertarren problema zen une oro jakitea kurba baten zeharreko desplazamendua zenbatekoa izan zen. Honako hau izan zitekeen neurtzen hasteko modurik errazena eta, hortaz, garai hartan, duela 5500 baino gehiago, artean ezagunak ziren teknologia eta tresneriaz erabat egingarria izango zena: leku lau batean, plano horizontal batean, zirkunferentzia bat marraztea, planisferio bat eraikitzea hain justu. Horretarako aski zen soka bat eta makila bi edukitzea. Sokaren muturrek begizta bana edukiko zuen, soka makilen inguruan kiribildu ez zedin. Makiletariko batek puntu batean finkatutako ardatz moduan jokatuko zuen eta bigarren makilaren bidez, lehenengoaren inguruan zirkulu baten ingurumaria, alegia zirkunferentzia bat marraztuko zuten. Sokaren luzera zirkunferentziaren erradioa izango zen. Ziur gaude hondartzan denok egin dugula noiz edo noiz halako irudiren bat makilatxo birekin eta oinetakoetako lokarriren batekin.
Lan handirik eskatuko ez zien zirkunferentzia marraztu eta gero, pusketa berdinetan zatikatzea izango zen hurrengo erronka. Ziur gaude marrazketa teknikoaren irakasgaian denok erabili dugula konpasa, lehenik eta behin zirkunferentzia marrazteko eta, bigarrenez, konpasaren zabalera ukitu gabe, hau da erradioa berdin-berdin mantenduz, zirkunferentzia zatikatzeko. Edozein puntutan finkatu konpasaren orratza, erradioari dagokion distantziara zirkunferentzian marratxo bat egin, hurrengo urratsean bertan kokatu konpasaren orratza eta berriz zirkunferentzian beste marratxo bat egin; horrela sei aldiz egiten genuen, ingurumaria osoan zehar bira osoa eman arte eta hasierako puntura iritsi arte. Puntuok zuzenekin lotuz, hexagono bat lortzen genuen. Bai, ezta?

Demagun ekinozioaren egunean eguzkiaren irteera-puntua kokatuta zegoen tokian, hau da Ekialdean, finkatzen zutela zirkunferentzia zatikatzen hasteko lehen puntua. Hirugarren mozketa-puntua bat etorriko zen eguzkiaren egun horretako sarrera-puntuarekin, hau da Mendebalarekin.
Puntu biek, elkarrekin zuzen baten bidez lotuz, Ekialde-Mendebalde ardatza finkatuko zuten. Zatitzeko prozedura honen erraztasuna oso agerikoa zen, baina bazuen bigarren hobari nabarmen bat astronomo sumertar haiek balia zezaketena. Hexagonoa marraztu ondoren, berehalaxe konturatuko ziren ezen alde bi (ab & cd, 6. Irudia) Ekialde–Mendebalde ardatzarekiko paraleloak zirela.
Ziur aski denok aurkitu ditugu gure kabuz alde bi horien erdiko puntuak konpas bat eta erregela bat erabiliz, eta sumertarrek ere hala egingo zuten, ondoren erdiko puntuak elkarrekin lotu eta Hegoa edota zenitaren puntua seinalatzen zuen lerroa lortzeko. Lerro hori Ekialde-Mendebalde ardatzarekiko perpendikularra izango zen. Era erraz horretan zehazki finkatuta geratuko zitzaizkien lau puntu kardinalak. (6. Irudia)
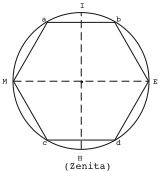
Sistema sexagesimala erabiltzen zuen zibilizazio horrek eta beraz, orduak 60 pusketatan zatikatzen ziren era berean, 60 pusketatan zatikatu zen hexagonoaren aldeek zedarritutako zirkunferentziaren sei sektoreetako bakoitza. Hasieran zaila dirudi sektore horietariko bakoitza 60 zati berdinetan banatzeak, baina hexagonoak lana erraztuko zien trikimailua eskaintzen zien. Bigarren hexagono bat marraztuko zuten baina oraingo honetan konpasaren orratza hexagonoaren bidez finkaturiko 6 arkuetako baten erdiko puntuan ipiniko zuten zirkunferentzian lehen zatiketa-marka (6. irudia) zenita kokatua zegoen tokian esate baterako. 8. Irudiko 4 puntua Ekia bazen eta 10 puntua Mendebala, 7an kokatuko zen Hegoa (zenita) eta bertatik has zitezkeen bigarren hexagonoa marrazten.
Era honetan, zailtasun handirik gabe eta tresneria xinple batez (makila bi, soka bat eta erregela bat), hexagono bien artean 6 diametro marraz zitekeen, hexagono bakoitzaren erpin bakoitza zirkunferentziaren kontrako aldean zegoen hexagono berberaren erpinarekin lotuz. Ondorioz, zirkunferentzia 12 atal berdin-berdinetan zatituta geratuko zen.
Hamabiko zati kopuru horrek garrantzia handia zuen, izan ere bat egiten baitzuen sumertarrek erabiltzen zuten kontaketa-sistema hamabitarraren oinarriarekin (12arekin alegia).
Prozedura berbera baliagarria zen bai buztinezko edo egurrezko xafla txiki batean marraztutako planisferio eramangarri bat egiteko, bai eta zein etxeko teilatu lau batean edo mendi puntan eraikitako behatoki astronomiko bateko planisferio handi bat egiteko. Dena egongo zen sokaren luzeraren menpe, berak mugatuko baitzuen zirkunferentziaren erradioa. Era berean, beharrezkoa izango zen “erregela” zuzen bat, erradioaren luzeraren bikoitza baino luzeagotxoa izan beharko zena, zirkunferentziaren diametroa erraz marraztu ahal izateko.
Sei zatietako bakoitza 60 zatitan banatuta, zirkunferentzia 360 pusketatan banatzea lortuko genuke. Pusketa bakoitza “gradu” bati dagokio, eta “º” ikurrarekin adierazten da. 360º-ko kopuru hori urteko egunen kopuruarekin ia-ia bat datorrenez, egun bakoitza ia-ia “gradu” bati legokioke; izan ere urte astronomiko batean eguzkiak zirkunferentzia osoa egiten du, eguzkiaren zeruan zeharreko ibilbideak lurreko gure ikuspegitik analema itxura hartzen duen arren. 360º-ko kopuru horrek eskaintzen dituen abantaila matematikoak begi-bistakoak egiten zaizkigu, zirkunferentzia tamaina ezberdinetako pusketatan banatu nahi dugunean. Esate baterako, 7a da lehen hamar zenbakietatik 360ren zatitzaile bakarra emaitza moduan zenbaki osoa ematen ez duena; alegia 360 zati 2, zati 3, zati 4, .., zati 10, denek ematen dute zenbaki osoa, 7ak salbu. Interesa daukanak egin dezala aproba 400ekin eta ikusiko du aldea.
Hexagonoaren diagonalak marraztean konturatuko gara sei triangelu aldeberdin eratu zaizkigula. Zirkunferentziaren zentroan bat egiten duten sei triangeluen angeluek, definizioz (360/6), bakoitzak 60º-ko balioa izango du (7. Irudia). Triangelu aldeberdineko hiru barne angeluak berdinak direnez, triangelu baten barne angeluen batura 180º-koa izango da, zirkunferentzia erdiaren parekoa. Zirkunferentzia bi diametro elkartzuten bidez laurdenduko bagenu, lau angelu zuzen lortuko genituzkeenez, angelu zuzen bakoitzak 90º-ko balioa hartuko luke.
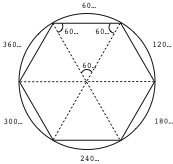
Bi hexagono horietariko bakoitzaren alde bakoitzak bi puntutan mozten du beste hexagonoaren alde bakoitza.

Ebakipuntu bakoitzetik igarotzen den diametroa marraztuko bagenu, 8. Irudiko 12 zatietariko bakoitza doi-doi erdibituko genuke, eta ondorioz, zirkunferentzia 24 atal berdin-berdinetan zatituta geratuko litzaiguke (9. Irudia). Bat-batean, ohartuko gara 24 zatiak bat datozela egunaren ordu kopuruarekin, eta beraz, eguzki-erloju bat egiteko oinarria marraztuta daukagula eta soilik falta zaigula itzala proiektatzeko egokiro kokatutako gnomon bat. Ez izan zalantzarik, prozedura sinple honek erlojugileei zirkunferentzia 12 edo 24 atal berdinetan zatitzeko eskaintzen dien erraztasuna izan dela oraindik orain eguna 24 ordutan banatzearen arrazoietariko bat.

Egileez: Estitxu Txurruka biologoa da eta UPV/EHUko ikertzaileak prestatzeko programaren bekaduna da. Jesus Mari Txurruka UPV/EHUko Genetika, Antropologia Fisikoa eta Animalien Fisiologia Saileko irakaslea da.