Hizkuntza matematikoa egunero elkarrekin komunikatzeko erabiltzen dugun hizkuntzaren parte diren letrek eta zenbakiek osatzen dute, baina, era berean, zientzia horrek berezko dituen ikur matematiko ugari ere badira. Ahalik eta sinpleen izan behar duten ikur horien helburua zera da: hizkuntza matematikoa hizkuntza jakin bati lotuta ez dagoen eta planetako edozein pertsonak uler dezakeen hizkuntza unibertsala bihurtzea, pertsona horiek hizkuntza edo bizilekua edozein izanda ere.

Ikur matematikoek, gure kulturako beste edozein osagaik bezala, historia propioa dute, gurea ere badena, hots, gizadiarena. Gaurko artikulu honetan, gure eguneroko hizkuntzaren parte diren oinarrizko ikur matematiko batzuen jatorria aztertuko dugu: lau eragiketa aritmetiko nagusiak (batuketa, kenketa, biderketa eta zatiketa) eta “berdin” zeinua.
Harrisek ipuinari buruzko teoria bitxi bat zuen. Haren ustez, ipuina eragiketa aritmetiko bat baino ez zen. Ez zifren arteko eragiketa bat, jakina, maitasunaren, gorrotoaren, itxaropenaren, desiraren, ohorearen eta antzeko osagaien arteko batuketetan eta kenketetan oinarritutakoa baizik. Abraham eta Isaaken istorioa, adibidez, errukiaren eta aita-semeen arteko maitasunaren batuketa litzateke. Evarena, aldiz, kenketa argia izango litzateke: Jainkoarekiko maitasuna ken munduarekiko maitasuna. Horrez gain, Harrisen arabera, batuketek amaiera zoriontsua duten ipuinei bide eman ohi diete. Kenketetan oinarritutakoek, ordea, amaiera tragikoa izan ohi dute (Obabakoak, Bernardo Atxaga, 1988).
+ (batuketa) eta – (kenketa) ikurrak
+ (plus) eta – (minus) ikurrak liburu inprimatu batean erabili ziren lehendabiziko aldiz, Leipzigen 1489an argitaratutako Johannes Widman (1462-1498) matematikari alemaniarraren Mercantile Arithmetic, edo Behende und hubsche Rechenung au allen Kau manscha obran, hain zuzen. Hala ere, Widmanek ez zituen + eta – ikurrak batuketa eta kenketa eragiketa aritmetikoen sinbolo gisa erabiltzen, baizik eta testuan aztertzen diren merkataritzako praktiken testuinguruan, salgaien gehiegikeria edo gabezia adierazteko, adibidez, upelen pisuari zegokionez. Irudi honetan “4 + 5” (“4 centner + 5 pfund” esanahiarekin) edo “5 – 17” (“5 centner – 17 pfund” adierarekin) irakur daiteke, non “centner” eta “pfund” pisu-unitate alemaniarrak diren, eta “centner” bat 100 “pfund” diren eta, aldi berean, 50 kilogramori dagokien.

Van der Hoeke (XVI. mendea) matematikari herbeheretarraren aritmetikako liburua + eta – ikurrak eragiketa aljebraiko gisa ageri diren lehen argitalpen inprimatua dela esan ohi da, 1514ko obratzat jo izan delako, baina egiatan 1937an argitaratu zen (1514ko data 1944ko edizioarekin lotutako akats bat da). Florian Cajorik aipatzen duen bezala, ikur horien adiera aljebraikoa aintzat hartu zuen lehen argitalpen inprimatua Henricus Grammateus (1492-1525 inguruan) matematikari alemaniarraren Ayn new Kunstlich Beuch (1518) aljebra eta aritmetikako liburua da.
Hala ere, hura ez da + eta – ikurren lehen agerraldia, dagoeneko latinez eta alemanez idatzitako XV. mendeko azken hogei urteetako Alemaniako zenbait eskuizkributan topa daitezkeelako. Dresdeko Liburutegian bada eskuizkribu bilduma bat (MS C80), eta bertan, agian lehendabiziko aldiz, + eta – ikurrak ageri dira. Widmanek eta Grammateusek eskuizkribu horiek ezagutzen zituzten.
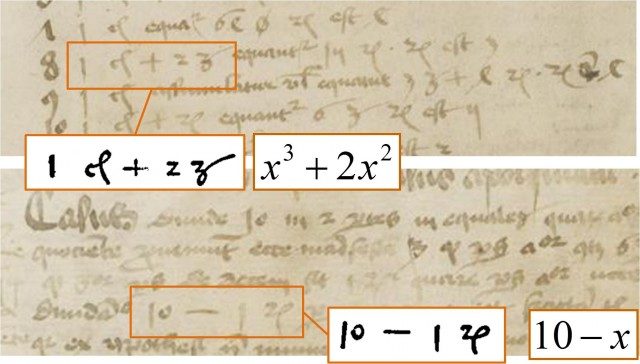
+ ikurraren gurutze forma latindarra eskuizkribuetan “et” juntagailua, hots, “eta” konjuntzioa batuketa adierazteko erabiltzearen emaitza da; alde horretatik, gaur egun oraindik ere “bi eta bi lau dira” esaten dugu. + ikurra “et” juntagailuaren laburdura bat da, izan ere, ikertzaile batzuek testu latindarretan “et” terminoaren ehun laburduratik gora zerrendatu dituzte, eta haietako bat + gurutzea litzateke (“t” letraren idazkera irudikatu dezagun). 1417ko lehen eskuizkribu horietako batean + gurutze bat ageri da, baina marra bertikala atzerantz etzanda duela.
Baliteke Nikolas Oresmekoa (1323-1382) matematikariak 1356 eta 1361 urteen artean idatzitako Algorismus proportionum obra izatea + ikurra eskuizkribu batean agertu zen lehen aldia. Hala ere, litekeena da + ikurra jatorrizko obran egon ez eta beranduago kopiagile batek idatzi izana.
– ikurraren jatorria zalantzazkoagoa da; izan ere, badira hura azaltzen saiatzen diren teoria ezberdinak. Haietako batek planteatzen du jatorria hau izan daitekeela: merkatariek salgaien pisu osotik tara (denbora luzez “minus” esan zitzaiona), hots, produktuaren ontziaren pisua bereizteko erabiltzen zuten barra horizontala. “Minus” hitzaren laburdura ere izan daiteke. Beste teoria baten arabera, Diofano Alexandriakoa (III. mendea) matematikari greziarrak “minus” adierazteko erabili zuen ikurretik erator daiteke; jatorrian goiko partea moztuta duen alderantzizko psi bat zen, zeinuaren antzekoa, baina marra bertikal batek alboko bi lerroak zeharkatzen zituen, eta forma horretatik “t” larri moduko bat eratorriko zen, oina galtzean – ikurrari bide emango ziona. Egiptoko sinbolo hieratiko batean ere izan dezake jatorria.
XV. mendea baino lehen, Italian, beste leku askotan bezala, idatzizko hizkuntzan “plus” eta “minus” hitzak erabili ziren, eta laburduraren bidez “p” edo “m” letrak (baita gainean tilde bat edo segmentu bat zutenak ere) eratorri ziren batuketa eta kenketa adierazteko. laburdurak Luca Pacioli (1447-1517) matematikari italiarraren Summa de arithmetica, geometria, proportioni et proportionalita (1494) obran agertu ziren lehendabiziko aldiz, eta XV. eta XVI. mendeetan zehar erabili ziren. + eta – ikur alemaniarrak Italian erabiltzen hasi ziren XVII. mendean.

Britainia Handian, + eta – ikurrak, “berdin” adierazten duen = zeinuarekin batera, The Whetstone of Witte liburuan erabili ziren lehendabiziko aldiz, 1557an. Espainian eta Frantzian + eta – ikur alemaniarrak, zein “p” eta “m” sinbolo italiarrak erabiltzen ziren.
Batuketa adierazten zuen + gurutzeak ere hainbat forma hartu zituen. Forma nagusia, gaur egun oraindik ere erabiltzen duguna, gurutze grekoa izan da beti. Baina gurutze latindarra ere erabili zen, maiz horizontalean ageriz (parterik luzeena eskuinean edo ezkerrean zuela). Eskandinavian San Jorgerena deritzon gurutzea, edo haren aldaera den Maltako gurutzea neurri txikiago batean erabili ziren.

– kenketarako ikur sinplea izan arren, matematikari talde batek ÷ sinbolo konplexuarekin hura ordezkatzea erabaki zuen, eta harrezkero laurehun urtez erabilia izan zen, baita puntua goiko partean baino ez zuen aldaeraren modukoak ere txertatuta. Kenketaren ikur gisa, bi marra jarraitu “– –” edo hiru marra jarraitu “– – –” ere erabili ziren.
Jakina, horien aurretik batuketa eta kenketa adierazteko beste ikur batzuk baliatu ziren. Adibidez, babiloniarrek idazkera kuneiformean batuketarako ideograma bat erabiltzen zuten (“tab”, punta beherantz zuzenduta zuen triangelu isoszelea), eta beste bat kenketarako (“lal”, punta eskuinerantz zuzenduta zuen triangelu isoszelea). Ahmesen papiro egiptoarrean aurrerantz ibiltzen ari diren bi hanka erabiltzen dira batuketarako, eta atzerantz dabiltzan beste bi hanka kenketarako.

× eta · ikurrak (biderketa)
Florian Cajorik bere liburuan aipatzen duen moduan, hauek dira biderketa adierazteko ikur horien zenbait aurrekari. Babiloniarrek berriz ere ideograma bat erabili zuten, “a-du” izenekoa, biderketa irudikatzeko. Diofantok ez zuen inolako ikurrik erabiltzen. Indiako matematikari buruzko eskuizkriburik zaharrena den Bakhshiili manuscript lanean faktorea beste aldean kokatuta ageri da. Bhaskara Acharia (1114-1185) matematikari indiarrak “bhavita” (edo “bha” laburdura) idazten zuen faktoreen ondoren.
Zenbait matematikarik —Michael Stifel (1487-1567) matematikari alemaniarrak Deutsche Arithmetica (1545) obran, Simon Stevin (1548-1620) matematikari flandestarrak, edo René Descartes (1596-1650) filosofo eta matematikariak Géométrie (1637) lanean— M letra erabili zuten biderketa adierazteko, eta D letra zatiketarako. Esate baterako, Stevinek edo Stiefelek “3①Msec①Mter②” espresioa idatzi zuten, non “sec” bigarren aldaera edo kopuru ezezaguna eta “ter” hirugarrena diren, aurrean zenbaki bat duen zirkuluak aldaera horren berretura adierazten duen, eta M eta D letrak biderketa eta zatiketaren zeinuak diren. Guk hala adieraziko genuke: 3 x y z2. Era berean, haiek “5②Dsec①Mter②” idatzi zuten guk “5 x2 z2 / y” gisa irudikatuko genukeena adierazteko.
Bestalde, Francois Vieta (1540-1603) matematikari frantsesak “a b-ren barruan” espresioa erabiltzen zuen a eta b aldaeren emaitza adierazteko.
William Oughtred (1574-1660) matematikari ingelesaren Clavis Mathematicae (1631) obran erabili zen lehendabiziko aldiz San Andres gurutzea × biderketaren sinbolo gisa. Edward Wrightek 1618an John Napier (1550-1617) matematikari eskoziarraren Descriptio (1614) obraren itzulpenaren eranskin anonimo batean “x” letraren formarekin ageri bada ere, badirudi eranskina Oughtredek berak idatzi zuela.
Oughtredek gurutze txiki bat —San Andres gurutzea— erabiltzen zuen; Adrien-Marie Legendre (1752-1833) matematikari frantsesak, aldiz, Elements de Gèomètrie (1794) lanean gurutze handi bat baliatu zuen. Biderketaren × ikurra gure egunetara iritsi da, nahiz eta haren erabilera ez den guztiz orokortu, funtsean matematikaren arloan erabiltzen den puntuaren ikurra ere badugulako.
Britainia Handian × ikurra oso zabalduta bazegoen ere, matematikari batzuek, hala nola Isaac Newton (1643-1727) matematikari ingelesarekin batera kalkuluaren asmatzailea izan zen Gottfried W. Leibniz (1646-1716) matematikari alemaniarrak, ez zuten sinbolo hori atsegin. Johann Bernoulli (1667-1748) matematikariari Basiletik (Suitza) bidalitako gutun batean hauxe esan zion: Ez dut × sinboloa gustuko biderketarako, “x” batekin nahastu daitekeelako (…) bi kopuru puntu baten bidez lotu eta biderketa RS·PQ adieraziz seinalatzen dut maiz.
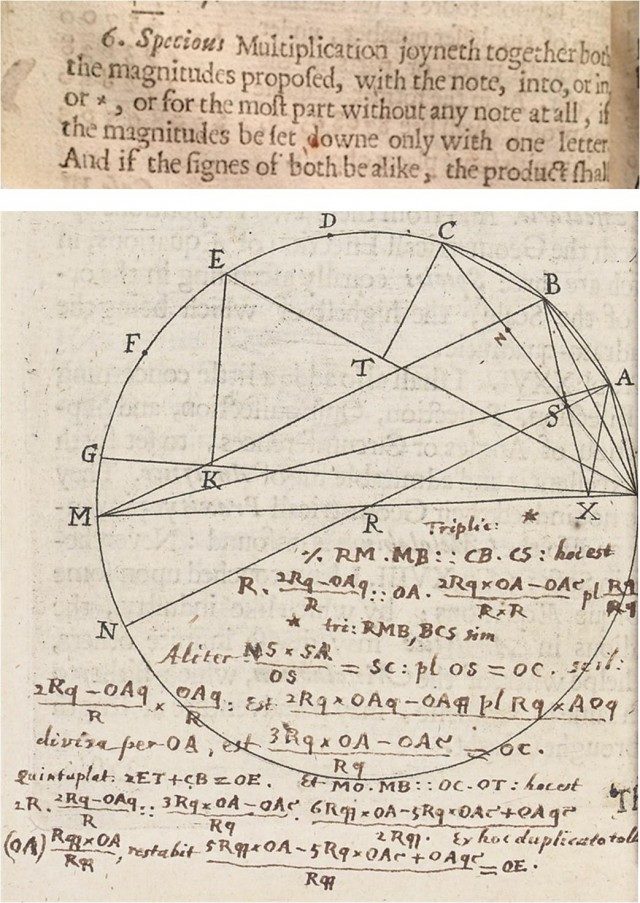
Biderketa adierazteko puntua txertatu zuena Leibniz izan zela esan daitekeen arren, lehenago ere agertu zen. Adibidez, Thomas Harriotek Artis analyticae praxis (1631) lanean puntua darabil “aaa – 3 · bba = +2 · ccc” espresioan. Puntua, azkenik, matematikaren arloan XVIII. mendean onartuko zen biderketaren sinbolo gisa.

Emaitza adierazteko beste sinbolo batzuk izan ziren; esate baterako, Johann Rahn (1622-1676) matematikari suitzarrak Teutsche Algebra (1659) obran * izartxoa baliatu zuen, eta hasiera batean Leibnizek parte irekia beherantz kokatutako C etzan bat erabili zuen Dissertatio de arte combinatoria (1666) lanean.
: eta / ikurrak (zatiketa)
Aurreko ikurrekin ikusi dugun bezala, babiloniarrek, greziarrek edo Indiako matematikariek zatiketa irudikatzeko modu ezberdinak zituzten, baina kasu askotan ikur berbera erabiltzen zuten zatikietarako; hala ere, guk zatiketaren eragiketan erabili izan ziren sinbolo modernoagoak aztertuko ditugu.
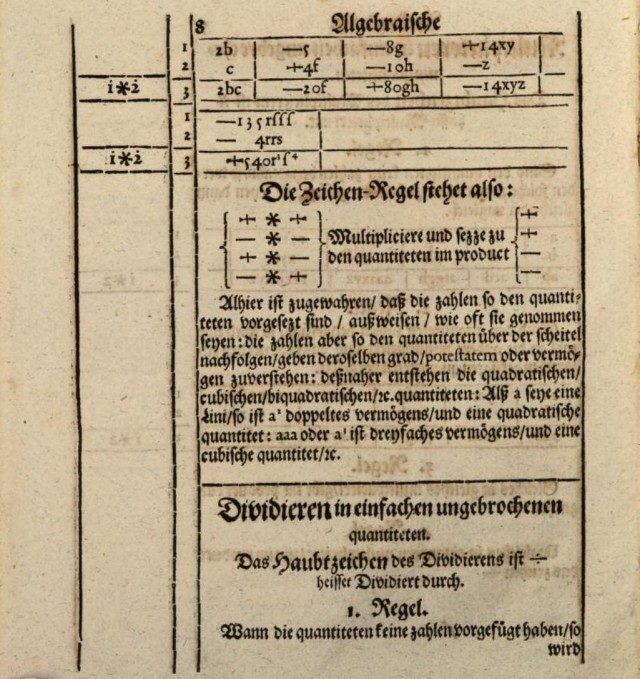
Zatiketarako ikur moderno horietako bat “ilargi-ikurra” edo zenbakien artean kokatutako parentesia da. Hala, 24 zati 8 eragiketa adierazteko, “8)24” idazten zen. Ikur hori Michael Stifel matematikari alemaniarraren Arithmetica integra (1544) obran, edo Joseph Moxon (1627-1691) hidrografoak osatutako termino matematikoei buruzko ingelesezko lehen hiztegian topa dezakegu, non “D)A+B–C” idazten duen guk “(A + B – C) : D” irudikatuko genukeena adierazteko.
Bi “ilargi-ikur” edo parentesi ere erabili zituzten, beraz, “24 zati 8” eragiketa “8)24(” idatzita aurki daitekeen. Idazkera hori denbora luzez erabiltzen jarraitu zuten, zatiketaren emaitza eskuinean ere kokatuz, parentesiaren bestaldean; hala, “24 zati 8 berdin 3” eragiketa “8)24(3” adierazten zen.

Lehen aipatu dugun moduan, Michael Stiefel bera, Deutsche Arithmetica (1545) obran, M eta D letrak erabiltzen hasi zen biderketa adierazteko. D marka beste autore batzuek ere baliatu zuten, haietako zenbaitek alderantzizko D bat ere bai —J. E. Gallimard (1685-1771) frantsesak bezala—; beste batzuek, aldiz, “d” etzan bat idazten zuten —adibidez, J. A. da Cuhna (1744-1787) portugaldarrak—.
Gaur egun arte bizirik iraun duen zatiketaren ikurretako bat goiko eta beheko parteetan puntu bana dituen marra bat da. Sinbolo hori John Rahn matematikariak txertatu zuen lehendabiziko aldiz Teutsche Algebra (1659) obran.

Sinbolo hau mundu anglosaxoian (Britainia Handian eta AEBn) erabili zen, ez ordea europar kontinentean, eta gerora hura erabiltzeko ohitura galduz joan zen, nahiz eta oraindik ere ikur ezaguna den. Izan ere, horixe da kalkulagailuetan zatiketarako erabiltzen den sinboloa.
Gottfried W. Leibniz matematikari alemaniarrak, Dissertatio de arte combinatoria (1666) obran, parte irekia gorantz irudikatutako C etzan bat erabiltzen zuen zatiketa adierazteko. Baina beranduago, kalkulu infinitesimala aipatzen duen lehen lana bihurtuko zen “Nova Methodus pro maximis et minimis, itemque tangentibus, et singulare pro illis calculi genus” artikuluan (Acta eruditorum, 1684), idazkera hura baztertu eta, haren ordez, : bi puntuak erabiltzeari ekin zion. Leibnizek berak azaldu zuen, harrezkero, zatiketa adierazteko “x : y” espresioa erabiliko zuela, “x zati y” esan nahi duena.
Leibnizen arabera, testu batean bi puntuak erabiltzearen abantailetako bat da zatiketa lerro berean mantendu daitekeela eta, marra horizontalarekin idazten denean ez bezala, ez dagoela norabide bertikalean espazioa handitu beharrik, lerroak are gehiago bereiztea eskatuko zukeena, bide batez.

Leibnizek Johann Bernoulliri biderketaren inguruan idatzitako gutunaren aurreko aipamenak hala jarraitzen zuen: Arrazoia aipatzeko, puntu bakar baten ordez, bi erabiltzen ditut; eta ikur hori bera baliatzen dut zatiketarako. Horrela, zuk erabiltzen duzun “dy . x :: dt . a” espresioaren ordez, nik “dy : x = dt : a” idazten dut, hau da: dt a-rekiko den bezalakoa da dy x-ekiko; hots, dy zati x, eta dt zati a, berdina da.
Europar kontinentean, Leibnizek biderketarako (· puntua) eta zatiketarako (: bi puntuak) baliatu zituen idazkerak berehala onartuak izan ziren.
Era berean, Leibnizek, bi puntuak azaltzeko, zatikizuna eta zatitzailea marra horizontal baten gainean eta azpian idazten diren zatiketa-ikurraren erabilera aipatu zuen. Gaur egun ere arlo matematikoan eta hartatik kanpo oso erabilia den idazkera honek antzinatean du jatorria; hala iradokitzen du, behintzat, espresio konplexuak adierazteko erakusten duen moldakortasunak. Gauza jakina da marra horizontala arabiarrek txertatu zutela, nola izan zen edo nork egin zuen ez badakigu ere. Europan Fibonacci, Leonardo de Pisa (1180-1250) matematikaria izan zen marra horizontala lehendabiziko aldiz erabili zuena (izan ere, Fibonaccik Europara ekarri zituen gaur egun darabiltzagun zenbaki indoarabiarrak, arabiarrengandik jaso eta gero).
Bestalde, gaur egun zatiketa adierazteko hainbeste erabiltzen den marra etzana XVIII. mendeko liburu inprimatuetan zatiketari zegokion marra horizontala irudikatzeko baliabide tipografiko bat baino ez zen.
= ikurra (berdin)
= ikurra Robert Recordek baliatu zuen lehendabiziko aldiz The Whetstone of Witte (1557) aljebrako liburuan. Recordek zioen ez zegoela bi lerro paralelo baino gauza berdinagorik, eta, horregatik, = sinboloa erabili zuen bi gauzen arteko berdintasuna adierazteko. Hala ere, denbora luzea igaro zen = ikurraren erabilera zabaldu arte. 1618. urtera arte ez zen liburu inprimatu batean agertu, 61 urte igaro ondoren, hain justu. Ingalaterran 1631. urtetik aurrera hedatuko zen, urte hartan sinbolo hori agertzen zen hiru obra garrantzitsu argitaratu baitziren: Thomas Harrioten (1560-1621) Artis Analyticae Praxis, William Oughtreden Clavis Mathematicae, eta Richard Norwooden (1590-1675) Trigonometrie, or the Doctrine of Triangles.
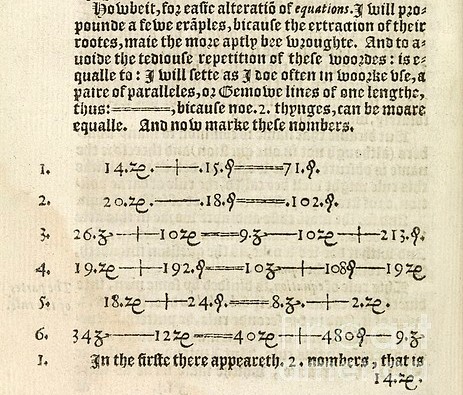
Recordek = ikurra zabaldu aurreko liburu inprimatuetan, baita mende oso bat beranduago ere, “aequales”, “aequantur”, “esgale”, “faciunt” eta beste hainbat hitz erabili ziren bi gauza berdinak zirela adierazteko, “aeq.” laburdura barne. Ez zuten inolako sinbolorik erabiltzen berdintasuna adierazteko. Beraz, ikurraren ordez, aipatutako hitzak topatuko ditugu Kepler, Galileo, Torricelli, Cavalieri, Pascal, Napier, Briggs, Gregory St. Vincent edo Fermat matematikarien obretan.
Komunitate zientifikoak, batez ere matematikarien arlokoak, denbora asko behar izan zuen Recorderen ikurra onartzeko, eta, horrez gain, “=” ikurra jada beste esanahi batzuekin baliatzen zen. Vietak, adibidez, aldea, hots, bi kopururen arteko kenketa adierazteko baliatu zuen; hala, “9 = 6 aequale 3” idazten zuen. 1638an, Descartesek gaur egungo ± zeinuaren adiera berarekin erabili zuen (hau da, “x = ± 1” espresio bat da, non “x” letra “1 edo -1” izan daitekeen). Gauzen berdintasuna adierazteko beste ikur batzuk ezartzen saiatu baziren ere, XVIII. mendean Recordek proposatutako zeinua nagusitu zen argitalpen matematiko eta zientifikoetan.
Bestetik, berdintasun matematikoa irudikatzeari dagokionez, baziren = bi lerro paraleloekin lehian zeuden beste ikur batzuk. Zeinu askoren artean, haietako zenbait eskuineko kortxetea, bi lerro bertikal paraleloak || eta lerro bertikala | izan ziren.

Aurreko irudian Joannes Buteo (1492-1572) matematikari frantsesaren Logistica quae & Arithmetica vulgò dicitur in libros quinque digesta … eiusdem ad locum Vitruuij corruptum restitutio, qui est de proportione lapidum mittendorum ad balistae foramen, libro décimo (1559) liburuko bi orrialde ikus daitezke. Bertan, besteak beste, “1 A,1/3 B,1/3 C[14” eta “3 A.3B.15C[120” espresioak ageri dira, Florian Cajoriren arabera, egungo idazkera matematiko modernoa baliatuta, hala adieraziko liratekeenak: y (batuketa, koma eta punturako idazkera ezberdinak ditugu).

Iturriak
- Alejandro Guijarro, Momentum argazki-erakusketa (2010-2013), divulgamat webgunean ikus daitekeena.
- Florian Cajori, A history of mathematical notations (I. eta II. liburukiak), Dover, 1993 [The Open Court Company argitaletxeak 1928an argitaratutako jatorrizko edizioa doan kontsulta daiteke Internet Archive webgunean]
- Vicente Meavilla, Eso no estaba en mi libro de Matemáticas, Almuzara, 2012.
- Saxon State and University Library Dresden (SLUB)
- Jeff Miller, Earliest Uses of Various Mathematical Symbols
- Stephen Wolfram, Dropping In on Gottfried Leibniz
- Frank J. Swetz, Mathematical Treasure: Leibniz’s Papers on Calculus, Mathematical Association of America.
- René Descartes, Obras de René Descartes (Charles Adam eta Paul Tanneryren edizioa), 1905. Acceso libre en Wikisource
- Joannes Buteo, Logistica quae & Arithmetica vulgò dicitur in libros quinque digesta… eiusdem ad locum Vitruuij corruptum restitutio, qui est de proportione lapidum mittendorum ad balistae foramen, libro décimo (1559), Fondo Antiguo, Sevillako Unibertsitatea.
Egileaz: Raúl Ibáñez UPV/EHUko Matematika Saileko irakaslea da, dibulgatzailea eta Kultura Zientifikoko Katedrako kolaboratzailea.