Eredu dinamikoak matematikaren irakaskuntzan

Aitzol Lasa Oyarbide

Matematikak giza jardueraren parte dira, eta, giza jarduera ororen modura, esanahia hartzen dute ereduak eraikitzerakoan eta problemen ebazpenerako testuinguruetan. Horrez gainera, problema matematiko horiek ebazterako orduan, tartean dauden ezagutza matematikoak dimentsio anitzekoak dira eta pertsonaren jarduera konplexua da.

Honenbestez, ikasgela barruko jarduera matematikoak kontuan hartu behar du giza errealitate hori, eta, horregatik, eskolako testuinguruan diseinatzen diren ikaskuntza eta irakaskuntza egoerek kontuan hartu behar dituzte, besteak beste, ikasle bakoitzaren iragana eta etengabean aldatuz ari den ingurunea. Izan ere, jarduera matematikoa ikasgelaren memoria didaktikoan gordeko da.

Testuinguru horretan, irakasleari dagokio praktika operatiboa eta diskurtsiboa kudeatuko dituzten tresnen aukeraketa. Tresna horien bidez eraiki eta komunikatuko ditu ikasleak bere ezagutzak ingurune didaktikoan, eta bere produkzioak kontrolatu beharko ditu.

Tresnaren aukeraketa pragmatikoa izan daiteke, hau da, tresnak dituen abantaila teknikoak baliatu nahiko dira. Hala ere, ez dira ahaztu behar tresna horrekin komunikatu nahi diren jakintza matematikoari loturiko beste ezaugarri batzuk. Hau da, tresnaren erabilera efektiboa dela ziurtatu behar da, eta, bereziki, irristatze metakognitiborik ez dagoela egiaztatu behar da. Fenomeno horren arabera, erabilitako tresnaren instrukzioak ordezkatu egiten du ikaskuntzaren edukia bera.

Gaur egun, tresnaren aukeraketa aurrerapen teknologikoei loturik dator, ezinbestean. Matematikaren irakaskuntzarako ingurua aldatzen ari da etengabean, aukeraturiko tresnaren eta eduki matematikoaren arteko harremana bera ere aldatzen delarik.

Hori guztia dela eta, irakasleak kontaktuan egon behar du berrikuntza teknologiko eta instrumentalekin, tresna horien balizko erabilera baloratzeko.

Eredu dinamikoa eta gardentasunaren ilusioa

Objektu geometrikoak ohiko arbelean irudikatzerakoan, irakasleak denbora-muga nabarmena izango du. Saio bakoitzean, ilustratu nahi dituen objektu geometrikoen adibide bat edo adibide gutxi batzuk besterik ezingo ditu irudikatu. Adibide horiek gardentasunaren ilusioa eragin dezakete, hau da, irakasleak adibidea eredu gisa interpretatzen duen arren (klase bateko ordezkari gisa), ikasleak adibide hutsa besterik ez du ikusten.

Fenomeno horrek agerian uzten du distantzia bat, hots, matematika jarduera zientifikoaren eta eskolako eduki matematiko kristalizatuen arteko distantzia. Matematikaren komunikazio eta eraikuntza dinamika guztietan agertuko da fenomeno hori.

Ezinbestekoa da ikasleak eta irakasleak “hizkuntza bera” hitz egitea, eta, horretarako, ikasgelan erabilitako tresnak aukera eman behar du landutako eduki matematikoei esanahi partekatu bera emateko. Horrela, eredu dinamikoen erabilera fenomeno horri aurre egiteko lagungarria da. Hau da, objektu matematiko batek bi esanahi ditu, “objektu bakandua” da eta baita “klase bateko ordezkari” ere, eta eredu dinamikoak laburtu egiten du bi interpretazio horien arteko distantzia. Orokortze prozesuetan garrantzia handikoa da hori, objektu partikularretatik abiatuz (estentsiboak) objektu orokorrak definitzen direlako (intentsiboak).

Eredu dinamikoen adibideak

Jarduera matematikoan, oro har, eredu dinamikoak oinarrizko hiru testuingurutan erabil daitezke. Horiek dira:

• Esplorazioa. Enuntziatu baten edo problema matematiko baten hasierako baldintzak betetzen dituen eraikuntza bat diseinatzen da. Ondoren, hura erabiliko da sistemaren gaineko ondorioak ateratzeko.

• Ilustrazioa. Proposizio edo emaitza matematiko jakin bat simulatzen duen eraikuntza diseinatzen da. Erabiltzaileak ez daki zergatik den egia proposizioa, eraikuntzak ez du hori argitzen. Hala ere, ereduaren disposizio guztietan beteko da emandako proposizioa, eta egiaztapen induktibo gisa balio du. Eredu honek ilustratzeko balio du, baina inplementazio informatikoak ez ditu zertan jarraitu frogapenaren pauso formalak.

• Frogapena. Ilustratzeko erabili den eredua koloretsua eta bizia izan ohi da. Behin hura manipulatu ondoren, ikasleak bere burua konbentzitu du eta proposizioa egiazkoa dela “uste” du. Bigarren eredu bat erabili beharko da orain, frogapen formalaren pausoak jarraitzen dituena.

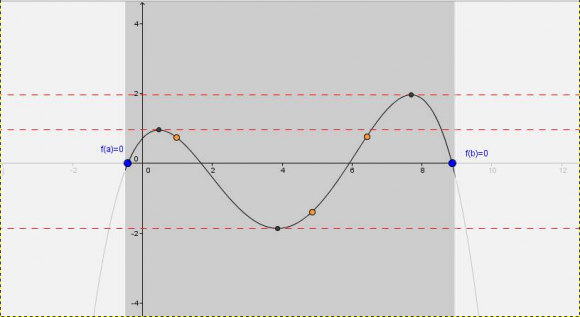
Rolleren Teorema

Eredu dinamiko baten adibide konkretua, hemen aurkituko duzue:

http://www.geogebratube.org/student/m71036

Aurrean duzun eraikuntza honek Rolleren Teoremaren enuntziatua betetzen du. Honenbestez, puntu urdinen eta laranjen posizioa nahi erara aldatuta ere, ezingo dituzu muturrak desagertu arazi.

Puntu urdinek tartearen muturrak adierazten dituzte. Une oro, funtzioa puntu laranjetatik pasako da.

Egileaz: Aitzol Lasa Oyarbide UPNA/NUPeko Matematika irakaslea da.

Sarrera honek #KulturaZientifikoa 1. Jaialdian parte hartzen du.