Ikasketa automatikorako sarrera gisa balio izan zuen artikuluan, ikasketa gainbegiratua aipatu zen. Bertan, makinari adibideak emateari buruz hitz egiten zen, makinak adibide horietatik eredu bat ikas zezan bere kasa. Ondoren, eredu hori erabiliz ikusi gabe zituen adibideak ongi sailkatzeko gai izango litzateke.
Saia gaitezen ordea hitz horietan dagoena askatzen. Lehenik eta behin, esan beharra dago ikasketa gainbegiratuan bi arazo mota aurki daitezkeela: aldagai jarraituak eta aldagai diskretuak. Blog honetan argitaratu zen Amazonek badaki artikuluan jada azaldu zen aldagai jarraituaren arazoa. Ez dugu berriro han esandako guztia errepikatuko. Ez. Artikulu haren amaieran airean utzitakoari helduko diogu oraingoan. Gogoratzen?
“Artikulu honetan ez dugu azaldu parametroak nola ikasten diren. Egia esanda, ikasketa prozesua ez da oso zaila. Deribatuak ulertuz gero, aise uler daiteke parametroak nola ikasten diren. Baina hori, agian, beste baterako utziko dugu.”
Iritsi da bada eguna! Gaur azalduko dugu erregresio lineala nola egiten den eta zergatik den ikasketa gainbegiratuaren adibide bat.
Arazoa planteatzen
Demagun etxebizitza ezberdinen prezioak asma ditzakeen programa bat egin nahi dugula. Prezioa aldagai jarraitu bat da, edozein balio har baitezake: 100.000, 120.000, 120.002, 782.345 eta abar. Beraz, gure arazoa aldagai jarraituen arazoa da argi eta garbi. Aldagai jarraituko arazo bat dugunean, konponbide errazena erregresio lineala erabiltzea da.
Noski, gure programak ezingo du etxebizitzaren prezioa asmatu ez badizkiogu datu batzuk ematen. Ezaguna da etxebizitza baten prezioak aldagai askorekin duela erlazioa: gela kopurua, azalera, kokapena eta urte kopurua, hala nola. Beraz, esan dezakegu, etxebizitzaren prezioa aldagai horien funtzio bat dela.
Har dezagun funtziorik sinpleena: zuzena. Lehen aipatu ditugun aldagaiei x1, x2, x3, x4 eta x5 izenak ematen badizkiegu, gure zuzenaren ekuazioa honokoa litzateke:
prezioa = θ0 + θ1 x1 + θ2 x2 + θ3 x3 + θ4 x4 + θ5 x5
Hor ikusten dituzuen θ horiek, zuzenaren parametroak besterik ez dira, hots, ze malda izango duen eta non moztuko dituen gure ardatzak. Ohartu zaretenez, bost aldagaien funtzio gisa definitu dugunez prezioa, gure zuzena 6 dimentsiotako espazio batean bizi da. Baina horrek ez digu axola. Guk nahi duguna da behin x aldagai guztien balioa dakigunean, zuzen horrek etxebizitzaren prezioa esan diezagun.
Zuzen horren parametroek (θ zenbakiak) guztiz alda dezakete etxebizitzaren prezioa. Beraz, gure programak θ balio horiek behar bezala asmatu behar ditu prezio fidagarri bat emateko. Nola egingo dugu hori? Ikasketa gainbegiratua erabiliz, noski.
Lehenik eta behin, etxebizitza pilo bat bilduko ditugu. Beraien gela kopurua, azalera eta abarren datuak jasoko ditugu. Datu horientzako etxebizitzak duen prezioa ere jarriko dugu. Datu horiek guztiak gure ikasketa programari pasatuko dizkiogu. Ohartu, azken batean, gure 6 dimentsiotako espazio berezi horretan puntuak jartzen ari garela, besterik gabe. Puntu horiek guztiak jartzen ditugunean, erregresio lineala aplikatuko dugu. Hots, puntu horietara ongien gerturatzen den zuzena kalkulatuko dugu.
Zuzenaren bila ikasiz
Baina nola egiten da hori? Dirudiena baino errazagoa da. Sinplifika dezagun arazoa eta gera gaitezen bi dimentsiorekin bakarrik. Demagun etxebizitza baten prezioa bere azalerarekin bakarrik dagoela erlazionatuta. Gure x aldagaia etxebizitzaren azalera da eta y aldagaia berriz etxebizitzaren prezioa. Jar ditzagun grafikoa batean orain arte bildu ahal izan ditugun adibideak, hots, (x, y) bikoteak. 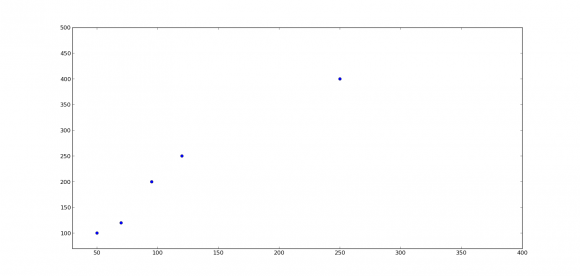
Hor duzue grafikoa. Datuak jarri ditugu 5 azalera balioentzako, 50 eta 250 metro koadroren artean. Orain, puntu horietara gehien gerturatzen den zuzena bilatu nahi dugu. Zuzen horren ekuazioa, y = θ0 + θ1x izango da eta ikasketa fasearen helburua θ zenbakien balio onena topatzea da.
Ikasketa algoritmoaren ideia nahiko sinplea da egia esan. Har ditzagun ausazko balio batzuk θ zenbakientzako eta ondorioz, kalkula dezagun zuzen bat ausazko balio horiekin. Ondoren, kalkula dezagun zuzen horren errorea bildu ditugun datuen aurka. Behin errorea kalkulatuta, aukera ditzagun balio berri batzuk θ zenbakientzako, gure zuzen berriaren errorea aurrekoa baino txikiagoa izan dadin. Eta jarrai dezagun prozesu horrekin errorea txikitu ezin den arte. Lortuko dugun zuzena, bildu ahal izan ditugun azalera-prezio balioetara ongien gerturatzen den zuzena izango da.
Prozesu horren giltzarria errorea minimizatzea da. Baina horretarako errorea nola definitu jakin beharko dugu, ezta? Demagun gure prozesuaren momenturen batean ondoko grafikoan azaltzen den zuzena lortu dugula: 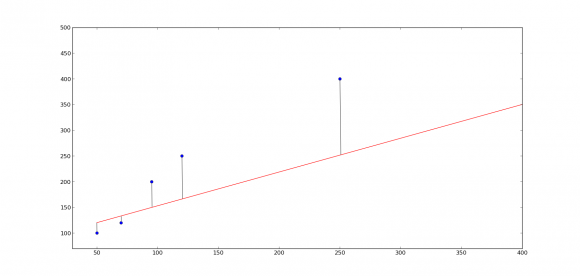 Zuzenaren errorea puntuekiko kalkulatzeko, bien arteko distantzia hartuko dugu, hots, (y’ – y), non y’ zuzenak aurreikusten duen prezioa den azalera batentzako eta y gure adibide puntuak ematen digun prezioa den. Baina errore guztiak positiboak izan daitezen (y’ – y)2 hartuko dugu errore baliotzat. Adibide puntu bakoitzaren errore koadratikoa hartu eta adibide kopuruarekin zatituz gero, batez besteko errorea kalkulatuko dugu, eta hori izango da zuzen baten errorea gure adibideekiko.
Zuzenaren errorea puntuekiko kalkulatzeko, bien arteko distantzia hartuko dugu, hots, (y’ – y), non y’ zuzenak aurreikusten duen prezioa den azalera batentzako eta y gure adibide puntuak ematen digun prezioa den. Baina errore guztiak positiboak izan daitezen (y’ – y)2 hartuko dugu errore baliotzat. Adibide puntu bakoitzaren errore koadratikoa hartu eta adibide kopuruarekin zatituz gero, batez besteko errorea kalkulatuko dugu, eta hori izango da zuzen baten errorea gure adibideekiko.
Ongi da. Baina nola minimiza dezakegu errore hori? Nola aukeratu behar ditugu hurrengo θ balioak? Beste behin, erantzuna matematiketan dago. Ohartu bazarete, gure erroreak karratuak dira. Hau da, zuzen posible guztien erroreak kalkulatuko bagenitu gure adibideen aurka, funtzio koadratiko bat izango genuke. Ikus dezagun hori hobeto beste grafiko batean:
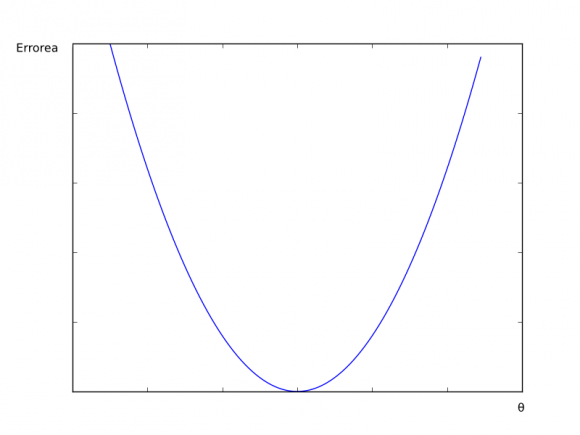 Hemen duzue gure zuzen guztien erroreen itxura, hots, errore balioak θ zenbaki guztientzako. Errorearen itxura horrelakoa izanik, argi dago guk bilatu nahi ditugun θ zenbakiak minimoan daudenak direla. Eta horretarako, lehen esan dugun prozesua jarraituko dugu. Prozesu horri gradiente jaitsiera deitzen zaio eta hurrengo grafikoan irudikatu dugu:
Hemen duzue gure zuzen guztien erroreen itxura, hots, errore balioak θ zenbaki guztientzako. Errorearen itxura horrelakoa izanik, argi dago guk bilatu nahi ditugun θ zenbakiak minimoan daudenak direla. Eta horretarako, lehen esan dugun prozesua jarraituko dugu. Prozesu horri gradiente jaitsiera deitzen zaio eta hurrengo grafikoan irudikatu dugu:
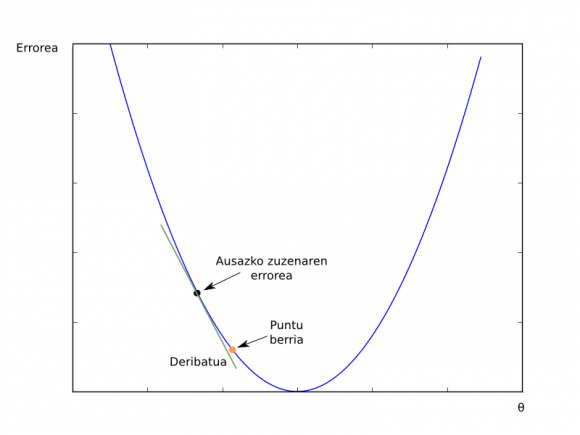 Bertan, puntu beltz gisa irudikatu dugu ausazko gure zuzena, ausazko θ balioekin kalkulatua. Ondoren, batxilergoan ikasi genuen deribatu ospetsua irudikatu dugu. Errorearen funtzioaren deribatuak gure ausazko θ balioetan kalkulatuta, ikusten duzuen zuzen hori ematen du emaitzatzat. Eta zuzen horrek, noranzko bat erakusten digu gainera. Kasu honetan, aldapa behera nola joan adierazten digu. Bada deribatuaren informazio hori erabilita, badakigu ze noranzko hartu behar dugun minimora gerturatzeko. Hori baliatuz, θ balio berriak kalkulatzen ditugu (irudian “Puntu berria”) eta berriro prozesua errepikatzen dugu errorea txikitu ezin den arte. Modu horretan, gure datuetara ongien gerturatzen den zuzena ikasi dugu. Eta zuzen horrek, edozein azalera baliorentzako prezio balio bat kalkulatuko digu.
Bertan, puntu beltz gisa irudikatu dugu ausazko gure zuzena, ausazko θ balioekin kalkulatua. Ondoren, batxilergoan ikasi genuen deribatu ospetsua irudikatu dugu. Errorearen funtzioaren deribatuak gure ausazko θ balioetan kalkulatuta, ikusten duzuen zuzen hori ematen du emaitzatzat. Eta zuzen horrek, noranzko bat erakusten digu gainera. Kasu honetan, aldapa behera nola joan adierazten digu. Bada deribatuaren informazio hori erabilita, badakigu ze noranzko hartu behar dugun minimora gerturatzeko. Hori baliatuz, θ balio berriak kalkulatzen ditugu (irudian “Puntu berria”) eta berriro prozesua errepikatzen dugu errorea txikitu ezin den arte. Modu horretan, gure datuetara ongien gerturatzen den zuzena ikasi dugu. Eta zuzen horrek, edozein azalera baliorentzako prezio balio bat kalkulatuko digu.
Ikasketa orokortuz
Ikusi berri dugun adibideak ikasketa prozesua modu sinple eta argi batean erakusteko balio izan digu. Dena dela, kontu egin azaldu ditugun kontzeptuak askoz arazo konplexuagoetara aplikatu daitezkeela. Adibidez, gure zuzenek nahi adina dimentsio izan ditzakete, hau da, prezioa aldagai askoren funtzioa izan daiteke. Bestalde, ez dugu ikasketa zuzenetara bakarrik mugatu beharrik. Erlazio ez-linealak ere ikas daitezke. Esaterako, prezioaren kalkuluan garrantzitsuak diren aldagaiak elkarrekin biderkatu ditzakegu eta aldagai konposatuak sortu. Modu horretara, gure ikasketa funtzioak edozein kurba ikas dezake (edozein erlazio aldagaien eta prezioen artean).
Erregresio lineala nahiko sinplea den arren, hainbat arazo praktikorentzako erabili izan da. Hala nola, epidemiologian, finantza eta ekonomiaren munduan, ingurugiro zientzietan eta Amazon bezalako dendetan erabiltzaileei produktuak aholkatzeko.
Sarrera honen asmoa ez zen ordea aplikazio eta detaile konplexu horietan sartzea. Ikasketa gainbegiratuaren ideia zabaldu nahi zen, adibide sinple batekin. Azken batean, irakurlea ohar dadin batxilergoan ikasitako oinarrizko matematikekin ordenagailu bat ikasten jarri dezakeela.
Egileaz: Gorka Azkune (@gazkune) informatikaria da eta DeustoTech-eko ikertzailea.
1 iruzkina
Gorka Azkunek, besteak beste, gaur egun adimen artifiziala du ikergai. Egiten ari den lanari buruz eta adimen artifizialari buruz hitz egin zuen Unibertsitatea.net atarian egin zioten elkarrizketan “Adimen artifizialean eta bere inguruko diziplinetan oso urruti gaude oraindik“.
Bestalde, informatika eta fisikako gaiak jorratzen dituzten hainbat artikulu eta lan argitaratu ditu azken urteotan euskaraz.