Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta aurten ere, udako oporretan egiteko astelehenero ariketa matematiko bat izango duzu, Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.
Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain, tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta irailean emaitza zuzenaren berri emango dizugu.
Hona hemen gure bosgarren ariketa: Korda neurtzen.
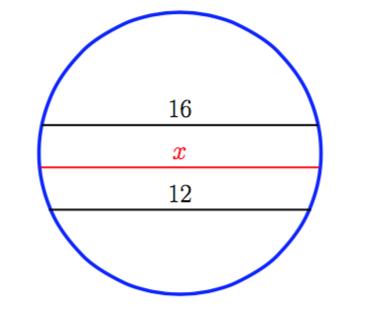
5) Zirkunferentzia bateko korda paralelo biren neurriak 16 cm eta 12 cm dira eta elkarren arteko distantzia 7 cm da. Zein da bietatik distantzia berera dagoen kordaren neurria?
Ariketak “Calendrier Mathématique 2019. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki daiteke.
3 iruzkinak
Eeee, honetan bakarrik esan dezaket:
Intuitzioak esaten dit 14 dela, 12 eta 16 artean erdibidean dagoen zenbakia baita. Baina ez dut ez formularik, ez ganorazko ezer intuitzio hori (zuzena ala okerra ikusiko dugu) laguntzeko. Geometrian uda honetan pot. XD
Ez dakit ondo ulertu dudan arazoaren mamia. Aspaldi ez nago matematikaren nomenklaturarekin eta ez nago oso seguru korda hitzaren esan nahiarekin. Pentsatzen det korda zirkunferentziaren perimetroren bi puntu lotzen dituen segmentua dela. Honela kordarik luzeena diametroa lirateke. Kasu honetan bi korda ditugu 16 eta 12 cm luzerakoak, elkarrekiko 7 cm ko distantziaz separatuta. Honela paralelogramo irregular bat osatuko dugu. Paralelogramo hau erditik mozten duen sektorearen luzera ebaztea besterik ez omen da. Nire kasuan Koldotxuk ateratzen duen neurri berdina ateratzen zait. (6+1)x2=14 cm.
Barkatu, baina lehen jarritako iruzkina okerra da. Kontuan hartu beharra dago zirkunferentzia batean sartuta daudela, honetarako erradioa eta zirkunferentziaren erdia ebatzi beharra dago. Pitagorasen teorema eta emandako datuekin ebatzi dezakegu;
R^2=(16/2)^2+h1^2
R^2=(12/2)^2+h2^2
28=h2^2-h1^2=(h2+h1)(h2-h1)
eta h1+h2=7 (enuntziatuak ematen digu datu hau)
Honetatik ateratzen dugu h2=5.5 eta h1=-1.5 (zirkunferentziaren erdia bi kordeen artean dago).
Zirkinferentziaren erradioa R=8.1394 ematen dit.
Berriro Pitagoras erabiliz, eta eskatzen zaigun korda azpiko kordatik 3.5 cm goruntz dagola jakinik (hauxe da erditik 2 cm azpiago) korda honen erradia 7.88 cm ateratzen zait eta bere korda 15.779 cm
Ea oraingoan ez dudan berriro hanka sartu.