Betidanik ezagutzen dira matematikarien ahalegin guztiei iskin egin dieten itxura errazeko galderak. Batzuetan mendeak joan dira eta jende askoren lana behar izan da norbaitek erantzuna lortu arte, Fermaten azken teorema lekuko. Beste batzuetan hor daude, zain. Galdera horietako bat aurkeztuko dizuet gaur, problema ireki ospetsuen artean enuntziaturik errazena duena seguruenik.
Collatzen aierua
Jokoa erraza da. Zenbaki arrunt bat hartuta, egizu ariketa hau:
- bikoitia bada, erdibitu;
- bakoitia bada, hirukoiztu eta bat gehitu.
Dei dezagun F agindu horiek definitzen duten funtzioa, hau da,
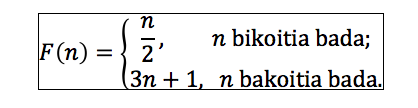
Orain egin beharreko lana hau da: zenbaki batekin hasita, egizu F funtzioak dioena; gero gauza bera lortutako zenbakiarekin, eta horrela behin eta berriro; ondoren, deskribatu lortzen den segidaren portaera. Segida horri hasierako zenbakiaren orbita edo hegaldia deritzogu. Ikus ditzagun zenbait adibide:
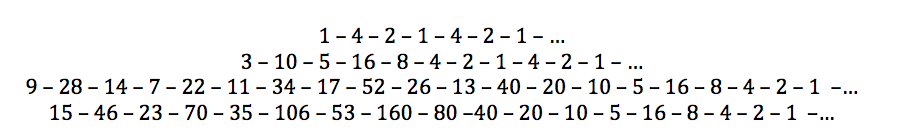
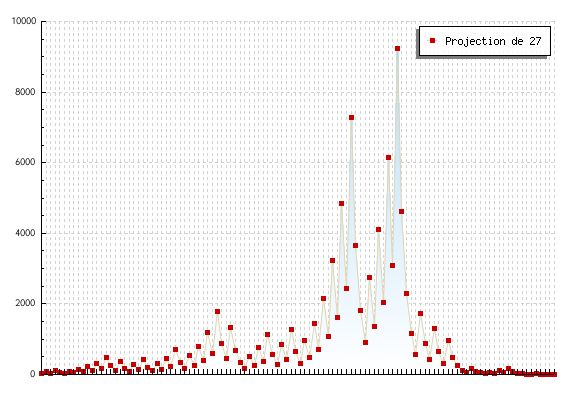
Orbita horiek guztiak 1 – 4 – 2 zikloa errepikatzera heldu dira, ikusten denez. Hasieran hartu ditugun balioek zerbait berezia ote dute? Utziko dizut, irakurle, zure gustuko aukerak egiten eta segiden bilakaera aztertzen. Adibide batzuk egin eta gero, ez baduzu oraindik probatu 27 zenbakia, egizu. Luze hartuko dizu, baina horren orbita ere 1 – 4 – 2 ziklora helduko da. Orduan —pentsatuko duzu— badut erantzuna: hasierako zenbakia edozein izanda ere, beti amaituko da berdin, 1 – 4 – 2 zikloan bueltaka. Baliteke, baina… inork ez daki oraindik! Horixe da, hain zuzen ere, problema honen magia, urte asko pasatu direla (80 inguru) norbaitek plazaratu zuenetik eta, bere xalotasunean, erronka handi bihurtu dela. Hori bai, denek uste dute baietz, ziklo horretan amaituko dela beti. Matematikan, ordea, uste izate hutsak ez du balio zerbait egiazkoa dela esateko, froga behar da, eta, hemen, ez daukagu. Bitartean, aieru bat baino ez da, espero den emaitza bat. Honela eman daiteke Collatzen aierua: edozein zenbakitatik hasita, orbita beti helduko da 1 – 4 – 2 ziklora.
Nori bururatu zitzaion? Matematikan problema honi loturik gehien aipatzen den izena Lothar Collatz (1910-1990) matematikari alemaniarrarena da, hari aitortzen baitiote problemaren jatorria, baina beste izen batzuk ere lotzen zaizkio: Ulam, Kakutani, Sirakusa… edo, besterik gabe, 3n+1 problema esan ohi da.

Ordenagailuen laguntza
Collatzen problema abiatu zenean ez zegoen ordenagailurik. Gaur egun, ordea, kalkulu-ahalmen izugarri handia dute makinek eta eskuz ezinezkoak diren kalkuluak egitea ahalbidetzen dute. Hortaz, geroz eta zenbaki handiagoak proba daitezke. Bada, 2017an egiaztatuta zegoen 20 zifra edo gutxiagoko zenbaki guztien orbitek aierua betetzen dutela, hau da, beti 1 – 4 – 2 ziklora heltzen direla. Hori bai, ordenagailuak ezin izango ditu inoiz zenbaki guztiak egiaztatu, infinitu baitira…
Zikloak
Zenbaki batean hasi eta bere orbitan berriro zenbaki bera lortzen bada, ziklo bat dela diogu, 1, 2 edo 4rekin hasita gertatzen den bezala. Ziklo horretan, hirugarren urratsean errepikatzen denez hasierako zenbakia, zikloaren luzera 3 da.
Besterik frogatu arte, hiru aukera teoriko daude orbita baterako:
- 1 – 4 – 2 ziklora heltzea;
- beste ziklo baten bueltan geratzea;
- infiniturantz joatea.
Existituko da beste ziklo bat? Ez da aurkitu, bestela ezetz erantzungo genioke aieruari eta problema beste modu batean formulatu beharko genuke. Baina ez da frogatu existitzen ez denik ere. Hori bai, badakigu horrelako ziklo bat egonez gero, haren luzera 17 000 000 000 (hamazazpi mila milioi) baino handiagoa izan beharko litzatekeela.
Gelditze-unea
Problemari erantzuna emateko nahikoa izango litzateke hau frogatzea: orbita batek beti hartzen du hasierako zenbakia baino balio txikiago bat, salbu 1ekin hasten bada. Utziko dizut, irakurle, zure kabuz pentsatzen zergatik horrek aierua frogatzen duen. Emaitza hori ere ez dugu ezagutzen, beraz. Zenbaki baten gelditze-unea esaten zaio bera baino txikiago den batera heltzeko behar den urrats-kopuruari. Ikus goiko adibideak: 3ren gelditze-unea 6 da (seigarren urratsean 2 dugu), 9rena 3 (hirugarren urratsean 7) eta 15ena 11 (hamaikagarren urratsean 10). 27ren orbita kalkulatzeko astia hartu baduzu, ikus zenezake gelditze-unea 96 dela, orduan lortzen baita 23 (27 baino txikiago den lehena). Hortaz, problemaren beste formulazio bat hau litzateke: frogatu zenbaki guztiek gelditze-une finitua dutela.
Erabateko gelditze-unea da 1era heltzeko behar den urrats-kopurua. Lehengo adibideetara itzulita, 3rena 7 da, 9rena 19 eta 15ena 17. Berriro 27 zenbakiak marka handia jartzen du, 111 urrats behar baititu 1era heltzeko. Bistan da zenbaki handiago batekin hasteak ez duela esan nahi gelditze-unea edo erabateko gelditze-unea handiagoa izango dela. Ordenagailuetarako erronka handia da emandako gelditze-une bat duten balioak kalkulatzea. Esaterako, erabateko gelditze-unea zehazki 2000 duen zenbaki txikiena aurkitzea izan zen mende hasierako erronka eta ez zen lortu 2008ra arte; 17 zifrako zenbaki bat da.
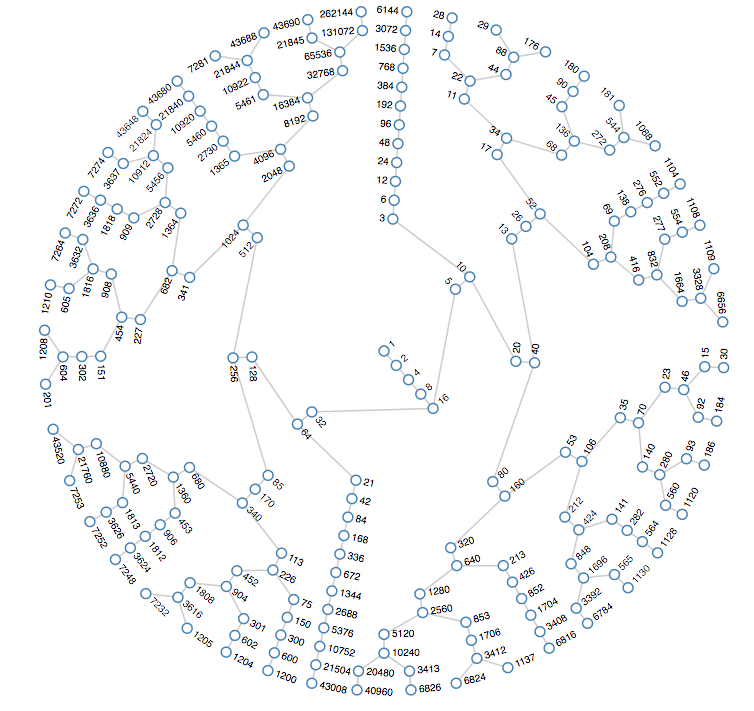
Erlazionatutako emaitzak
Besterik ezean, ohikoa izaten da matematikan tarteko emaitzen bila joatea. Problema honetarako, itxura probabilistikoa duten emaitzak daude, adibidez. Hitz arruntetan, “aierua ia zenbaki guztietarako betetzen da” esaten dute emaitza horiek. Matematikan “ia guztiak” horrek formulazio zehatz bat behar du. Hona hemen horietako bat. Finka dezagun N zenbakia. Izan bedi b(N) N baino txikiago diren zenbakietatik gelditze-une finitua dutenen kopurua. Aierua egia bada, denak izango dira, baino hori ez dakigu. Bada, frogatuta dagoena da b(N)/(N-1) proportzioaren limitea 1 dela N infiniturantz doanean. Hori urrun dago espero dugun emaitzatik, baina aieruaren egiazkotasunaren aldeko urrats bat da.
5n + 1 aldaera
Demagun n zenbaki bakoitia 3rekin biderkatu beharrean 5ekin biderkatzen dugula, hau da, 5n+1 egiten dugula. Bikoitiak, lehengo moduan, erdibitu egingo ditugu. Ikus ditzagun orbita batzuk:
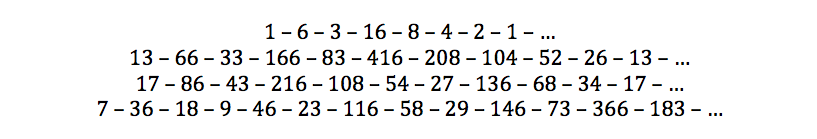
Lehen hirurak zikloak dira (5etik hasita bigarren zikloan amaituko dugu). Laugarren adibidea, 7tik hasten dena, hamabigarren urratsean gelditu dugu, ziklo batera heldu barik. Luza dezakegu orbita, baina ez dirudi itzultzen denik, eta bai, ordea, zenbaki handietara iristen dela. Horrek iradokitzen du 7ren orbitak infiniturantz joko duela. Hori ere problema irekia da, inork ez baitaki hala den edo ez. 3n+1 problemari aldaketa txikia egin badiogu ere, eragin handia du orbiten dinamikan.
Ariketa (erraz) bat irakurlearentzat
Har ezazu beste funtzio hau:
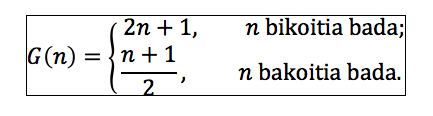
Azter ezazu hasierako balio bakoitzarentzat zein den eboluzioa. Aurrekoen aldean, orain askoz errazagoa da azaltzea zein den orbiten portaera. Hau ez da problema irekia, noski. Anima zaitez erantzuna bilatzen.
Gehiago jakiteko
- Shalom Eliahouren hiru artikuluko sorta bat: lehenak oinarriak azaltzen ditu; bigarrenak frogatzen du zergatik ez dauden 5 luzerako zikloak; hirugarrenak luzera handiagoko zikloak aztertzen ditu.
- Jean-Paul Delahayeren artikulu bat Pour la Science aldizkarian (74. dosierra, 2012, 98-103 or.).
- Eric Roosendaalen webgune berezia: On the 3n+1 problem.
- Norbere gustuko zenbakia sartu eta gelditze-unera arteko orbita edo orbitaren propietateak ematen dituzten online aplikazioak:
- http://www.numbertheory.org/php/3x+1.html;
- http://l.pellegrino.free.fr/syracuse/index.php;
- http://ahonga.fr/js/syracuse_3n+1.html.
- Jason Daviesek sorturik, 18 urrats edo gutxiagotan 1era heltzen diren zenbakien grafikoaren eraikuntza.
Egileaz: Javier Duoandikoetxea Analisi Matematikoko Katedraduna da UPV/EHUn.