Erantzun asko eta gehienak zuzenak izan ditugu aurten. Eskerrik asko denoi parte hartzeagatik.
Zenbaki baten zifren biderkadura 18900 da. Zein da propietate hori duen zenbakirik txikiena?
18900 = 2 x 2 x 3 x 3 x 3 x 5 x 5 x 7 denez, faktore horiek guztiak agertu beharko dira gure zenbakiaren zifretan. Eta nahi beste bider jar dezakegu 1 zifra, baina horrela zifra kopurua handituko genuke eta ez genuke eskatzen den zenbakirik txikiena lortuko.
Faktore guztiak dauden moduan idatzita, edo ordena aldatuta, zortzi zifrako zenbakia genuke. Zifra gutxiago erabiltzeko, 2 eta 2 idatzi ordez, 4 jar dezakegu. Era berean, 2 eta 3ren ordez, 6; edo 3 eta 3ren ordez, 9. Horren bitartez, sei zifrako zenbakia lor dezakegu, baina ez zifra gutxiagokoa.
Eskatzen zaigun zenbakirik txikiena lortzeko, 2 zifra mantentzea komeni zaigu. Horrela, 2, 6, 9, 5, 5 eta 7 izango dira gure zenbakiaren zifrak. Txikiena lortzeko, txikitik handira ordenatuko ditugu: 255679.
Denda batean gozoki batek 5 zentimo balio du. Eskaintza bat jarri dute: 35 gozokitik behera erosiz gero, %5eko deskontua egiten dute; 36 eta 55 gozoki artean, %12koa; eta 56 gozokitik gora, %20koa. Lehen erosketan %5eko deskontua egin digute, eta bigarren erosketan, %12koa. Dena batera erosi izan bagenu, %20ko deskontua lortuko genukeen eta 39 zentimo aurreztu. Zenbat gozoki erosi ditugu?
Lehenengo aldian m gozoki erosi baditugu, 5m-ren %95 ordainduko dugu. Bigarren aldian n gozoki erosita, 5n-ren %88. Dena batera erosi izan bagenu, 5(m + n)-ren %80 ordainduko genuen, 39 zentimo gutxiago. Beraz,
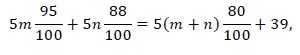
edo 15m + 8n = 780. Hemendik, 8n = 780 -15m = 15 (52 – m) ateratzen dugu. Hortaz, 8n 15en multiploa da, eta horretarako, n izan behar da 15en multiploa. Gainera, 36 eta 55 artean egon behar denez, n = 45 da aukera bakarra. Horrek m = 28 dakar. Denetara, 73 gozoki erosi ditugu.
1, 2, 3, 4, 5, 6 eta 7 digituak errepikatu barik erabiliz idatz daitezkeen zazpi zifrako zenbaki guztiak txikitik handira ordenatu ditugu. Zer tokitan dago 3654712 zenbakia zerrenda horretan?
Aurretik egongo dira 1 edo 2 hasieran duten guztiak. Bakoitzetik 6! = 720 zenbaki, sei zifraren artean aukeratu behar baitugu jarraipena. Aurretik baita ere 31, 32, 34 eta 35 hasierakoak, bakoitzetik 5! = 120. Gero, 361, 362 eta 364 hasierakoak, 4! = 24 bakoitzetik. Ondoren, 3651 eta 3652 hasierakoak, 3! = 6 bakoitzetik. Azkenik, 36541 eta 36542 hasierakoak, 2 bakoitzetik. Denetara,
2 x 720 + 4 x 120 + 3 x 24 + 2 x 6 + 2 x 2 = 2008
dira aurretik dituen zenbakiak. Beraz, 2009. lekuan egongo da.
Maren eta Miren pista zirkular batean korrika hasi dira, bakoitza diametro baten mutur batean. Abiadura konstantea mantentzen dute, nork berea, eta elkarren kontrako noranzkoan doaz. Lehen aldiz gurutzatzen direnean, Marenek 100 metro egin ditu. Une horretatik aurrera, Mirenek 150 metro egin dituenean gurutzatu dira berriro. Zein da pistaren luzera?
Lehen soluziobidea. Pista erdiaren luzera l bada, Marenek 100 metro egin ditu eta Mirenek l – 100 metro. Hurrengoan elkartzen direnerako, Marenek 2l – 150 metro eta Mirenek 150 metro. Abiadura konstantean egiten dutenez, distantziak proportzionalak izan behar dira:
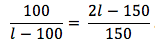
Ekuazio horren soluzioak l = 0 (baliogabea) eta l = 175 dira. Pistaren luzera 350 metrokoa da.
Bigarren soluziobidea. Gehienok ekuazioen bide hori hartuko genuke, seguruenik, baina Joseluk modu erraz eta dotorean ebatzi du problema. Abiadura konstante mantentzen dutenez, pista osoa egiteko bien artean, pista erdia egiteko behar dutenaren bikoitza da. Hortaz, pista osoaren 200 metro egingo ditu Marenek (erdian 100 egin dituelako) eta 150 metro Mirenek. Bien artean, 350 metro. Horixe da pistaren luzera.
ABC triangelu aldeberdina da eta M, BC aldeko puntu bat. M puntutik BC aldearen zuzen perpendikularrak P puntuan ebakitzen du AC aldea eta Q puntuan AB aldearen luzapena. Izan bedi N, MQ zuzenkiaren erdiko puntua. Baldin PC = 2 cm eta BN = 7 cm badira, zenbat da BC aldearen luzera?
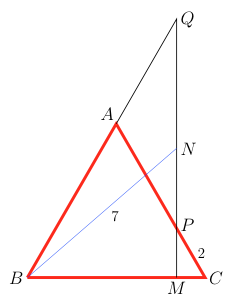
Izan bedi l triangeluko aldearen luzera. Triangelu aldeberdinaren angeluak 60 gradukoak dira. CMP triangeluan CP = 2 denez, MC = 1 da. Orduan, BM = l – 1 izango da eta BMQ triangeluari begiratuz, MQ = (l – 1) √3 izango da. MN = MQ/2 denez, Pitagorasen teorema erabiliko dugu BMN triangeluan:
![]()
Hortik,
![]()
Eta Gutxi gorabehera, 6.2915 da.
Ehun karta ditugu 1etik 100eraino zenbakituta. Hiru kartako multzoak egin nahi ditugu propietate honekin: hirukoteko karta baten zenbakia beste karta bien zenbakien biderkadura da. Zenbat multzo egin daitezke gehienez? (Ezin dira kartak errepikatu, noski.)
Hirukote bakoitzak derrigorrez behar du 10 baino txikiago den karta bat. Bestela, edozein zenbaki biren biderkadura 100 baino handiagoa izango litzateke, eta ezin izango genuke hirugarren karta aukeratu. Gainera, ezin da 1 zenbakia egon, horrek bi zenbaki berdin beharko lituzkeelako. 2tik 9rainoko zenbaki bakoitza hirukote desberdin batean sartuz gero, zortzi hirukote lortuko genituzke eta hori izango litzateke kopuru handiena. Eta bai, egin daitezke zortzi, modu askotan. Esate baterako,
(9,10,90), (8,11,88), (7,12,84), (6,13,78), (5,14,70), (4,15,60), (3,16,48), (2,17,34).
Beraz, zortzi multzo egin daitezke gehienez.
Iñakiren erantzunaren arabera, esango nuke hirukote posible guztiak hartu dituela, hirukote batetik bestera kartak errepikatu arren. Horiek zenbatu nahi izanez gero, bide hau segi dezakegu. Hirukoteko karta txikiena 2 bada, 48 aukera daude (hurrengo karta 3 eta 50 artean egon daiteke); txikiena 3 bada, 30 aukera (hurrengoa 4 eta 33 artean); txikiena 4 bada, 21 aukera (hurrengoa 5 eta 25 artean); eta horrela, txikiena 9 izan arte, 2 aukera (hurrengoa 10 edo 11). Denetara, 137 hirukote ateratzen dira.
Egileaz:
Javier Duoandikoetxea Analisi Matematikoko Katedradun erretiratua da UPV/EHUn.