Aurten ere erantzun asko izan ditugu eta gehienak zuzenak. Eskerrik asko parte hartu duzuen guztioi.
Mahai-joko batean animaliak erosten dira. Behi batek 5 euro balio du, txerri batek 1 euro eta 20 txorik ere 1 euro. Gutxienez bakoitzetik bat erosita, 100 animalia erosi ditugu, 100 euro ordainduta. Zenbat txori erosi ditugu?
Esan dezagun x behi, y txerri eta z txori erosi ditugula. Orduan,
x + y + z = 100 eta 5x + y + z/20 = 0.
Bigarren ekuazioari lehena kenduz,
4x – 19z/20 = 0 edo 80x – 19z = 0.
Ezin direnez x eta z 0 izan, 100 baino txikiago den soluzio bakarra x = 19 eta z = 80 da. Hortik y = 1 ondorioztatzen da. Beraz, 19 behi, txerri bat eta 80 txori erosi ditugu.
Beste bide bat hartu nahi izanez gero, kontuan izan prezioa zenbaki osoa denez, txori kopurua 20ren multiploa dela, hots, 20, 40, 60 edo 80 txori erosi ditugula. Banan-banan probatuz, bakarrik 80 txoriren kasuak ematen du soluzio osoa behientzat eta txerrientzat.
Irudiko zuzenki batzuen neurriak hauek dira: AB = 9 cm, BC = 14 cm, CD = 13 cm, DA = 12 cm eta BD = 15 cm. Zein da PQ zuzenkiaren neurria?
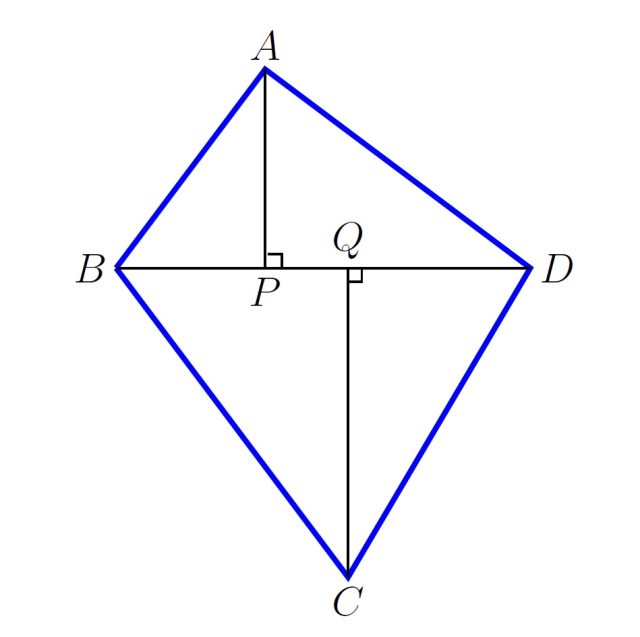
Pitagorasen teorema erabiliz ABP eta APD triangeluetan,
AP2 = AB2 – BP2 = AD2 – PD2.
Idatz dezagun BP = x. Orduan, PD = 15 – x da eta
92 – x2 = 122 – (15 – x)2.
Hortik, x = 5.4 cm ateratzen da.
Era berean, BCQ eta CDQ triangeluak erabiliz,
CQ2 = BC2 – BQ2 = CD2 – QD2.
QD = y idatziz, BQ = 15 – y da, eta
142 – (15 – y)2 = 132 – y2.
Hortik, y = 6.6 cm.
Beraz, PQ = 15 – 5.4 – 6.6 = 3 cm.
Zenbaki arrunt bati ezkerreko lehen zifra ezabatuta lortzen den zenbakia aurrerakoaren 29rena da (aurrekoa zati 29). Zein da propietate hori duen zenbakirik txikiena?
Zenbaki arrunt baten forma orokorra hau da: 10ka + N, non a lehen zifra den eta N k zifrako zenbaki bat. Adibidez, 4138 = 103 x 4 + 138. Ariketak diosku 10ka + N = 29N dela, hau da,
10ka = 28 N = 4 x 7 x N.
Ezkerreko atala 7ren multiplo izateko, a izan behar da 7ren multiplo, beraz, a = 7. Hortik, 10k = 4N ateratzen da eta k gutxienez 2 izango da, 10k 4ren multiplo izan dadin. Beraz, 100 x 10k-2 = 4N, hots, 25 x 10k-2 = N dugu.
Txikiena, k = 2rako, N = 25 da. Ondorioz, ariketaren soluzioa 725 da.
Propietatea betetzen duten zenbaki guztiak hauek dira: 725, 7250, 72500, 725000…
Aurkitu zenbaki arrunten (a, b, c) hirukote guztiak ekuazio hauek betetzen dituztenak:
ab + bc = 44, ac + bc = 23
Bistan da b eta c ezin direla 0 izan, eta a = 0 balitz, ekuazioak ez lirateke bateragarriak izango (bc = 44 eta bc = 23 izango genuke aldi berean).
Bigarren ekuazioa (a+b) c = 23 idatzita, a + b = 23 eta c = 1, edo a + b = 1 eta c = 23 izan behar dira. Azken aukera hori ezinezkoa da, a + b gutxienez 2 delako, beraz, a + b = 23 eta c = 1 ditugu. b = 23 – a eta c = 1 lehen ekuaziora eramanez, a2 – 22a + 21 = 0 bigarren mailako ekuazioa lortzen dugu. Horren soluzioak a = 1 eta a = 21 dira. Hortaz, bilatzen ditugun hirukoteak (1, 22, 1) eta (21, 2, 1) dira.
1 eta 7 arteko zifrak errepikatu gabe erabilita idatz daitezkeen zenbaki arrunt guztietatik, 10.000 baino txikiago direnen artean, zenbat dira 15en multiplo?
Zenbaki bat 15en multiplo izateko, 3ren eta 5en multiplo izan behar da. 5en multiplo izateko, azken zifra 0 edo 5 izan behar da. Hemen azken zifra 5 izango da, ezin dugulako 0 erabili. 3ren multiplo izateko, zifren batura 3ren multiplo izan behar da. Azken zifra 5 denez, horren aurrekoen batura 1, 4, 7, 10, 13 edo 16 izango da (19 edo gehiago izatea ezinezkoa da).
Zifra biko zenbakiak: 15, 45 eta 75.
Hiru zifrako zenbakiak: 135, 165, 345, 375, 465 eta 675, gehi lehen bi zifrak trukatuz lortzen diren beste seiak. Denetara, 12 zenbaki.
Lau zifrako zenbakiak: 1245, 1275, 1365, 2475, 3465 eta 3675, gehi lehen hiru zifrak permutatuz lortzen diren guztiak. Hiru zifren permutazioek 6 aukera ematen dituztenez, denetara 36 zenbaki lortuko ditugu.
Guztira, 3 + 12 + 36 = 51 zenbakik betetzen dute eskatutako baldintza.
Egurrezko ABC triangelua dugu mahai gainean. C erpineko angelua 25º-koa da. Triangelua birarazi dugu, B erpina finkatuta, A’BC’ posiziora heldu arte, non A’, B eta C lerrokatuta dauden. Hori egin dugunean, C, A eta C’ ere lerrokatuta geratu dira. Zein da B erpineko angeluaren neurria?
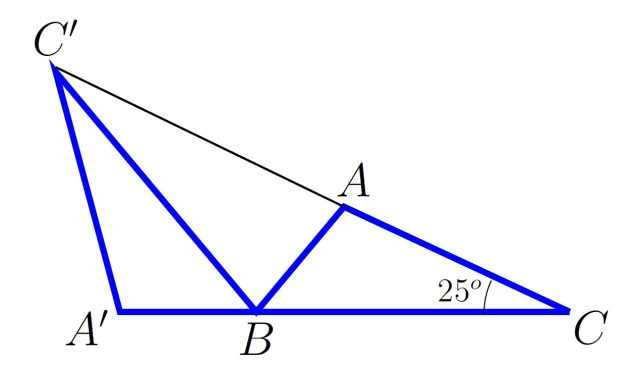
Lehenengo eta behin, kontura gaitezen ABC eta A’CC’ triangeluen angeluak berdinak direla. Izan ere, C erpineko angelua bietan dago, eta A eta A’ erpinetako angeluak berdinak dira eraikuntzagatik. Hortaz, hirugarren angelua ere berdina da, eta bilatzen dugun angelua A’CC’ triangeluaren C’ erpineko angeluaren berdina da.
Bestalde, BCC’ triangelua isoszelea da, BC = BC’ delako. Orduan, ang(BC’C) = ang(BCC’) = 25oda. Gainera, ang(A’C’B) = 25oda eraikuntzagatik. Beraz, ang(A’C’C) = 50oda, eta hori da eskatutako angeluaren neurria.
Egileaz:
Javier Duoandikoetxea Analisi Matematikoko Katedradun erretiratua da UPV/EHUn.
1 iruzkina
Eskerrik asko zuri, Javier, hau guztia posible egiteagatik!