Edward Page Mitchell (1852-1927) kazetari estatubatuar bat izan zen. Aintzatespen berezia jaso zuen New Yorkeko The Sun egunkarian argitaratu zituen zientzia-fikziozko kontakizunengatik. Hain zuzen, egunkari horretako editore burua ere izan zen, 1926an erretiroa hartu zuen arte. 1973an haren lehenengo 30 narrazioen antologia bat argitaratu zen (1874-1886), The crystal man izenburupean. Izenburu hori bat zetorren bere kontakizun iradokitzaileenetako batekin, ikusezintasunari buruzkoa, zeina 1881ean argitaratu baitzen, H.G. Wellsen eleberri ospetsua argitaratu baino 16 urte lehenago.
Mitchellen istorioetako hamar gaztelaniara itzulita argitaratu ziren. Istorio horietan, gizaki ikusezinaz gain, beste gai batzuk ere lantzen dira, hala nola denboran zeharreko bidaiak, garun artifiziala (Babbageren makina analitikoa baino hobea) eta teleportazioa. Zientzia-fikziozko hamar kontakizun bikain horietatik nire gustukoenak ez dauka zerikusirik gaur egun oker aipatu ohi diren balizko teknologia kuantikoekin edo AA penagarriarekin. Takiponpoa da.
Takiponpoa (El Taquipompo)
Maitemindutako bikote batek ezkontzeko baimena eskatzen du, baina oztopo handi bat dago: emaztegaiaren familia matematikari familia entzutetsua izanik, senargaiak bertan sartzea merezi duela erakutsi behar du. Kontakizunaren xehetasun gehiago hemen aipatu gabe –izugarri gomendatzen dut kontakizun osoa irakurtzea–, jarraian tramankulu protagonistaren ebazpen matematiko eta fisikoetako batzuk azalduko ditugu.
Objektuak azkar garraiatzeko lurra, itsasoa edo airea erabili behar ditugu, eta energia asko gastatu. Askoz ere eraginkorragoa eta azkarragoa da takiponpoa, eta ez du energiarik gastatzen. Nola funtzionatzen du takiponpoak Lurrean?
Kalkuluak egiteko, fisikarioi hipotesi sinplifikatzaileak ezartzea gustatzen zaigu, hutseko behi esferikoa kasu. Oraingoan imajinatuko dugu zulo bat egin dezakegula Aucklandetik (Zeelanda Berria) Rondara (Espainia). Hiri horiek elkarren antipodak direnez, eta ustez behintzat gure planeta esfera bat denez, tunela Lurraren erditik igarotzen da. Suposatuko dugu, halaber, Lurraren dentsitatea konstantea dela eta zuloari aire guztia kentzen diogula. Horixe da takiponpoa, 1. irudian ikus daitekeen moduan.
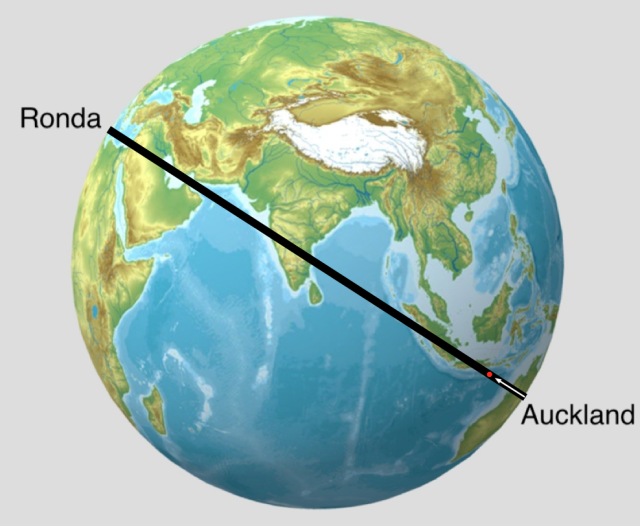
Nola funtzionatzen du?
Aucklandetik Rondara premiazko bidalketa bat egin behar badugu, paketea zuzenean zulotik bota dezakegu. Grabitazio unibertsalaren legearen arabera, planetatik kanpoalderantz grabitate indarra alderantziz proportzionala da distantziaren karratuarekiko, baina zer gertatzen da tunelaren barruan bidali dugun pieza erortzen den bitartean? Kalkuluak ez dira zailak, baina ezta azalekoak ere; izan ere, azelerazioa ez da konstantea, objektutik Lurraren erdigunera dagoen distantziaren araberakoa baizik.
Gaussen legea grabitate eremuari aplikatzen badiogu eta objektutik Lurraren erdigunerako distantziaren baliokide den erradioa duen esferaren bolumena kalkulatzen badugu, frogatu dezakegu azelerazioa (eta objektu horren gaineko indarra) jaitsi egiten dela Lurraren erdigunerako distantzia jaisten den heinean, modu linealean. Hori horrela, oso erraza da takiponpoaren bidez bidali dugun gorputzaren gaineko indarraren proportzionaltasun konstantea kalkulatzea, zeina planetaren dentsitatearen eta grabitazio unibertsalaren konstantearen araberakoa baita.
2. irudian Lurrak objektuaren gainean eragiten duen grabitazio indarra irudikatu dugu, izan tunelaren barruan zein kanpo espazioan. Benetako aldaketa planetaren gainazalean gertatzen da. Takiponpoaren barruan distantziarekiko proportzionala den indar hori Hookeren legearen arabera malgukiek jasaten dutenaren berdina da, eta horrek adierazten digu Lurrak malguki batek bezalaxe erantzuten duela.
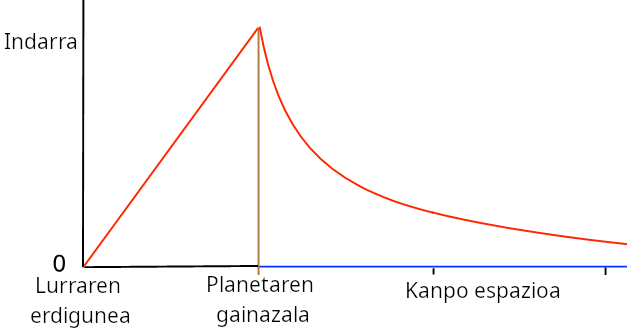
Fisikarioi asko gustatzen zaizkigu malgukien balantzetan, musika tresnetan eta askotariko uhinetan agertzen diren osziladore harmonikoak, eta unibertso osoa horien bidez azaldu nahi izaten dugu. Hori takiponpoaren kasu xumeari aplikatuta, adieraz dezakegu Aucklandetik Rondara bidalitako premiazko paketea linealki beheranzkoa den azelerazioarekin eroriko dela Lurraren erdigunera, erdiko puntua goreneko abiaduran igaroko duela eta modu simetrikoan iritsiko dela Rondara. Rondan paketea jasotzen ez badugu, berriz ere eroriko da eta Aucklandera iritsiko da, eta ez du batere energiarik behar izango joan-etorri osoan.
Takiponpoaren zifrak Lurrean
Zenbat denbora behar da paketea herri batetik bestera iristeko? Kalkulu integral erraz bat eginda –grabitazio unibertsalaren konstantea G (6,67 10-11 N m2/kg2) eta Lurraren dentsitatea (5520 kg/m3) erabiliz–, ondoriozta dezakegu takiponpoak 2530 segundo besterik ez dituela behar paketea helmugara eramateko, hau da, 42 minutu pasatxo; eta berdin dio paketea arina edo astuna izan.
Mugimendu harmoniko sinpleari aplikatuta, denbora hori oszilazio aldiaren erdia da; horrenbestez, mugimendu harmoniko horren periodoa T=5060 segundo da (joan-etorria). Oszilazio horren maiztasuna, Hertzetan (HZ), periodoaren alderantzizkoa da.
Takiponpoa gaur egungo garraiobideetako edozein baino askoz ere azkarragoa da. Tramankuluak Lurraren erdigunean hartzen duen abiadura gorena kalkulatuta, ondoriozta dezakegu 7910 m/s-koa dela edozein pakete bidalita ere, eta ez du ez erregairik ez elektrizitaterik behar. Espero dugu aurkikuntza hori nahikoa izana Edward P. Mitchellen kontakizuneko bikote zoriontsuak ezkontzea merezi duela erakusteko.
Erreferentzia bibliografikoa:
- Sam Moskowitz (Ed.) (1973). The Crystal Man: Stories by Edward Page Mitchell. Doubleday Science Fiction ISBN: 978-0385031394
- Edward Page Mitchell (2015). El espectroscopio del alma. Orciny Press ISBN: 978-8494318115
Egileaz:
Víctor Etxebarria Ecenarro Bilboko Juan Crisóstomo Arriaga Kontserbatorioan diplomatutako luthierra da, eta Sistemen Ingeniaritzako eta Automatikako katedraduna da Euskal Herriko Unibertsitatean (UPV/EHU).
Jatorrizko artikulua Cuaderno de Cultura Científica blogean argitaratu zen 2024ko urriaren 27an: El muelle de la Tierra.
Itzulpena: UPV/EHUko Euskara Zerbitzua.