Erantzun guztiak zuzenak izan dira. B=A+11 eta B2=A2+1001 behar direnez, A=40 eta B=51 lortzen dira.

Julenen erantzuna zuzena da. Iñakiren erantzunean, 11 eta 18 elkarrekin trukatuta daude. Honela geratzen da taula:

Ekhik du arrazoia eta ez Julenek. Toki bakoitietan dauden zifren baturari toki bikoitietan dauden zifren batura kenduta, 11ren multiploa lortu behar da (ez du zertan 0 izan). Hortaz, 9, 7 eta 1 doaz leku bakoitietan (6 aukera), eta 2 eta 4 toki bikoitietan (2 aukera). Denetara, 12 dira. Ekhik zerrenda osoa eman digu, gainera.

Zuzen daude Luis Pedriniren eta Iñakiren erantzunak. Zirkulu txikiaren erradioa handienaren 2/3 da. Horren ondorioz, txikiaren azalera handienaren (2/3)2 da, hots, 4 cm2. Hona hemen bide bi erradioen erlazioa arrazoitzeko.
Lehen bidea:

ANM triangelua zuzena da (erradioa eta zuzen ukitzailea perpendikularrak dira). NAM angelua 30o-koa da, beraz, AM=2NM. Eta NM=MB denez, MB=AB/3.
Bigarren bidea:
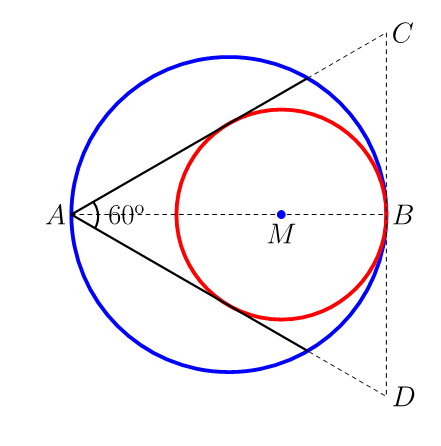
ACD triangelua aldeberdina da. M triangeluaren zentroa da. Beraz, MBren luzera AB altueraren 1/3 da.
Iñakiren erantzuna zuzena da.
Izan bedi x kirol bakarra egiten dutenen kopurua. Orduan, 78-x dira kirol bi egiten dutenak. Hortaz,
49 x + 80 (78 – x) = 1198 + 1269 + 1572 = 4039.
Hortik ateratzen dugu 71 direla kirol bakarra egiten dutenak eta 7 kirol bitan ari direnak.
Orain arloka jarraitu behar dugu. Izan bitez a1 atletismoa bakarrik egiten dutenak eta a2 atletismoaz gain beste arlo batean ari direnak. Orduan,
49 a1 + 40 a2 = 1198.
Ekuazio honek soluzio osoak behar ditu. Baturaren azken zifra 8 izan dadin, a1 = 2, 12, 22… izan beharko da. Erraz ikusten da a1 = 22 eta a2 = 3 direla.
Era berean, b1 badira igeriketa bakarrik egiten dutenak eta b2 igeriketa eta beste arlo bat,
49 b1 + 40 b2 = 1269.
Orain, b1 = 1, 11, 21… Hortik, b1 = 21eta b2 = 6 lortzen dira.
Azkenik, c1 badira txirrindularitza bakarrik egiten dutenak eta b2 txirrindularitza eta beste kirol bat,
49 c1 + 40 c2 = 1572.
Orain, c1 = 8, 18, 28… eta, ondorioz, c1 = 28 eta c2 = 5 lortzen dira.
Galderaren erantzuna hau da: 25 atletismoan, 27 igeriketan eta 33 txirrindularitzan.
Oharra.- Berez, hasieran egin dugun kalkulua (zenbat ari diren kirol bakarrean eta zenbat bitan) ez da inon behar. Areago, ariketak ez balu esango 78 bazkide direla ere, lortu dugun soluzioa da posible den bakarra eta bazkide-kopurua 78 dela ondorio modura aterako genuke.
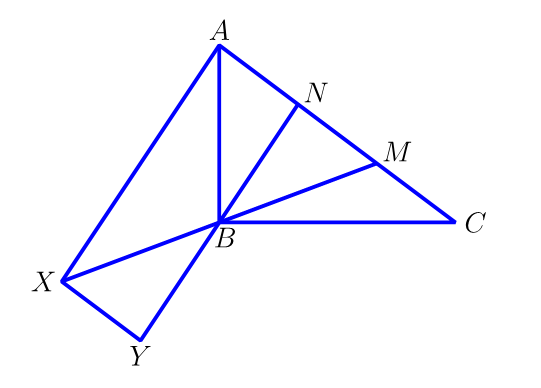
Iñakik lortu duen azalera zuzena da, 32 cm2, baina arrazonamendua ez da zuzena, ez baitago arrazoirik AC=AX izan dadin. Nahikoa litzateke irudia deformatzea horretaz konturatzeko.
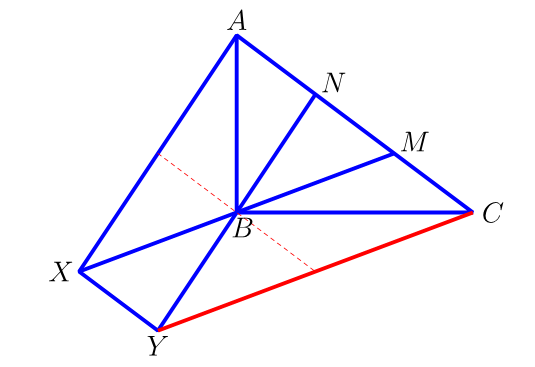
AN=NM=MC denez, ANB, NMB eta MCB triangeluek azalera bera dute, 4 cm2. XB=BM eta YB=BN direnez, NMB eta XYB triangeluak berdinak dira eta, gainera, NM eta XY paraleloak dira. Orduan, AXYN eta XYMC paralelogramoak dira. Ondorioz, irudiko triangelu guztien azalera 4 cm2 da. Denetara, 32 cm2.
Beste modu batez arrazoituta: AXM triangeluan, XB=BM denez, XBA eta ABM triangeluek azalera bera dute, 8 cm2, beraz. Era berean, CYN triangeluari begiratuz, YBC eta NBC triangeluek ere azalera bera dutela ikusten da.
Egileaz: Javier Duoandikoetxea Analisi Matematikoko Katedraduna da UPV/EHUn.